Loại Ký số Biểu tượng số
Ký số La Mã
I
II
III
IV
V
VI
VII
VIII
IX
X
Ký số Ả rập
1
2
3
4
5
6
7
8
9
10
Ký số Trung quốc
-
=
Giá trị
1
2
3
4
5
6
7
8
9
10
Toán đại số dùng chữ cái a-z, A-Z đại diện cho các con số số học từ 0 đến 9. Thí dụ như A = 3 , B = 2 . Các chữ cái đại diện cho các con số số học được gọi là Biến số. Số đại số được phân loai thành các loại số dưới đây
Loai số đại số Định nghỉa Ký hiệu Thí dụ
Số tự nhiên
N
{\displaystyle N}
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle 0,1,2,3,4,5,6,7,8,9}
Số chẳn Mọi số chia hết cho 2
2
n
{\displaystyle 2n}
2
,
4
,
6
,
{\displaystyle 2,4,6,}
Số lẻ Mọi số không chia hết cho 2
2
n
+
1
{\displaystyle 2n+1}
1
,
3
,
5
,
7
,
9
{\displaystyle 1,3,5,7,9}
Số nguyên tố Mọi số chia hết cho 1 và cho chính nó
p
{\displaystyle p}
1
,
3
,
5
,
7
{\displaystyle 1,3,5,7}
Số lũy thừa
a
n
=
a
×
a
×
a
.
.
.
×
a
{\displaystyle a^{n}=a\times a\times a...\times a}
a
n
{\displaystyle a^{n}}
2
3
=
2
×
2
×
2
=
8
{\displaystyle 2^{3}=2\times 2\times 2=8}
Số căn
n
a
{\displaystyle n{\sqrt {a}}}
a
1
n
{\displaystyle a^{\frac {1}{n}}}
n
a
{\displaystyle n{\sqrt {a}}}
a
1
n
{\displaystyle a^{\frac {1}{n}}}
Số log
L
o
g
a
b
=
c
{\displaystyle Log_{a}b=c}
a
c
=
b
{\displaystyle a^{c}=b}
L
o
g
a
b
{\displaystyle Log_{a}b}
L
o
g
10
100
=
2
{\displaystyle Log_{10}100=2}
Số nguyên
I
=
+
I
,
−
I
,
0
{\displaystyle I=+I,-I,0}
I
{\displaystyle I}
+
1
,
−
1
,
0
{\displaystyle +1,-1,0}
Phân số Số có dạng một số trên một số khác
a
b
{\displaystyle {\frac {a}{b}}}
1
2
{\displaystyle {\frac {1}{2}}}
Số thập phân
0.
a
b
c
d
{\displaystyle 0.abcd}
0.5
{\displaystyle 0.5}
Số hửu tỉ
Số vô tỉ
Số phức
Z
=
a
±
j
b
{\displaystyle Z=a\pm jb}
Z
{\displaystyle Z}
2
±
j
3
{\displaystyle 2\pm j3}
Số thực
a
{\displaystyle a}
a
{\displaystyle a}
2
{\displaystyle 2}
Số ảo
j
/
i
=
−
1
{\displaystyle j/i={\sqrt {-1}}}
i
,
j
{\displaystyle i,j}
±
j
3
{\displaystyle \pm j3}
Hằng số Số đại số có giá trị không đổi
c
{\displaystyle c}
π
,
e
{\displaystyle \pi ,e}
Các phép toán đại số thực thi trên các số đại số bao gồm
Toán Ký Hiệu Công Thức Định Nghỉa
Toán cộng
+
{\displaystyle +}
A
+
B
{\displaystyle A+B}
Toán Cộng hai số đại số
Toán trừ
−
{\displaystyle -}
A
−
B
{\displaystyle A-B}
Toán Trừ hai số đại số
Toán nhân
x
{\displaystyle x}
A
×
B
{\displaystyle A\times B}
Toán Nhân hai số đại số
Toán chia
/
{\displaystyle /}
A
/
B
{\displaystyle A/B}
Toán Chia hai số đại số
Toán lũy thừa
a
n
{\displaystyle a^{n}}
a
n
=
a
×
a
×
a
.
.
.
{\displaystyle a^{n}=a\times a\times a...}
Toán tìm tích n lần của chính số nhân
Toán căn
{\displaystyle {\sqrt {}}}
a
=
b
{\displaystyle {\sqrt {a}}=b}
b
n
=
a
{\displaystyle b^{n}=a}
Toán lủy thừa nghịch
Toán log
L
o
g
,
L
n
{\displaystyle Log,Ln}
L
o
g
10
a
=
b
{\displaystyle Log_{10}a=b}
10
b
=
a
{\displaystyle 10^{b}=a}
Toán Toán lủy thừa nghịch của một lủy thừa
Số nguyên
I
=
I
<
0
,
I
=
0
,
I
>
0
{\displaystyle I={I<0,I=0,I>0}}
a
n
=
a
×
a
×
a
×
a
.
.
.
×
a
{\displaystyle a^{n}=a\times a\times a\times a...\times a}
n
a
=
b
{\displaystyle n{\sqrt {a}}=b}
a
=
b
n
{\displaystyle a=b^{n}}
L
o
g
a
b
=
c
{\displaystyle Log_{a}b=c}
a
c
=
b
{\displaystyle a^{c}=b}
Toán Log Công thức
Viết tắc
L
o
g
=
L
o
g
10
{\displaystyle Log=Log_{10}}
L
n
=
L
o
g
2
{\displaystyle Ln=Log_{2}}
Log 1
L
o
g
(
1
)
=
0
{\displaystyle Log(1)=0}
Log lũy thừa
L
o
g
n
(
A
)
n
=
A
{\displaystyle Log_{n}(A)^{n}=A}
Lũy thừa log
B
L
o
g
B
(
A
)
=
A
{\displaystyle B^{Log_{B}(A)}=A}
Log của tích số
L
o
g
(
A
B
)
=
L
o
g
A
+
L
o
g
B
{\displaystyle Log(AB)=LogA+LogB}
Log của thương số
L
o
g
(
A
B
)
=
L
o
g
A
−
L
o
g
B
{\displaystyle Log({\frac {A}{B}})=LogA-LogB}
Log của lủy thừa
L
o
g
(
A
n
)
=
n
L
o
g
A
{\displaystyle Log(A^{n})=nLogA}
Đổi nền log
L
o
g
a
x
=
L
o
g
x
L
o
g
a
{\displaystyle Log_{a}x={\frac {Logx}{Loga}}}
[ sửa ] Số phức được biểu diển như ở dưới đây
Số phức Thuận
Z
{\displaystyle Z}
Nghịch
Z
∗
{\displaystyle Z^{*}}
Biểu diển dưới dạng xy
Z
=
x
+
j
y
{\displaystyle Z=x+jy}
Z
=
x
−
j
y
{\displaystyle Z=x-jy}
Biểu diển dưới dạng Zθ
Z
∠
θ
=
x
2
+
y
2
∠
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle tan^{-1}{\frac {y}{x}}}
Z
∠
θ
=
x
2
+
y
2
∠
−
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle -tan^{-1}{\frac {y}{x}}}
Biểu diển dưới dạng hàm số lượng giác
Z
=
z
(
c
o
s
θ
+
j
s
i
n
θ
)
{\displaystyle Z=z(cos\theta +jsin\theta )}
Z
=
z
(
c
o
s
θ
−
j
s
i
n
θ
)
{\displaystyle Z=z(cos\theta -jsin\theta )}
Biểu diển dưới lũy thừa của e
Z
=
z
e
j
θ
{\displaystyle Z=ze^{j\theta }}
Z
=
z
e
−
j
θ
{\displaystyle Z=ze^{-j\theta }}
Toán số phức được thực thi như sau
Toán Số phức Toán cộng Toán trừ Toán nhân Toán chia
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
Z
=
z
e
j
θ
{\displaystyle Z=ze^{j\theta }}
Z
=
z
e
−
j
θ
{\displaystyle Z=ze^{-j\theta }}
z
(
e
j
θ
+
e
−
j
θ
)
{\displaystyle z(e^{j\theta }+e^{-j\theta })}
z
(
e
j
θ
−
e
−
j
θ
)
{\displaystyle z(e^{j\theta }-e^{-j\theta })}
z
2
{\displaystyle z^{2}}
e
j
2
θ
{\displaystyle e^{j2\theta }}
Định lý Demoive
(
Z
∠
θ
)
n
=
Z
n
∠
n
θ
{\displaystyle (Z\angle \theta )^{n}=Z^{n}\angle n\theta }
Dải Số là một chuổi số có định dạng . Thí dụ
Dải số của các số tự nhiên
1
,
2
,
3
,
4
,
5
,
.
.
.
.
,
n
{\displaystyle 1,2,3,4,5,....,n}
Dải số của các số tự nhiên chẳn
2
,
4
,
6
,
8
,
10
,
.
.
.
,
2
n
{\displaystyle 2,4,6,8,10,...,2n}
Dải số của các số tự nhiên lẻ
1
,
3
,
5
,
7
,
.
.
.
,
2
n
+
1
{\displaystyle 1,3,5,7,...,2n+1}
Chuổi sô Định nghỉa Ký hiệu Thí dụ
Chuổi số
phép toán tìm tổng của một dải số
S
=
∑
{\displaystyle S=\sum }
S
n
=
∑
i
=
1
n
a
i
=
1
+
2
+
⋯
+
n
=
1
+
2
+
3
+
.
.
.
+
n
=
k
(
1
+
n
)
{\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}=1+2+\cdots +n=1+2+3+...+n=k(1+n)}
[ sửa ] Dạng tổng quát
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}
Chứng minh
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
n
2
(
2
a
+
(
n
−
1
)
d
)
{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}
S
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}
S
=
[
a
+
(
n
−
1
)
d
]
+
.
.
.
+
(
n
−
1
)
d
]
+
a
{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}
2
S
=
[
2
a
+
(
n
−
1
)
d
]
n
{\displaystyle 2S=[2a+(n-1)d]n}
S
=
[
2
a
+
(
n
−
1
)
d
]
n
2
{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}
Thí dụ
Dải số cấp số cộng có dạng tổng quát
1
,
2
,
3
,
.
.
.9
{\displaystyle 1,2,3,...9}
Tổng số của dải số
1
+
2
+
3
+
4
+
5
+
.
.
.9
=
50
{\displaystyle 1+2+3+4+5+...9=50}
Cách giải
S
=
(
1
+
9
)
+
(
2
+
8
)
+
(
3
+
7
)
+
(
4
+
6
)
+
(
5
+
5
)
=
10
(
5
)
=
50
{\displaystyle S=(1+9)+(2+8)+(3+7)+(4+6)+(5+5)=10(5)=50}
[ sửa ] Dạng tổng quát
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
∑
k
=
0
∞
(
a
r
k
)
{\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}=\sum _{k=0}^{\infty }(ar^{k})}
Chứng minh
∑
k
=
0
∞
(
a
r
k
)
=
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle \sum _{k=0}^{\infty }(ar^{k})=a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}={\frac {a(1-r^{n})}{1-r}}}
S
=
a
+
a
r
+
a
r
2
+
a
r
3
+
.
.
.
+
a
r
n
−
1
{\displaystyle S=a+ar+ar^{2}+ar^{3}+...+ar^{n-1}}
r
S
=
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
.
.
.
+
a
r
n
{\displaystyle rS=ar+ar^{2}+ar^{3}+ar^{4}+...+ar^{n}}
S
−
r
S
=
a
−
a
r
n
{\displaystyle S-rS=a-ar^{n}}
S
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle S={\frac {a(1-r^{n})}{1-r}}}
S
=
a
1
−
r
{\displaystyle S={\frac {a}{1-r}}}
n
<
1
{\displaystyle n<1}
Thí dụ
1
+
1.1
+
1.1
2
+
1.1
3
=
4
{\displaystyle 1+1.1+1.1^{2}+1.1^{3}=4}
1
+
1.2
+
1.2
2
+
1.2
3
=
1
+
2
+
4
+
8
=
15
{\displaystyle 1+1.2+1.2^{2}+1.2^{3}=1+2+4+8=15}
[ sửa ] Công thức tổng quát lũy thừa n của một tổng
(
x
+
y
)
n
=
∑
r
=
0
n
(
n
r
)
x
r
y
n
−
r
{\displaystyle (x+y)^{n}=\sum _{r=0}^{n}{n \choose r}x^{r}y^{n-r}}
(
x
+
y
)
n
=
(
n
0
)
x
0
y
n
+
(
n
1
)
x
1
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
(
n
n
−
1
)
x
n
−
1
y
1
+
(
n
n
)
x
n
y
0
{\displaystyle (x+y)^{n}={n \choose 0}x^{0}y^{n}+{n \choose 1}x^{1}y^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+{n \choose {n-1}}x^{n-1}y^{1}+{n \choose n}x^{n}y^{0}}
(
x
+
y
)
n
=
y
n
+
n
x
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
n
x
n
−
1
y
+
x
n
{\displaystyle (x+y)^{n}=y^{n}+nxy^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+nx^{n-1}y+x^{n}}
Với
(
n
r
)
=
n
!
r
!
(
n
−
r
)
!
{\displaystyle {n \choose r}={\frac {n!}{r!(n-r)!}}}
Thí dụ
(
x
+
1
)
1
=
{\displaystyle (x+1)^{1}=}
1
x
+
1
{\displaystyle 1x+1}
(
x
+
1
)
2
=
{\displaystyle (x+1)^{2}=}
1
x
2
+
2
x
+
1
{\displaystyle 1x^{2}+2x+1}
(
x
+
1
)
3
=
{\displaystyle (x+1)^{3}=}
1
x
3
+
3
x
2
+
3
x
+
1
{\displaystyle 1x^{3}+3x^{2}+3x+1}
(
x
+
1
)
4
=
{\displaystyle (x+1)^{4}=}
1
x
4
+
4
x
3
+
6
x
2
+
4
x
+
1
{\displaystyle 1x^{4}+4x^{3}+6x^{2}+4x+1}
(
x
+
1
)
5
=
{\displaystyle (x+1)^{5}=}
1
x
5
+
5
x
4
+
10
x
3
+
10
x
2
+
5
x
+
1
{\displaystyle 1x^{5}+5x^{4}+10x^{3}+10x^{2}+5x+1}
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
[ sửa ] Dạng tổng quát
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
f
‴
(
a
)
3
!
(
x
−
a
)
3
+
⋯
=
∑
n
=
0
∞
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}
Tổng chuổi số Fourier đại diện cho tổng chuổi số hàm số sóng sine
s
N
(
x
)
=
A
0
2
+
∑
n
=
1
N
A
n
⋅
sin
(
2
π
n
x
P
+
ϕ
n
)
,
for integer
N
≥
1.
{\displaystyle s_{N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}A_{n}\cdot \sin \left({\tfrac {2\pi nx}{P}}+\phi _{n}\right),\quad {\text{for integer}}\ N\ \geq \ 1.}
[ sửa ]
∑
k
=
0
n
c
=
n
c
{\displaystyle \sum _{k=0}^{n}{c}=nc}
c
{\displaystyle c}
∑
k
=
0
n
k
=
n
(
n
+
1
)
2
{\displaystyle \sum _{k=0}^{n}{k}={\frac {n(n+1)}{2}}}
∑
k
=
0
n
k
2
=
n
(
n
+
1
)
(
2
n
+
1
)
6
{\displaystyle \sum _{k=0}^{n}{k^{2}}={\frac {n(n+1)(2n+1)}{6}}}
∑
k
=
0
n
k
3
=
n
2
(
n
+
1
)
2
4
{\displaystyle \sum _{k=0}^{n}{k^{3}}={\frac {n^{2}(n+1)^{2}}{4}}}
∑
n
=
0
∞
x
n
n
!
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
x
4
4
!
+
⋯
=
e
x
{\displaystyle \sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots =e^{x}}
∑
n
=
1
∞
(
−
1
)
n
+
1
n
x
n
=
x
−
x
2
2
+
x
3
3
−
x
4
4
+
⋯
=
ln
(
1
+
x
)
for
|
x
|
<
1
{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\cdots =\ln(1+x)\quad {\text{ for }}|x|<1}
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
x
2
n
=
1
−
x
2
2
!
+
x
4
4
!
−
⋯
=
cos
(
x
)
for all
x
∈
C
{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots =\cos(x)\quad {\text{ for all }}x\in \mathbb {C} }
Biểu thức Đơn thức Đa thức Đẳng thức Bất đẳng thức
2
x
{\displaystyle 2x}
5
x
y
z
{\displaystyle 5xyz}
2
x
+
5
y
{\displaystyle 2x+5y}
5
x
y
−
2
y
{\displaystyle 5xy-2y}
2
x
=
5
y
{\displaystyle 2x=5y}
5
x
y
=
2
y
{\displaystyle 5xy=2y}
2
x
{\displaystyle 2x}
5
y
{\displaystyle 5y}
5
x
y
{\displaystyle 5xy}
2
y
{\displaystyle 2y}
Hằng đẳng thức Công thức
Bình phương tổng 2 số đại số
(
a
+
b
)
2
=
(
a
+
b
)
(
a
+
b
)
=
a
2
+
a
b
+
a
b
+
b
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=(a+b)(a+b)=a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}}
Bình phương hiệu 2 số đại số
(
a
−
b
)
2
=
(
a
−
b
)
(
a
−
b
)
=
a
2
−
a
b
−
a
b
+
b
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=(a-b)(a-b)=a^{2}-ab-ab+b^{2}=a^{2}-2ab+b^{2}}
Tổng 2 bình phương
a
2
+
b
2
=
(
a
+
b
)
2
−
2
a
b
{\displaystyle a^{2}+b^{2}=(a+b)^{2}-2ab}
a
2
+
b
2
=
(
a
−
b
)
2
+
2
a
b
{\displaystyle a^{2}+b^{2}=(a-b)^{2}+2ab}
Hiệu 2 bình phương
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
Tổng 2 lập phương
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})}
Hiệu 2 lập phương
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}
Hàm số Công thức
Hàm số có dạng tổng quát
f
(
x
,
y
,
z
,
.
.
.
)
{\displaystyle f(x,y,z,...)}
Giá trị hàm số
f
(
x
,
y
,
z
,
.
.
.
)
=
C
{\displaystyle f(x,y,z,...)=C}
Dạng hàm số Công thức Thí dụ
Hàm số tuần hoàn Periodic function
f
(
x
)
=
f
(
x
+
T
)
{\displaystyle f(x)=f(x+T)}
s
i
n
x
=
s
i
n
(
x
+
k
2
π
)
{\displaystyle sinx=sin(x+k2\pi )}
Hàm số chẳn even function
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
Hàm số lẽ odd function
f
(
x
)
=
−
f
(
x
)
{\displaystyle f(x)=-f(x)}
y
(
x
)
=
−
y
(
x
)
{\displaystyle y(x)=-y(x)}
Hàm số nghịch đảo inverse function
f
−
1
(
x
)
=
1
f
(
x
)
{\displaystyle f^{-1}(x)={\frac {1}{f(x)}}}
s
i
n
−
1
x
=
1
s
i
n
x
{\displaystyle sin^{-1}{x}={\frac {1}{sinx}}}
Hàm số trong hàm số composite function
f
(
x
)
=
f
(
g
(
x
)
)
{\displaystyle f(x)=f(g(x))}
Hàm số nhiều biến số parametric function
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Hàm số tương quan/]] recursive function
Với mọi giá trị của x sẻ có một giá trị hàm số của x tương đương . Thí dụ, với hàm số f(x)=x ta có thể thiết lập bảng giá trị tương quan của x và hàm số của x . Khi đặt các giá trị của x và của f(x) trên đồ thị XY ta có thể vẻ được hình đường thẳng có độ góc bằng 1 đi qua điểm gốc ở tọa độ (0,0)
x -2 -1 0 1 2
Hình
F(x)=x -2 -1 0 1 2
Đồ thị hàm số Hình
Thẳng
Cong
Tròn
Lũy thừa
Log
Sin
Cos
Sec
Csc
Tan
Cot
Danh sách các hàm số Công thức
Hàm số đường thẳng
Y
=
Z
X
{\displaystyle Y=ZX}
y
−
y
o
=
Z
(
x
−
x
o
)
{\displaystyle y-y_{o}=Z(x-x_{o})}
y
=
y
o
+
Z
(
x
−
x
o
)
{\displaystyle y=y_{o}+Z(x-x_{o})}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
Z
Z
2
=
X
Z
2
+
Y
Z
2
{\displaystyle {\frac {Z}{Z}}^{2}={\frac {X}{Z}}^{2}+{\frac {Y}{Z}}^{2}}
1
=
c
o
s
2
+
s
i
n
2
{\displaystyle 1=cos^{2}+sin^{2}}
1
=
s
e
c
2
+
t
a
n
2
{\displaystyle 1=sec^{2}+tan^{2}}
1
=
c
s
c
2
+
c
o
t
2
{\displaystyle 1=csc^{2}+cot^{2}}
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
s
i
n
θ
=
Y
Z
{\displaystyle sin\theta ={\frac {Y}{Z}}}
s
e
c
θ
=
1
X
{\displaystyle sec\theta ={\frac {1}{X}}}
c
s
c
θ
=
1
Y
{\displaystyle csc\theta ={\frac {1}{Y}}}
t
a
n
θ
=
Y
X
{\displaystyle tan\theta ={\frac {Y}{X}}}
c
o
t
θ
=
X
Y
{\displaystyle cot\theta ={\frac {X}{Y}}}
y
=
a
x
n
{\displaystyle y=ax^{n}}
y
(
x
)
=
L
o
g
x
{\displaystyle y(x)=Logx}
y
(
x
)
=
a
x
n
+
a
n
−
1
x
n
−
1
+
.
.
.
+
a
0
x
0
{\displaystyle y(x)=ax^{n}+a_{n-1}x^{n-1}+...+a_{0}x^{0}}
Q
(
x
)
=
N
(
x
)
M
(
x
)
−
R
(
x
)
{\displaystyle Q(x)={\frac {N(x)}{M(x)}}-R(x)}
[ sửa ] Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
+
.
.
.
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
+
.
.
.
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}+...=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}+...}
Chứng minh
Khi x=0
f
(
0
)
=
a
0
{\displaystyle f(0)=a_{0}}
f
′
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
4
a
4
x
3
{\displaystyle f^{'}(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+4a_{4}x^{3}}
f
′
(
0
)
=
a
1
{\displaystyle f^{'}(0)=a_{1}}
f
″
(
x
)
=
2
a
2
+
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
a
4
x
2
+
(
5
)
(
4
)
a
5
x
3
{\displaystyle f^{''}(x)=2a_{2}+(3)(2)a_{3}x+(4)(3)a_{4}x^{2}+(5)(4)a_{5}x^{3}}
f
″
(
0
)
=
2
a
2
{\displaystyle f^{''}(0)=2a_{2}}
a
2
=
f
″
(
0
)
2
{\displaystyle a_{2}={\frac {f^{''}(0)}{2}}}
f
‴
(
x
)
=
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
(
2
)
a
4
x
+
(
5
)
(
4
)
(
3
)
a
5
x
2
{\displaystyle f^{'''}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_{5}x^{2}}
f
‴
(
0
)
=
(
3
)
(
2
)
a
3
{\displaystyle f^{'''}(0)=(3)(2)a_{3}}
a
3
=
f
‴
(
0
)
3
!
{\displaystyle a_{3}={\frac {f^{'''}(0)}{3!}}}
a
0
,
a
−
1
,
a
−
2
{\displaystyle a_{0},a-1,a-2}
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}}
f
(
x
)
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
{\displaystyle f(x)=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}}
[ sửa ] Với đường thẳng nghiêng đi qua 2 điểm (xo,yo) - (x,y) dưới đây
Ta có thể tính các loại toán sau
Biến đổi hàm số Biến đổi hàm số cho biết tỉ lệ thay đổi biến số y trên thay đổi biến số x có thể biểu diển bằng công thức toán dưới đây
a
=
Δ
y
Δ
x
=
y
−
y
o
x
−
x
o
{\displaystyle a={\frac {\Delta y}{\Delta x}}={\frac {y-y_{o}}{x-x_{o}}}}
a
=
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
{\displaystyle a={\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}}
Với
Δ
x
=
x
−
x
o
=
(
x
+
Δ
x
)
−
x
{\displaystyle \Delta x=x-x_{o}=(x+\Delta x)-x}
Δ
y
=
y
−
y
o
=
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=y-y_{o}=\Delta f(x)=f(x+\Delta x)-f(x)}
Diện tích dưới hình
s
=
Δ
x
y
+
Δ
x
Δ
y
2
=
Δ
x
[
y
+
Δ
y
2
]
=
Δ
x
[
f
(
x
)
+
Δ
f
(
x
)
2
]
{\displaystyle s=\Delta xy+\Delta x{\frac {\Delta y}{2}}=\Delta x[y+{\frac {\Delta y}{2}}]=\Delta x[f(x)+{\frac {\Delta f(x)}{2}}]}
s
=
Δ
x
[
f
(
x
)
+
Δ
f
(
x
)
2
]
=
Δ
x
2
[
2
f
(
x
)
+
f
(
x
+
Δ
x
)
−
f
(
x
)
]
=
Δ
x
2
[
f
(
x
)
+
f
(
x
+
Δ
x
)
]
{\displaystyle s=\Delta x[f(x)+{\frac {\Delta f(x)}{2}}]={\frac {\Delta x}{2}}[2f(x)+f(x+\Delta x)-f(x)]={\frac {\Delta x}{2}}[f(x)+f(x+\Delta x)]}
Với mọi đường cong bên dưới
Ta có thể tính các loại toán sau
Đạo hàm hàm số đường cong
d
d
x
f
(
x
)
=
f
′
(
x
)
=
lim
Δ
x
→
0
∑
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
∑
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=f^{'}(x)=\lim _{\Delta x\to 0}\sum {\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}\sum {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
Tích phân xác định đường cong
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)}
Tích phân bất định đường cong
∫
f
(
x
)
d
x
=
lim
Δ
x
→
0
∑
(
f
(
x
)
+
Δ
f
(
x
)
2
)
Δ
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)dx=\lim _{\Delta x\rightarrow 0}\sum (f(x)+{\frac {\Delta f(x)}{2}})\Delta x=F(x)+C}
Phương trình có dạng tổng quát
f
(
x
,
y
,
z
,
.
.
.
)
=
0
{\displaystyle f(x,y,z,...)=0}
Quá trình tìm giá trị nghiệm số thỏa mản
[ sửa ] [ sửa ] Ký hiệu
. Thí dụ
. A Đường nối liền giửa 2 điểm tạo từ nhiều đoạn thẳng
[ sửa ]
Định nghỉa Tính chất
Đường thẳng vuông góc
Khi hai đường thẳng cắt nhau tại một điểm tạo nên một góc vuông 90o sẻ tạo ra hai Đường thẳng vuông góc voi nhau
A
B
⊥
C
D
{\displaystyle AB\perp CD}
⊥
{\displaystyle \perp }
o o + 90o = 180o o - Góc B xanho - Góc B đỏ
[ sửa ] Hai đường thẳng không cắt nhau tại bất kỳ điểm nào là đường thẳng song song . Hai đường thẳng song song là hai đường thẳng không có điểm chung . Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song
A ------------- B
C ------------- D Ký hiệu đường thẳng song song
/
/
{\displaystyle //}
AB // CD Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau;
Hai góc đồng vị bằng nhau;
Hai góc trong cùng phía bù nhau.
[ sửa ] Tương quan giửa góc và cạnh trong tam giác vuông Pythagore
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
s
i
n
θ
=
Y
Z
{\displaystyle sin\theta ={\frac {Y}{Z}}}
s
e
c
θ
=
1
X
{\displaystyle sec\theta ={\frac {1}{X}}}
c
s
c
θ
=
1
Y
{\displaystyle csc\theta ={\frac {1}{Y}}}
t
a
n
θ
=
Y
X
{\displaystyle tan\theta ={\frac {Y}{X}}}
c
o
t
θ
=
X
Y
{\displaystyle cot\theta ={\frac {X}{Y}}}
Độ dài các cạnh
X
=
Y
Z
=
Z
c
o
s
θ
=
x
−
x
o
=
Δ
x
{\displaystyle X={\frac {Y}{Z}}=Zcos\theta =x-x_{o}=\Delta x}
Y
=
Z
X
=
Z
s
i
n
θ
=
y
−
y
o
=
Δ
y
{\displaystyle Y=ZX=Zsin\theta =y-y_{o}=\Delta y}
Z
=
Y
X
=
t
a
n
θ
=
y
−
y
o
x
−
x
o
=
Δ
y
Δ
x
{\displaystyle Z={\frac {Y}{X}}=tan\theta ={\frac {y-y_{o}}{x-x_{o}}}={\frac {\Delta y}{\Delta x}}}
θ
=
t
a
n
−
1
Z
=
t
a
n
−
1
Y
X
{\displaystyle \theta =tan^{-1}Z=tan^{-1}{\frac {Y}{X}}}
Phương trình đường thẳng nghiêng
Z
∠
θ
=
X
2
+
Y
2
∠
t
a
n
−
1
Y
X
{\displaystyle Z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle tan^{-1}{\frac {Y}{X}}}
Y
=
Z
X
{\displaystyle Y=ZX}
Từ trên
X
=
Y
Z
=
y
−
y
o
Z
{\displaystyle X={\frac {Y}{Z}}={\frac {y-y_{o}}{Z}}}
y
=
y
o
+
Z
X
{\displaystyle y=y_{o}+ZX}
y
o
=
y
−
Z
X
{\displaystyle y_{o}=y-ZX}
Diện tích dưới hình
S
=
X
(
y
o
+
Y
2
)
=
X
(
y
o
+
Z
X
2
)
=
X
(
y
−
Z
X
2
)
{\displaystyle S=X(y_{o}+{\frac {Y}{2}})=X(y_{o}+{\frac {ZX}{2}})=X(y-{\frac {ZX}{2}})}
S
=
(
y
−
y
o
Z
)
(
2
y
o
+
y
−
y
o
2
)
=
y
2
−
y
o
2
2
Z
{\displaystyle S=({\frac {y-y_{o}}{Z}})({\frac {2y_{o}+y-y_{o}}{2}})={\frac {y^{2}-y_{o}^{2}}{2Z}}}
Vector đại diện cho một đường thẳng có hướng và có một độ dài . Vectơ có ký hiệu → . Thí dụ, Vector
A
B
→
{\displaystyle {\vec {AB}}}
Mọi vector A đều có thể biểu diển bằng cường độ vector nhân với vector đơn vị như dưới đây
A
→
=
A
a
→
{\displaystyle {\vec {A}}=A{\vec {a}}}
Với
A
→
{\displaystyle {\vec {A}}}
A
→
=
A
{\displaystyle {\vec {A}}=A}
A
→
=
a
→
{\displaystyle {\vec {A}}={\vec {a}}}
A
=
A
→
a
{\displaystyle A={\frac {\vec {A}}{a}}}
Vector 1 đơn vị
a
→
=
A
→
a
{\displaystyle {\vec {a}}={\frac {\vec {A}}{a}}}
Vector đường thẳng ngang
X
→
=
X
i
→
{\displaystyle {\vec {X}}=X{\vec {i}}}
Vector đường thẳng dọc
Y
→
=
Y
j
→
{\displaystyle {\vec {Y}}=Y{\vec {j}}}
Vector đường thẳng nghiêng
Z
→
=
Z
k
→
{\displaystyle {\vec {Z}}=Z{\vec {k}}}
Vector đường tròn
R
→
=
R
r
→
=
X
→
+
Y
→
=
X
i
→
+
Y
j
→
{\displaystyle {\vec {R}}=R{\vec {r}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}}
Phép cộng hai vectơ : tổng của hai vectơ
A
B
→
{\displaystyle {\overrightarrow {AB}}}
C
D
→
{\displaystyle {\overrightarrow {CD}}}
di chuyển vectơ
C
D
→
{\displaystyle {\overrightarrow {CD}}}
C
D
→
{\displaystyle {\overrightarrow {CD}}}
A
B
→
{\displaystyle {\overrightarrow {AB}}}
C
≡
B
{\displaystyle C\equiv B}
A
D
→
{\displaystyle {\overrightarrow {AD}}}
di chuyển vectơ
C
D
→
{\displaystyle {\overrightarrow {CD}}}
A
B
→
{\displaystyle {\overrightarrow {AB}}}
A
B
→
{\displaystyle {\overrightarrow {AB}}}
C
D
→
{\displaystyle {\overrightarrow {CD}}}
Tính chất Vectơ Công thức
Tính chất giao hoán
a
→
+
b
→
=
b
→
+
a
→
{\displaystyle {\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}}
Tính chất kết hợp
(
a
→
+
b
→
)
+
c
→
=
a
→
+
(
b
→
+
c
→
)
{\displaystyle ({\vec {a}}+{\vec {b}})+{\vec {c}}={\vec {a}}+({\vec {b}}+{\vec {c}})}
Tính chất của vectơ-không
a
→
+
0
→
=
0
→
+
a
→
=
a
→
{\displaystyle {\vec {a}}+{\vec {0}}={\vec {0}}+{\vec {a}}={\vec {a}}}
Với 3 điểm A, B, C thẳng hàng ta có:
A
B
→
+
B
C
→
=
A
C
→
{\displaystyle {\vec {AB}}+{\vec {BC}}={\vec {AC}}}
I là trung điểm đoạn thẳng AB
⇔
A
I
→
+
B
I
→
=
0
→
{\displaystyle \Leftrightarrow {\vec {AI}}+{\vec {BI}}={\vec {0}}}
G là trọng tâm
△
A
B
C
{\displaystyle \vartriangle ABC}
⇔
G
A
→
+
G
B
→
+
G
C
→
=
0
→
{\displaystyle \Leftrightarrow {\vec {GA}}+{\vec {GB}}+{\vec {GC}}={\vec {0}}}
Với hai vectơ bất kì, với hằng số h và k, ta có
k
(
a
→
+
b
→
)
=
k
a
→
+
k
b
→
{\displaystyle k({\vec {a}}+{\vec {b}})=k{\vec {a}}+k{\vec {b}}}
(
h
+
k
)
a
→
=
h
a
→
+
k
a
→
{\displaystyle (h+k){\vec {a}}=h{\vec {a}}+k{\vec {a}}}
h
(
k
a
→
)
=
(
h
k
)
a
→
{\displaystyle h(k{\vec {a}})=(hk){\vec {a}}}
1.
a
→
=
a
→
{\displaystyle 1.{\vec {a}}={\vec {a}}}
(
−
1
)
.
a
→
=
−
a
→
{\displaystyle (-1).{\vec {a}}=-{\vec {a}}}
Tích vô hướng của hai vectơ A = [A 1 , A 2 ,.. ., A n và B = [B 1 , B 2 ,.. ., B n được định nghĩa như sau
A
⋅
B
=
∑
i
=
1
n
A
i
B
i
=
A
1
B
1
+
A
2
B
2
+
⋯
+
A
n
B
n
{\displaystyle \mathbf {A} \cdot \mathbf {B} =\sum _{i=1}^{n}A_{i}B_{i}=A_{1}B_{1}+A_{2}B_{2}+\cdots +A_{n}B_{n}}
A
⋅
B
=
‖
A
‖
‖
B
‖
cos
(
θ
)
,
{\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\ \|\mathbf {B} \|\cos(\theta ),}
A và B .Trường hợp đặc biệt,
Nếu A và B trực giao thì góc giữa chúng là 90°, do đó:
A
⋅
B
=
0.
{\displaystyle \mathbf {A} \cdot \mathbf {B} =0.}
Nếu chúng cùng hướng thì góc giữa chúng là 0°, do đó:
A
⋅
B
=
‖
A
‖
‖
B
‖
{\displaystyle \mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\,\left\|\mathbf {B} \right\|}
Suy ra tích vô hướng của vectơ A và chính nó là:
A
⋅
A
=
‖
A
‖
2
,
{\displaystyle \mathbf {A} \cdot \mathbf {A} =\left\|\mathbf {A} \right\|^{2},}
ta có:
‖
A
‖
=
A
⋅
A
,
{\displaystyle \left\|\mathbf {A} \right\|={\sqrt {\mathbf {A} \cdot \mathbf {A} }},}
là khoảng cách Euclid của vectơ, luôn có giá trị dương khi A khác 0 .
A = [A 1 , A 2 ,.. ., A n
‖
A
‖
=
∑
k
=
1
n
A
k
2
{\displaystyle \left\|\mathbf {A} \right\|={\sqrt {\sum _{k=1}^{n}A_{k}^{2}}}}
Cho a , b , và c là các vectơ và r là đại lượng vô hướng , tích vô hướng thỏa mãn các tính chất sau:.
Giao hoán :
a
⋅
b
=
b
⋅
a
,
{\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} ,}
được suy ra từ định nghĩa (θ góc giữa a và b ):
a
⋅
b
=
‖
a
‖
‖
b
‖
cos
θ
=
‖
b
‖
‖
a
‖
cos
θ
=
b
⋅
a
.
{\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta =\left\|\mathbf {b} \right\|\left\|\mathbf {a} \right\|\cos \theta =\mathbf {b} \cdot \mathbf {a} .}
Phân phối cho phép cộng vectơ:
a
⋅
(
b
+
c
)
=
a
⋅
b
+
a
⋅
c
.
{\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}
Dạng song tuyến
a
⋅
(
r
b
+
c
)
=
r
(
a
⋅
b
)
+
(
a
⋅
c
)
.
{\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).}
Phép nhân vô hướng :
(
c
1
a
)
⋅
(
c
2
b
)
=
c
1
c
2
(
a
⋅
b
)
.
{\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=c_{1}c_{2}(\mathbf {a} \cdot \mathbf {b} ).}
Không có tính kết hợp bởi vì tích vô hướng giữa đại lượng vô hướng (a ⋅ b ) và vectơ (c ) không tồn tại, tức là biểu thức cho tính kết hợp: (a ⋅ b ) ⋅ c or a ⋅ (b ⋅ c ) là không hợp lệ.Trực giao :Hai vectơ khác vectơ không: a và b trực giao khi và chỉ khi a ⋅ b = 0
Hai vectơ trực giao trong không gian Euclid còn được gọi là vuông góc . Không có tính khử :
Tính khử cho phép nhân của các số được định nghĩa như sau: nếu
ab = ac b luôn luôn bằng c nếu a khác 0. Tích vô hướng không tuân theo tính khử:Nếu a ⋅ b = a ⋅ c a ≠ 0 a ⋅ (b − c ) = 0phân phối ; suy ra a trực giao với (b − c ) , tức là (b − c ) ≠ 0 b ≠ c Quy tắc đạo hàm tích: Nếu a và b là hàm số , thì đạo hàm ca ⋅ b a ′ ⋅ b + a ⋅ b ′
Tam giác có cạnh vectơ a and b , và góc giữa 2 vectơ là θ . Hai vectơ a và b có góc giữa hai vectơ là θ (như trong hình bên phải) tạo thành một tam giác có cạnh thứ ba là c = a − b c và chính nó là Định lý cos :
c
⋅
c
=
(
a
−
b
)
⋅
(
a
−
b
)
=
a
⋅
a
−
a
⋅
b
−
b
⋅
a
+
b
⋅
b
=
a
2
−
a
⋅
b
−
a
⋅
b
+
b
2
=
a
2
−
2
a
⋅
b
+
b
2
c
2
=
a
2
+
b
2
−
2
a
b
cos
θ
{\displaystyle {\begin{aligned}\mathbf {c} \cdot \mathbf {c} &=(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\\&=\mathbf {a} \cdot \mathbf {a} -\mathbf {a} \cdot \mathbf {b} -\mathbf {b} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} \\&=a^{2}-\mathbf {a} \cdot \mathbf {b} -\mathbf {a} \cdot \mathbf {b} +b^{2}\\&=a^{2}-2\mathbf {a} \cdot \mathbf {b} +b^{2}\\c^{2}&=a^{2}+b^{2}-2ab\cos \theta \\\end{aligned}}}
Minh họa kết quả phép nhân vectơ trong hệ tọa độ bên phải
Xác định hướng của tích vectơ bằng Quy tắc bàn tay phải . Phép nhân vectơ của vectơ a và b được ký hiệu là a × b hay
[
a
→
,
b
→
]
{\displaystyle [{\vec {a}},{\vec {b}}]}
a
×
b
=
n
^
|
a
|
|
b
|
sin
θ
{\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {\hat {n}} \left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \theta }
với θ là góc giữa a và b (0° ≤ θ ≤ 180°) nằm trên mặt phẳng chứa a và b , và n là vectơ đơn vị vuông góc với a và b .
Thực tế có hai vectơ n thỏa mãn điều kiện vuông góc với a và b (khi a và b không cùng phương), vì nếu n vuông góc với a và b thì -n cũng vậy.
Việc chọn hướng của véctơ n phụ thuộc vào hệ tọa độ tuân theo quy tắc bàn tay trái hay quy tắc bàn tay phải . (a , b , a × b ) tuân cùng quy tắc với hệ tọa độ đang sử dụng để xác định các vectơ.
Vì kết quả phụ thuộc vào quy ước hệ tọa độ, nó được gọi là giả vectơ . May mắn là trong các hiện tượng tự nhiên, nhân vectơ luôn đi theo cặp đối chiều nhau, nên kết quả cuối cùng không phụ thuộc lựa chọn hệ tọa độ.
hệ trục tọa độ Oxyz, cho
n
1
→
=
(
A
1
,
B
1
,
C
1
)
{\displaystyle {\vec {n_{1}}}=(A_{1},B_{1},C_{1})}
n
2
→
=
(
A
2
,
B
2
,
C
2
)
{\displaystyle {\vec {n_{2}}}=(A_{2},B_{2},C_{2})}
[
n
1
→
,
n
2
→
]
=
(
|
B
1
C
1
B
2
C
2
|
,
|
C
1
A
1
C
2
A
2
|
,
|
A
1
B
1
A
2
B
2
|
)
{\displaystyle [{\vec {n_{1}}},{\vec {n_{2}}}]=({\begin{vmatrix}B_{1}&C_{1}\\B_{2}&C_{2}\end{vmatrix}},{\begin{vmatrix}C_{1}&A_{1}\\C_{2}&A_{2}\end{vmatrix}},{\begin{vmatrix}A_{1}&B_{1}\\A_{2}&B_{2}\end{vmatrix}})}
Vector chuyển động thẳng hàng ngang
X
→
=
X
i
→
{\displaystyle {\vec {X}}=X{\vec {i}}}
Vector chuyển động thẳng hàng dọc
Y
→
=
Y
j
→
{\displaystyle {\vec {Y}}=Y{\vec {j}}}
Vector chuyển động thẳng hàng nghiêng
Z
→
=
Z
k
→
{\displaystyle {\vec {Z}}=Z{\vec {k}}}
Vector chuyển động tròn
R
→
=
R
r
→
=
X
→
+
Y
→
{\displaystyle {\vec {R}}=R{\vec {r}}={\vec {X}}+{\vec {Y}}}
Vector chuyển động thẳng hàng ngang
i
→
=
X
→
X
{\displaystyle {\vec {i}}={\frac {\vec {X}}{X}}}
Vector chuyển động thẳng hàng dọc
j
→
=
Y
→
Y
{\displaystyle {\vec {j}}={\frac {\vec {Y}}{Y}}}
Vector chuyển động thẳng hàng nghiêng
k
→
=
Z
→
Z
{\displaystyle {\vec {k}}={\frac {\vec {Z}}{Z}}}
Vector chuyển động tròn
r
→
=
R
→
R
{\displaystyle {\vec {r}}={\frac {\vec {R}}{R}}}
Cường độ Vector chuyển động thẳng hàng ngang
X
=
X
→
i
→
{\displaystyle X={\frac {\vec {X}}{\vec {i}}}}
Cường độ Vector chuyển động thẳng hàng dọc
Y
=
Y
→
j
→
{\displaystyle Y={\frac {\vec {Y}}{\vec {j}}}}
Cường độ Vector chuyển động thẳng hàng nghiêng
Z
=
Z
→
k
→
{\displaystyle Z={\frac {\vec {Z}}{\vec {k}}}}
Cường độ Vector chuyển động tròn
R
=
R
→
r
→
{\displaystyle R={\frac {\vec {R}}{\vec {r}}}}
Chuyển Động s v a
Cong
s
(
t
)
{\displaystyle s(t)}
d
d
t
s
(
t
)
{\displaystyle {\frac {d}{dt}}s(t)}
d
2
d
t
2
s
(
t
)
{\displaystyle {\frac {d^{2}}{dt^{2}}}s(t)}
X
→
=
X
i
→
{\displaystyle {\vec {X}}=X{\vec {i}}}
d
d
t
X
→
=
d
X
d
t
i
→
=
v
x
i
→
{\displaystyle {\frac {d}{dt}}{\vec {X}}={\frac {dX}{dt}}{\vec {i}}=v_{x}{\vec {i}}}
d
2
d
t
2
X
→
=
d
2
X
d
t
2
i
→
=
a
x
i
→
{\displaystyle {\frac {d^{2}}{dt^{2}}}{\vec {X}}={\frac {d^{2}X}{dt^{2}}}{\vec {i}}=a_{x}{\vec {i}}}
Y
→
=
Y
j
→
{\displaystyle {\vec {Y}}=Y{\vec {j}}}
d
d
t
Y
→
=
d
Y
d
t
j
→
=
v
y
j
→
{\displaystyle {\frac {d}{dt}}{\vec {Y}}={\frac {dY}{dt}}{\vec {j}}=v_{y}{\vec {j}}}
d
2
d
t
2
Y
→
=
d
2
Y
d
t
2
j
→
=
a
y
j
→
{\displaystyle {\frac {d^{2}}{dt^{2}}}{\vec {Y}}={\frac {d^{2}Y}{dt^{2}}}{\vec {j}}=a_{y}{\vec {j}}}
Z
→
=
Z
k
→
{\displaystyle {\vec {Z}}=Z{\vec {k}}}
d
d
t
Z
→
=
d
Z
d
t
k
→
=
v
z
k
→
{\displaystyle {\frac {d}{dt}}{\vec {Z}}={\frac {dZ}{dt}}{\vec {k}}=v_{z}{\vec {k}}}
d
2
d
t
2
Z
→
=
d
2
Z
d
t
2
k
→
=
a
z
k
→
{\displaystyle {\frac {d^{2}}{dt^{2}}}{\vec {Z}}={\frac {d^{2}Z}{dt^{2}}}{\vec {k}}=a_{z}{\vec {k}}}
R
→
=
R
r
→
{\displaystyle {\vec {R}}=R{\vec {r}}}
d
d
t
R
→
{\displaystyle {\frac {d}{dt}}{\vec {R}}}
R
d
d
t
r
→
+
r
→
d
d
t
R
=
R
d
d
t
r
→
{\displaystyle R{\frac {d}{dt}}{\vec {r}}+{\vec {r}}{\frac {d}{dt}}R=R{\frac {d}{dt}}{\vec {r}}}
d
2
d
t
2
R
→
{\displaystyle {\frac {d^{2}}{dt^{2}}}{\vec {R}}}
R
d
2
d
t
2
r
→
+
r
→
d
2
d
t
2
R
=
R
d
2
d
t
2
r
→
{\displaystyle R{\frac {d^{2}}{dt^{2}}}{\vec {r}}+{\vec {r}}{\frac {d^{2}}{dt^{2}}}R=R{\frac {d^{2}}{dt^{2}}}{\vec {r}}}
R
→
=
X
→
+
Y
→
{\displaystyle {\vec {R}}={\vec {X}}+{\vec {Y}}}
d
d
t
R
→
=
d
d
t
(
X
→
+
Y
→
)
{\displaystyle {\frac {d}{dt}}{\vec {R}}={\frac {d}{dt}}({\vec {X}}+{\vec {Y}})}
d
X
d
t
i
→
+
d
Y
d
t
j
→
=
v
x
i
→
+
v
y
j
→
{\displaystyle {\frac {dX}{dt}}{\vec {i}}+{\frac {dY}{dt}}{\vec {j}}=v_{x}{\vec {i}}+v_{y}{\vec {j}}}
d
2
d
t
2
R
→
=
d
2
d
t
2
(
X
→
+
Y
→
)
{\displaystyle {\frac {d^{2}}{dt^{2}}}{\vec {R}}={\frac {d^{2}}{dt^{2}}}({\vec {X}}+{\vec {Y}})}
d
2
X
d
t
2
i
→
+
d
2
Y
d
t
2
j
→
=
a
x
i
→
+
a
y
j
→
{\displaystyle {\frac {d^{2}X}{dt^{2}}}{\vec {i}}+{\frac {d^{2}Y}{dt^{2}}}{\vec {j}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}}
Khi hai đường thẳng cắt nhau tại một điểm sẽ tạo ra một góc giữa hai đường thẳng
Ký hiệu
∠
{\displaystyle \angle }
Đơn vị
1
r
a
d
=
180
o
π
{\displaystyle 1rad={\frac {180^{o}}{\pi }}}
1
o
=
π
180
o
{\displaystyle 1^{o}={\frac {\pi }{180^{o}}}}
Thí dụ
∠
A
=
30
0
=
π
6
r
a
d
{\displaystyle \angle A=30^{0}={\frac {\pi }{6}}rad}
Góc Hình Định nghỉa
Góc nhọn
Góc nhọn là góc nhỏ hơn 90°
Góc vuông
Góc vuông là góc bằng 90° (1/4 vòng tròn);
Góc tù
Góc tù là góc lớn hơn 90° nhưng nhỏ hơn 180°
Góc bẹt
Góc bẹt là góc 180° (1/2 vòng tròn).
Góc phản
Góc phản là góc lớn hơn 180° nhưng nhỏ hơn 360°
Góc đầy
Góc đầy là góc bằng 360° (toàn bộ vòng tròn).
Một tam giác với các thành phần trong định lý sin 3 điểm .
A
,
B
,
C
{\displaystyle A,B,C}
3 cạnh .
A
B
,
B
C
,
C
A
{\displaystyle AB,BC,CA}
3 góc .
∠
A
,
∠
B
,
∠
C
{\displaystyle \angle A,\angle B,\angle C}
[ sửa ]
Chu vi
Diện tích
Thể tích
a
+
b
+
c
{\displaystyle a+b+c}
b
a
2
{\displaystyle {\frac {ba}{2}}}
a
b
h
2
{\displaystyle ab{\frac {h}{2}}}
Trong lượng giác , định lý sin (hay định luật sin , công thức sin ) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}\!}
trong đó a , b , c là chiều dài các cạnh, và A , B , C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:
sin
A
a
=
sin
B
b
=
sin
C
c
.
{\displaystyle {\frac {\sin A}{a}}\,=\,{\frac {\sin B}{b}}\,=\,{\frac {\sin C}{c}}.\!}
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,}
b
2
=
a
2
+
c
2
−
2
a
c
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta \,}
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}
Tam giác vuông là một loại tam giác có 2 cạnh vuông góc với nhau cắt nhau tại một điểm tạo nên một góc vuông bằng
90
o
{\displaystyle 90^{o}}
c - Cạnh huyền
a - Cạnh đối
b - Cạnh kề
Tam giác có 2 cạnh vuông góc với nhau tạo ra một góc vuông 90o
∠
C
=
90
o
{\displaystyle \angle C=90^{o}}
A
C
¯
⊥
C
B
¯
{\displaystyle {\overline {AC}}\perp {\overline {CB}}}
[ sửa ] Tam giác có 1 góc vuông là tam giác vuông
Tam giác có 2 góc nhọn phụ nhau là tam giác vuông
Tam giác có bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh kia là tam giác vuông (định lý Pytago đảo)
Tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy là tam giác vuông
Tam giác nội tiếp đường tròn có 1 cạnh là đường kính thì tam giác đó vuông
Tam giác có cạnh đối diện góc 30° bằng một nửa một cạnh khác trong tam giác thì tam giác đó vuông. Định lý Pytago phát biểu rằng:
Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này . Nó được thể hiện bằng phương trình
a
2
+
b
2
=
c
2
{\displaystyle \displaystyle a^{2}+b^{2}=c^{2}}
Trong đó, c là chiều dài của cạnh huyền và a và b là chiều dài của hai cạnh còn lại.
Tương quan các cạnh và góc
Hàm số góc lượng giác Tỉ lệ cạnh Đồ thị
Cosine
X
Z
=
cos
θ
{\displaystyle {\frac {X}{Z}}=\cos \theta }
Sine
Y
Z
=
sin
θ
{\displaystyle {\frac {Y}{Z}}=\sin \theta }
Cosine
1
X
=
sec
θ
{\displaystyle {\frac {1}{X}}=\sec \theta }
Cosecant
1
Y
=
csc
θ
{\displaystyle {\frac {1}{Y}}=\csc \theta }
Tangent
Y
X
=
tan
θ
{\displaystyle {\frac {Y}{X}}=\tan \theta }
Cotangent
X
Y
=
cot
θ
{\displaystyle {\frac {X}{Y}}=\cot \theta }
[ sửa ]
Hàm số cạnh
Độ dài cạnh ngang
X
=
Y
Z
{\displaystyle X={\frac {Y}{Z}}}
x
−
x
o
{\displaystyle x-x_{o}}
Δ
x
{\displaystyle \Delta x}
Z
cos
θ
{\displaystyle Z\cos \theta }
Độ dài cạnh dọc
Y
=
Z
X
{\displaystyle Y=ZX}
y
−
y
o
{\displaystyle y-y_{o}}
Δ
y
{\displaystyle \Delta y}
Z
sin
θ
{\displaystyle Z\sin \theta }
Độ dóc
Z
=
Y
X
{\displaystyle Z={\frac {Y}{X}}}
y
−
y
o
x
−
x
o
{\displaystyle {\frac {y-y_{o}}{x-x_{o}}}}
Δ
y
Δ
x
{\displaystyle {\frac {\Delta y}{\Delta x}}}
T
a
n
θ
{\displaystyle Tan\theta }
Độ nghiêng
θ
=
tan
−
1
Z
{\displaystyle \theta =\tan ^{-1}Z}
θ
=
tan
−
1
Y
X
{\displaystyle \theta =\tan ^{-1}{\frac {Y}{X}}}
Vector đương thẳng ngang
X
→
=
x
i
→
{\displaystyle {\vec {X}}=x{\vec {i}}}
(
x
−
x
o
)
i
→
{\displaystyle (x-x_{o}){\vec {i}}}
Z
cos
θ
i
→
{\displaystyle Z\cos \theta {\vec {i}}}
Vector đương thẳng dọc
Y
→
=
y
i
→
{\displaystyle {\vec {Y}}=y{\vec {i}}}
(
y
−
y
o
)
i
→
{\displaystyle (y-y_{o}){\vec {i}}}
Z
sin
θ
i
→
{\displaystyle Z\sin \theta {\vec {i}}}
Vector đương thẳng nghiêng
Z
→
=
z
k
→
{\displaystyle {\vec {Z}}=z{\vec {k}}}
(
z
−
z
o
)
k
→
{\displaystyle (z-z_{o}){\vec {k}}}
Hàm số Đường thẳng nghiêng ở độ dóc Z
Y
=
Z
X
{\displaystyle Y=ZX}
y
=
y
o
+
Z
(
x
−
x
o
)
{\displaystyle y=y_{o}+Z(x-x_{o})}
Z
∠
θ
=
X
2
+
Y
2
∠
T
a
n
−
1
Y
X
{\displaystyle Z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle Tan^{-1}{\frac {Y}{X}}}
s
=
X
(
y
o
+
Y
2
)
=
X
(
y
o
+
Z
X
2
)
=
X
(
y
−
Z
X
2
)
=
y
2
−
y
o
2
2
Z
{\displaystyle s=X(y_{o}+{\frac {Y}{2}})=X(y_{o}+{\frac {ZX}{2}})=X(y-{\frac {ZX}{2}})={\frac {y^{2}-y_{o}^{2}}{2Z}}}
[ sửa ] 6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông
Hàm số lượng giác cơ bản
cos
x
{\displaystyle \cos x}
sin
x
{\displaystyle \sin x}
tan
x
{\displaystyle \tan x}
cot
x
{\displaystyle \cot x}
sec
x
{\displaystyle \sec x}
csc
x
{\displaystyle \csc x}
b
c
{\displaystyle {\frac {b}{c}}}
a
c
{\displaystyle {\frac {a}{c}}}
a
b
{\displaystyle {\frac {a}{b}}}
b
a
{\displaystyle {\frac {b}{a}}}
1
b
{\displaystyle {\frac {1}{b}}}
1
a
{\displaystyle {\frac {1}{a}}}
sin
(
x
)
=
sin
(
x
+
2
k
π
)
{\displaystyle \sin(x)=\sin(x+2k\pi )\,}
sin
(
−
x
)
=
−
sin
(
x
)
{\displaystyle \sin(-x)=-\sin(x)\,}
sin
(
x
)
=
cos
(
π
2
−
x
)
{\displaystyle \sin(x)=\cos \left({\frac {\pi }{2}}-x\right)}
cos
(
x
)
=
cos
(
x
+
2
k
π
)
{\displaystyle \cos(x)=\cos(x+2k\pi )\,}
cos
(
−
x
)
=
cos
(
x
)
{\displaystyle \cos(-x)=\;\cos(x)\,}
cos
(
x
)
=
sin
(
π
2
−
x
)
{\displaystyle \cos(x)=\sin \left({\frac {\pi }{2}}-x\right)}
tan
(
x
)
=
tan
(
x
+
k
π
)
{\displaystyle \tan(x)=\tan(x+k\pi )\,}
tan
(
−
x
)
=
−
tan
(
x
)
{\displaystyle \tan(-x)=-\tan(x)\,}
tan
(
x
)
=
cot
(
π
2
−
x
)
{\displaystyle \tan(x)=\cot \left({\frac {\pi }{2}}-x\right)}
cot
(
−
x
)
=
−
cot
(
x
)
{\displaystyle \cot(-x)=-\cot(x)\,}
a
sin
x
+
b
cos
x
=
a
2
+
b
2
⋅
sin
(
x
+
φ
)
{\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )}
với
φ
=
{
a
r
c
t
a
n
(
b
/
a
)
,
n
e
^
´
u
a
≥
0
;
π
+
a
r
c
t
a
n
(
b
/
a
)
,
n
e
^
´
u
a
<
0.
{\displaystyle \varphi =\left\{{\begin{matrix}{\rm {arctan}}(b/a),&&{\mbox{n}}{\acute {\hat {\mbox{e}}}}{\mbox{u}}\ a\geq 0;\;\\\pi +{\rm {arctan}}(b/a),&&{\mbox{n}}{\acute {\hat {\mbox{e}}}}{\mbox{u}}\ a<0.\;\end{matrix}}\right.\;}
sin
(
2
x
)
=
2
sin
(
x
)
cos
(
x
)
{\displaystyle \sin(2x)=2\sin(x)\cos(x)\,}
cos
(
2
x
)
=
cos
2
(
x
)
−
sin
2
(
x
)
=
2
cos
2
(
x
)
−
1
=
1
−
2
sin
2
(
x
)
{\displaystyle \cos(2x)=\cos ^{2}(x)-\sin ^{2}(x)=2\cos ^{2}(x)-1=1-2\sin ^{2}(x)\,}
tan
(
2
x
)
=
2
tan
(
x
)
1
−
tan
2
(
x
)
{\displaystyle \tan(2x)={\frac {2\tan(x)}{1-\tan ^{2}(x)}}}
sin
(
3
x
)
=
3
sin
(
x
)
−
4
sin
3
(
x
)
{\displaystyle \sin(3x)=3\sin(x)-4\sin ^{3}(x)}
cos
(
3
x
)
=
4
cos
3
(
x
)
−
3
cos
(
x
)
{\displaystyle \cos(3x)=4\cos ^{3}(x)-3\cos(x)}
Nếu Tn là đa thức Chebyshev bậc n thì
cos
(
n
x
)
=
T
n
(
cos
(
x
)
)
.
{\displaystyle \cos(nx)=T_{n}(\cos(x)).\,}
công thức de Moivre:
cos
(
n
x
)
+
i
sin
(
n
x
)
=
(
cos
(
x
)
+
i
sin
(
x
)
)
n
{\displaystyle \cos(nx)+i\sin(nx)=(\cos(x)+i\sin(x))^{n}\,}
Hàm hạt nhân Dirichlet Dn(x) sẽ xuất hiện trong các công thức sau:
1
+
2
cos
(
x
)
+
2
cos
(
2
x
)
+
2
cos
(
3
x
)
+
⋯
+
2
cos
(
n
x
)
{\displaystyle 1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)\;}
=
sin
(
(
n
+
1
2
)
x
)
sin
(
x
/
2
)
{\displaystyle ={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}\;}
Hay theo công thức hồi quy:
sin
(
n
x
)
=
2
sin
(
(
n
−
1
)
x
)
cos
(
x
)
−
sin
(
(
n
−
2
)
x
)
{\displaystyle \sin(nx)=2\sin((n-1)x)\cos(x)-\sin((n-2)x)}
cos
(
n
x
)
=
2
cos
(
(
n
−
1
)
x
)
cos
(
x
)
−
cos
(
(
n
−
2
)
x
)
{\displaystyle \cos(nx)=2\cos((n-1)x)\cos(x)-\cos((n-2)x)}
cos
(
x
2
)
=
±
1
+
cos
(
x
)
2
{\displaystyle \cos \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(x)}{2}}}}
sin
(
x
2
)
=
±
1
−
cos
(
x
)
2
{\displaystyle \sin \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(x)}{2}}}}
tan
(
x
2
)
=
sin
(
x
/
2
)
cos
(
x
/
2
)
=
±
1
−
cos
x
1
+
cos
x
.
{\displaystyle \tan \left({\frac {x}{2}}\right)={\sin(x/2) \over \cos(x/2)}=\pm \,{\sqrt {1-\cos x \over 1+\cos x}}.\qquad \qquad }
x , rồi dùng định lý Pytago để đơn giản hóa:
tan
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
=
±
1
−
cos
2
x
(
1
+
cos
x
)
2
{\displaystyle \tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1+\cos x) \over (1+\cos x)(1+\cos x)}}=\pm \,{\sqrt {1-\cos ^{2}x \over (1+\cos x)^{2}}}}
=
sin
x
1
+
cos
x
.
{\displaystyle ={\sin x \over 1+\cos x}.}
Tương tự, lại nhân với mẫu số và tử số của phương trình (1) bởi 1 − cos x , rồi đơn giản hóa:
tan
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
−
cos
x
)
=
±
(
1
−
cos
x
)
2
(
1
−
cos
2
x
)
{\displaystyle \tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1-\cos x) \over (1+\cos x)(1-\cos x)}}=\pm \,{\sqrt {(1-\cos x)^{2} \over (1-\cos ^{2}x)}}}
=
1
−
cos
x
sin
x
.
{\displaystyle ={1-\cos x \over \sin x}.}
Suy ra:
tan
(
x
2
)
=
sin
(
x
)
1
+
cos
(
x
)
=
1
−
cos
(
x
)
sin
(
x
)
.
{\displaystyle \tan \left({\frac {x}{2}}\right)={\frac {\sin(x)}{1+\cos(x)}}={\frac {1-\cos(x)}{\sin(x)}}.}
Nếu
t
=
tan
(
x
2
)
,
{\displaystyle t=\tan \left({\frac {x}{2}}\right),}
thì:
sin
(
x
)
=
2
t
1
+
t
2
{\displaystyle \sin(x)={\frac {2t}{1+t^{2}}}}
and
cos
(
x
)
=
1
−
t
2
1
+
t
2
{\displaystyle \cos(x)={\frac {1-t^{2}}{1+t^{2}}}}
and
e
i
x
=
1
+
i
t
1
−
i
t
.
{\displaystyle e^{ix}={\frac {1+it}{1-it}}.}
sin
(
x
+
y
)
=
sin
x
cos
y
+
cos
x
sin
y
{\displaystyle \sin \left(x+y\right)=\sin x\cos y+\cos x\sin y}
cos
(
x
+
y
)
=
cos
x
cos
y
−
sin
x
sin
y
{\displaystyle \cos \left(x+y\right)=\cos x\cos y-\sin x\sin y}
sin
x
+
sin
y
=
2
sin
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \sin x+\sin y=2\sin \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)}
cos
x
+
cos
y
=
2
cos
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \cos x+\cos y=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)}
tan
x
+
tan
y
=
sin
(
x
+
y
)
cos
x
cos
y
{\displaystyle \tan x+\tan y={\frac {\sin \left(x+y\right)}{\cos x\cos y}}}
cot
x
+
cot
y
=
sin
(
x
+
y
)
sin
x
sin
y
{\displaystyle \cot x+\cot y={\frac {\sin \left(x+y\right)}{\sin x\sin y}}}
sin
(
x
−
y
)
=
sin
x
cos
y
−
cos
x
sin
y
{\displaystyle \sin \left(x-y\right)=\sin x\cos y-\cos x\sin y}
cos
(
x
−
y
)
=
cos
x
cos
y
+
sin
x
sin
y
{\displaystyle \cos \left(x-y\right)=\cos x\cos y+\sin x\sin y}
sin
x
−
sin
y
=
2
cos
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \sin x-\sin y=2\cos \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)}
cos
x
−
cos
y
=
−
2
sin
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \cos x-\cos y=-2\sin \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)}
tan
x
−
tan
y
=
sin
(
x
−
y
)
cos
x
cos
y
{\displaystyle \tan x-\tan y={\frac {\sin \left(x-y\right)}{\cos x\cos y}}}
cot
x
−
cot
y
=
−
sin
(
x
−
y
)
sin
x
sin
y
{\displaystyle \cot x-\cot y={\frac {-\sin \left(x-y\right)}{\sin x\sin y}}}
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
2
{\displaystyle \cos \left(x\right)\cos \left(y\right)={\cos \left(x+y\right)+\cos \left(x-y\right) \over 2}\;}
sin
(
x
)
sin
(
y
)
=
cos
(
x
−
y
)
−
cos
(
x
+
y
)
2
{\displaystyle \sin \left(x\right)\sin \left(y\right)={\cos \left(x-y\right)-\cos \left(x+y\right) \over 2}\;}
sin
(
x
)
cos
(
y
)
=
sin
(
x
−
y
)
+
sin
(
x
+
y
)
2
{\displaystyle \sin \left(x\right)\cos \left(y\right)={\sin \left(x-y\right)+\sin \left(x+y\right) \over 2}\;}
cos
2
(
x
)
=
1
+
cos
(
2
x
)
2
{\displaystyle \cos ^{2}(x)={1+\cos(2x) \over 2}}
sin
2
(
x
)
=
1
−
cos
(
2
x
)
2
{\displaystyle \sin ^{2}(x)={1-\cos(2x) \over 2}}
sin
2
(
x
)
cos
2
2
(
x
)
=
1
−
cos
(
4
x
)
4
{\displaystyle \sin ^{2}(x)\cos ^{2}2(x)={1-\cos(4x) \over 4}}
sin
3
(
x
)
=
2
sin
2
(
x
)
−
sin
(
3
x
)
4
{\displaystyle \sin ^{3}(x)={\frac {2\sin 2(x)-\sin(3x)}{4}}}
cos
3
(
x
)
=
3
cos
(
x
)
+
cos
(
3
x
)
4
{\displaystyle \cos ^{3}(x)={\frac {3\cos(x)+\cos(3x)}{4}}}
[ sửa ] [ sửa ] Hàm số lượng đường thẳng nghiêng
Z
=
z
∠
θ
=
X
2
+
Y
2
∠
t
a
n
−
1
Y
X
{\displaystyle Z=z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle tan^{-1}{\frac {Y}{X}}}
Hàm số lượng đường thẳng dọc
Y
=
y
∠
90
{\displaystyle Y=y\angle 90}
Hàm số lượng đường thẳng ngang
X
=
x
∠
0
{\displaystyle X=x\angle 0}
[ sửa ] Hàm số lượng đường tròn Z đơn vị
R
=
θ
{\displaystyle R=\theta }
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
Hàm số lượng đường tròn 1 đơn vị
1
=
(
X
Z
)
2
+
(
Y
Z
)
2
=
c
o
s
2
x
+
s
i
n
2
x
=
s
e
c
2
x
−
t
a
n
2
x
=
c
s
c
2
x
−
c
o
t
2
x
{\displaystyle 1=({\frac {X}{Z}})^{2}+({\frac {Y}{Z}})^{2}=cos^{2}x+sin^{2}x=sec^{2}x-tan^{2}x=csc^{2}x-cot^{2}x}

















































































































![{\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83064172516d2185efbd65172ed7cc9d3e701284)

![{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ddb7d13541806e35a6053ba614df98a87b655)








































![{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c5b6f1d86ff3f156fd65ff5857f5e95f89c10e)
![{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2a5db1feeaf9814ba2e7c2618c255f45f299a8)
![{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63777c0be192f9fe36871fbf7d21970aaed89899)
![{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c376b47de6ed1cfc662cad50bbc979688886f30)
![{\displaystyle 2S=[2a+(n-1)d]n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f47f5f57718103fa0610bc7149959105b3a09039)
![{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/220eac7734e9963f251e2cac7519edcaf6af5420)






























































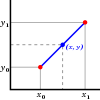















































![{\displaystyle s=\Delta xy+\Delta x{\frac {\Delta y}{2}}=\Delta x[y+{\frac {\Delta y}{2}}]=\Delta x[f(x)+{\frac {\Delta f(x)}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c1e8dd2152f12fb2ce22cb9e0aa68d4796d786)
![{\displaystyle s=\Delta x[f(x)+{\frac {\Delta f(x)}{2}}]={\frac {\Delta x}{2}}[2f(x)+f(x+\Delta x)-f(x)]={\frac {\Delta x}{2}}[f(x)+f(x+\Delta x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26da47a72c8fdda1d4c93ae221c06fe1ee8d89a5)





































































































![{\displaystyle [{\vec {a}},{\vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/008d8868e90625dc41200b2396382596923b8d9c)



![{\displaystyle [{\vec {n_{1}}},{\vec {n_{2}}}]=({\begin{vmatrix}B_{1}&C_{1}\\B_{2}&C_{2}\end{vmatrix}},{\begin{vmatrix}C_{1}&A_{1}\\C_{2}&A_{2}\end{vmatrix}},{\begin{vmatrix}A_{1}&B_{1}\\A_{2}&B_{2}\end{vmatrix}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cf919fe1c939d7c84b9d19d5bc78bd08474340)