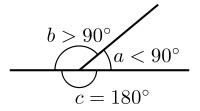Khi hai đường thẳng cắt nhau tại một điểm sẽ tạo ra một góc giữa hai đường thẳng . Góc có ký hiệu
∠
{\displaystyle \angle }
∠
A
{\displaystyle \angle A}
Góc đo bằng đơn vị Độ o hay Radian Rad
1
r
a
d
=
180
o
π
{\displaystyle 1rad={\frac {180^{o}}{\pi }}}
1
o
=
π
180
o
{\displaystyle 1^{o}={\frac {\pi }{180^{o}}}}
Thí dụ : Góc A bằng 30o
∠
A
=
30
0
=
π
6
r
a
d
{\displaystyle \angle A=30^{0}={\frac {\pi }{6}}rad}
Bảng liệt kê các loại góc
Thể loại góc Hình Định nghỉa
Góc nhọn
Góc nhọn là góc nhỏ hơn 90°
Góc vuông
Góc vuông là góc bằng 90° (1/4 vòng tròn);
Góc tù
Góc tù là góc lớn hơn 90° nhưng nhỏ hơn 180°
Góc bẹt
Góc bẹt là góc 180° (1/2 vòng tròn).
Góc phản
Góc phản là góc lớn hơn 180° nhưng nhỏ hơn 360°
Góc đầy
Góc đầy là góc bằng 360° (toàn bộ vòng tròn).
[ sửa ] 6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông
Hàm số lượng giác cơ bản
cos
x
{\displaystyle \cos x}
sin
x
{\displaystyle \sin x}
tan
x
{\displaystyle \tan x}
cot
x
{\displaystyle \cot x}
sec
x
{\displaystyle \sec x}
csc
x
{\displaystyle \csc x}
Tam giác vuông
b
c
{\displaystyle {\frac {b}{c}}}
a
c
{\displaystyle {\frac {a}{c}}}
a
b
{\displaystyle {\frac {a}{b}}}
b
a
{\displaystyle {\frac {b}{a}}}
1
b
{\displaystyle {\frac {1}{b}}}
1
a
{\displaystyle {\frac {1}{a}}}
[ sửa ] Các đẳng thức sau có thể dễ thấy trên vòng tròn đơn vị:
Tuần hoàn Đối xứng Tịnh tiến
sin
(
x
)
=
sin
(
x
+
2
k
π
)
{\displaystyle \sin(x)=\sin(x+2k\pi )\,}
sin
(
−
x
)
=
−
sin
(
x
)
{\displaystyle \sin(-x)=-\sin(x)\,}
sin
(
x
)
=
cos
(
π
2
−
x
)
{\displaystyle \sin(x)=\cos \left({\frac {\pi }{2}}-x\right)}
cos
(
x
)
=
cos
(
x
+
2
k
π
)
{\displaystyle \cos(x)=\cos(x+2k\pi )\,}
cos
(
−
x
)
=
cos
(
x
)
{\displaystyle \cos(-x)=\;\cos(x)\,}
cos
(
x
)
=
sin
(
π
2
−
x
)
{\displaystyle \cos(x)=\sin \left({\frac {\pi }{2}}-x\right)}
tan
(
x
)
=
tan
(
x
+
k
π
)
{\displaystyle \tan(x)=\tan(x+k\pi )\,}
tan
(
−
x
)
=
−
tan
(
x
)
{\displaystyle \tan(-x)=-\tan(x)\,}
tan
(
x
)
=
cot
(
π
2
−
x
)
{\displaystyle \tan(x)=\cot \left({\frac {\pi }{2}}-x\right)}
cot
(
−
x
)
=
−
cot
(
x
)
{\displaystyle \cot(-x)=-\cot(x)\,}
Đẳng thức sau cũng đôi khi hữu ích:
a
sin
x
+
b
cos
x
=
a
2
+
b
2
⋅
sin
(
x
+
φ
)
{\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )}
với
φ
=
{
a
r
c
t
a
n
(
b
/
a
)
,
n
e
^
´
u
a
≥
0
;
π
+
a
r
c
t
a
n
(
b
/
a
)
,
n
e
^
´
u
a
<
0.
{\displaystyle \varphi =\left\{{\begin{matrix}{\rm {arctan}}(b/a),&&{\mbox{n}}{\acute {\hat {\mbox{e}}}}{\mbox{u}}\ a\geq 0;\;\\\pi +{\rm {arctan}}(b/a),&&{\mbox{n}}{\acute {\hat {\mbox{e}}}}{\mbox{u}}\ a<0.\;\end{matrix}}\right.\;}
Các công thức sau có thể suy ra từ các công thức trên. Cũng có thể dùng công thức de Moivre với n = 2.
sin
(
2
x
)
=
2
sin
(
x
)
cos
(
x
)
{\displaystyle \sin(2x)=2\sin(x)\cos(x)\,}
cos
(
2
x
)
=
cos
2
(
x
)
−
sin
2
(
x
)
=
2
cos
2
(
x
)
−
1
=
1
−
2
sin
2
(
x
)
{\displaystyle \cos(2x)=\cos ^{2}(x)-\sin ^{2}(x)=2\cos ^{2}(x)-1=1-2\sin ^{2}(x)\,}
tan
(
2
x
)
=
2
tan
(
x
)
1
−
tan
2
(
x
)
{\displaystyle \tan(2x)={\frac {2\tan(x)}{1-\tan ^{2}(x)}}}
Công thức gíc kép có thể dùng để tìm bộ ba Pytago. Nếu (a, b, c) là bộ ba Pytago thì (a2 − b2, 2ab, c2) cũng vậy.
Ví dụ của trường hợp n = 3:
sin
(
3
x
)
=
3
sin
(
x
)
−
4
sin
3
(
x
)
{\displaystyle \sin(3x)=3\sin(x)-4\sin ^{3}(x)}
cos
(
3
x
)
=
4
cos
3
(
x
)
−
3
cos
(
x
)
{\displaystyle \cos(3x)=4\cos ^{3}(x)-3\cos(x)}
Nếu Tn là đa thức Chebyshev bậc n thì
cos
(
n
x
)
=
T
n
(
cos
(
x
)
)
.
{\displaystyle \cos(nx)=T_{n}(\cos(x)).\,}
công thức de Moivre:
cos
(
n
x
)
+
i
sin
(
n
x
)
=
(
cos
(
x
)
+
i
sin
(
x
)
)
n
{\displaystyle \cos(nx)+i\sin(nx)=(\cos(x)+i\sin(x))^{n}\,}
Hàm hạt nhân Dirichlet Dn(x) sẽ xuất hiện trong các công thức sau:
1
+
2
cos
(
x
)
+
2
cos
(
2
x
)
+
2
cos
(
3
x
)
+
⋯
+
2
cos
(
n
x
)
{\displaystyle 1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)\;}
=
sin
(
(
n
+
1
2
)
x
)
sin
(
x
/
2
)
{\displaystyle ={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}\;}
Hay theo công thức hồi quy:
sin
(
n
x
)
=
2
sin
(
(
n
−
1
)
x
)
cos
(
x
)
−
sin
(
(
n
−
2
)
x
)
{\displaystyle \sin(nx)=2\sin((n-1)x)\cos(x)-\sin((n-2)x)}
cos
(
n
x
)
=
2
cos
(
(
n
−
1
)
x
)
cos
(
x
)
−
cos
(
(
n
−
2
)
x
)
{\displaystyle \cos(nx)=2\cos((n-1)x)\cos(x)-\cos((n-2)x)}
[ sửa ]
cos
(
x
2
)
=
±
1
+
cos
(
x
)
2
{\displaystyle \cos \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(x)}{2}}}}
sin
(
x
2
)
=
±
1
−
cos
(
x
)
2
{\displaystyle \sin \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(x)}{2}}}}
tan
(
x
2
)
=
sin
(
x
/
2
)
cos
(
x
/
2
)
=
±
1
−
cos
x
1
+
cos
x
.
{\displaystyle \tan \left({\frac {x}{2}}\right)={\sin(x/2) \over \cos(x/2)}=\pm \,{\sqrt {1-\cos x \over 1+\cos x}}.\qquad \qquad }
x , rồi dùng định lý Pytago để đơn giản hóa:
tan
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
=
±
1
−
cos
2
x
(
1
+
cos
x
)
2
{\displaystyle \tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1+\cos x) \over (1+\cos x)(1+\cos x)}}=\pm \,{\sqrt {1-\cos ^{2}x \over (1+\cos x)^{2}}}}
=
sin
x
1
+
cos
x
.
{\displaystyle ={\sin x \over 1+\cos x}.}
Tương tự, lại nhân với mẫu số và tử số của phương trình (1) bởi 1 − cos x , rồi đơn giản hóa:
tan
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
−
cos
x
)
=
±
(
1
−
cos
x
)
2
(
1
−
cos
2
x
)
{\displaystyle \tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1-\cos x) \over (1+\cos x)(1-\cos x)}}=\pm \,{\sqrt {(1-\cos x)^{2} \over (1-\cos ^{2}x)}}}
=
1
−
cos
x
sin
x
.
{\displaystyle ={1-\cos x \over \sin x}.}
Suy ra:
tan
(
x
2
)
=
sin
(
x
)
1
+
cos
(
x
)
=
1
−
cos
(
x
)
sin
(
x
)
.
{\displaystyle \tan \left({\frac {x}{2}}\right)={\frac {\sin(x)}{1+\cos(x)}}={\frac {1-\cos(x)}{\sin(x)}}.}
Nếu
t
=
tan
(
x
2
)
,
{\displaystyle t=\tan \left({\frac {x}{2}}\right),}
thì:
sin
(
x
)
=
2
t
1
+
t
2
{\displaystyle \sin(x)={\frac {2t}{1+t^{2}}}}
and
cos
(
x
)
=
1
−
t
2
1
+
t
2
{\displaystyle \cos(x)={\frac {1-t^{2}}{1+t^{2}}}}
and
e
i
x
=
1
+
i
t
1
−
i
t
.
{\displaystyle e^{ix}={\frac {1+it}{1-it}}.}
[ sửa ]
sin
(
x
+
y
)
=
sin
x
cos
y
+
cos
x
sin
y
{\displaystyle \sin \left(x+y\right)=\sin x\cos y+\cos x\sin y}
cos
(
x
+
y
)
=
cos
x
cos
y
−
sin
x
sin
y
{\displaystyle \cos \left(x+y\right)=\cos x\cos y-\sin x\sin y}
sin
x
+
sin
y
=
2
sin
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \sin x+\sin y=2\sin \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)}
cos
x
+
cos
y
=
2
cos
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \cos x+\cos y=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)}
tan
x
+
tan
y
=
sin
(
x
+
y
)
cos
x
cos
y
{\displaystyle \tan x+\tan y={\frac {\sin \left(x+y\right)}{\cos x\cos y}}}
cot
x
+
cot
y
=
sin
(
x
+
y
)
sin
x
sin
y
{\displaystyle \cot x+\cot y={\frac {\sin \left(x+y\right)}{\sin x\sin y}}}
[ sửa ]
sin
(
x
−
y
)
=
sin
x
cos
y
−
cos
x
sin
y
{\displaystyle \sin \left(x-y\right)=\sin x\cos y-\cos x\sin y}
cos
(
x
−
y
)
=
cos
x
cos
y
+
sin
x
sin
y
{\displaystyle \cos \left(x-y\right)=\cos x\cos y+\sin x\sin y}
sin
x
−
sin
y
=
2
cos
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \sin x-\sin y=2\cos \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)}
cos
x
−
cos
y
=
−
2
sin
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \cos x-\cos y=-2\sin \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)}
tan
x
−
tan
y
=
sin
(
x
−
y
)
cos
x
cos
y
{\displaystyle \tan x-\tan y={\frac {\sin \left(x-y\right)}{\cos x\cos y}}}
cot
x
−
cot
y
=
−
sin
(
x
−
y
)
sin
x
sin
y
{\displaystyle \cot x-\cot y={\frac {-\sin \left(x-y\right)}{\sin x\sin y}}}
[ sửa ]
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
2
{\displaystyle \cos \left(x\right)\cos \left(y\right)={\cos \left(x+y\right)+\cos \left(x-y\right) \over 2}\;}
sin
(
x
)
sin
(
y
)
=
cos
(
x
−
y
)
−
cos
(
x
+
y
)
2
{\displaystyle \sin \left(x\right)\sin \left(y\right)={\cos \left(x-y\right)-\cos \left(x+y\right) \over 2}\;}
sin
(
x
)
cos
(
y
)
=
sin
(
x
−
y
)
+
sin
(
x
+
y
)
2
{\displaystyle \sin \left(x\right)\cos \left(y\right)={\sin \left(x-y\right)+\sin \left(x+y\right) \over 2}\;}
[ sửa ]
cos
2
(
x
)
=
1
+
cos
(
2
x
)
2
{\displaystyle \cos ^{2}(x)={1+\cos(2x) \over 2}}
sin
2
(
x
)
=
1
−
cos
(
2
x
)
2
{\displaystyle \sin ^{2}(x)={1-\cos(2x) \over 2}}
sin
2
(
x
)
cos
2
2
(
x
)
=
1
−
cos
(
4
x
)
4
{\displaystyle \sin ^{2}(x)\cos ^{2}2(x)={1-\cos(4x) \over 4}}
sin
3
(
x
)
=
2
sin
2
(
x
)
−
sin
(
3
x
)
4
{\displaystyle \sin ^{3}(x)={\frac {2\sin 2(x)-\sin(3x)}{4}}}
cos
3
(
x
)
=
3
cos
(
x
)
+
cos
(
3
x
)
4
{\displaystyle \cos ^{3}(x)={\frac {3\cos(x)+\cos(3x)}{4}}}
[ sửa ] 6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông
Hàm số lượng giác cơ bản
cos
−
1
x
{\displaystyle \cos ^{-1}x}
sin
−
1
x
{\displaystyle \sin ^{-1}x}
tan
−
1
x
{\displaystyle \tan ^{-1}x}
cot
−
1
x
{\displaystyle \cot ^{-1}x}
sec
−
1
x
{\displaystyle \sec ^{-1}x}
csc
−
1
x
{\displaystyle \csc ^{-1}x}
Tam giác vuông
b
c
{\displaystyle {\frac {b}{c}}}
a
c
{\displaystyle {\frac {a}{c}}}
a
b
{\displaystyle {\frac {a}{b}}}
b
a
{\displaystyle {\frac {b}{a}}}
1
b
{\displaystyle {\frac {1}{b}}}
1
a
{\displaystyle {\frac {1}{a}}}
Các hàm lượng giác nghịch đảo cũng có thể được định nghĩa bằng chuỗi vô hạn:
arcsin
z
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
2
n
+
1
(
2
n
+
1
)
|
z
|
<
1
{\displaystyle {\begin{matrix}\arcsin z&=&z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|<1}
arccos
z
=
π
2
−
arcsin
z
=
π
2
−
(
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
2
n
+
1
(
2
n
+
1
)
|
z
|
<
1
{\displaystyle {\begin{matrix}\arccos z&=&{\frac {\pi }{2}}-\arcsin z\\&=&{\frac {\pi }{2}}-(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|<1}
arctan
z
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
|
z
|
<
1
{\displaystyle {\begin{matrix}\arctan z&=&z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\end{matrix}}\,\quad \left|z\right|<1}
arccsc
z
=
arcsin
(
z
−
1
)
=
z
−
1
+
(
1
2
)
z
−
3
3
+
(
1
⋅
3
2
⋅
4
)
z
−
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
−
7
7
+
⋯
=
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
−
(
2
n
+
1
)
2
n
+
1
|
z
|
>
1
{\displaystyle {\begin{matrix}\operatorname {arccsc} z&=&\arcsin \left(z^{-1}\right)\\&=&z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{2n+1}}\end{matrix}}\,\quad \left|z\right|>1}
arcsec
z
=
arccos
(
z
−
1
)
=
π
2
−
(
z
−
1
+
(
1
2
)
z
−
3
3
+
(
1
⋅
3
2
⋅
4
)
z
−
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
−
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
−
(
2
n
+
1
)
(
2
n
+
1
)
|
z
|
>
1
{\displaystyle {\begin{matrix}\operatorname {arcsec} z&=&\arccos \left(z^{-1}\right)\\&=&{\frac {\pi }{2}}-(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|>1}
arccot
z
=
π
2
−
arctan
z
=
π
2
−
(
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
|
z
|
<
1
{\displaystyle {\begin{matrix}\operatorname {arccot} z&=&{\frac {\pi }{2}}-\arctan z\\&=&{\frac {\pi }{2}}-(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\end{matrix}}\,\quad \left|z\right|<1}
Chúng cũng có thể được định nghĩa thông qua các biểu thức sau, dựa vào tính chất chúng là đạo hàm của các hàm khác.
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
<
1
{\displaystyle \arcsin \left(x\right)=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1}
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
<
1
{\displaystyle \arccos \left(x\right)=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1}
arctan
(
x
)
=
∫
0
x
1
1
+
z
2
d
z
,
∀
x
∈
R
{\displaystyle \arctan \left(x\right)=\int _{0}^{x}{\frac {1}{1+z^{2}}}\,\mathrm {d} z,\quad \forall x\in \mathbb {R} }
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
z
>
0
{\displaystyle \operatorname {arccot} \left(x\right)=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,\mathrm {d} z,\quad z>0}
arcsec
(
x
)
=
∫
x
1
1
|
z
|
z
2
−
1
d
z
,
x
>
1
{\displaystyle \operatorname {arcsec} \left(x\right)=\int _{x}^{1}{\frac {1}{|z|{\sqrt {z^{2}-1}}}}\,\mathrm {d} z,\quad x>1}
arccsc
(
x
)
=
∫
x
∞
−
1
|
z
|
z
2
−
1
d
z
,
x
>
1
{\displaystyle \operatorname {arccsc} \left(x\right)=\int _{x}^{\infty }{\frac {-1}{|z|{\sqrt {z^{2}-1}}}}\,\mathrm {d} z,\quad x>1}
Công thức trên cho phép mở rộng hàm lượng giác nghịch đảo ra cho các biến số phức|phức:
arcsin
(
z
)
=
−
i
log
(
i
(
z
+
1
−
z
2
)
)
{\displaystyle \arcsin(z)=-i\log \left(i\left(z+{\sqrt {1-z^{2}}}\right)\right)}
arccos
(
z
)
=
−
i
log
(
z
+
z
2
−
1
)
{\displaystyle \arccos(z)=-i\log \left(z+{\sqrt {z^{2}-1}}\right)}
arctan
(
z
)
=
i
2
log
(
1
−
i
z
1
+
i
z
)
{\displaystyle \arctan(z)={\frac {i}{2}}\log \left({\frac {1-iz}{1+iz}}\right)}
Các định lý định nghỉa tương quan giửa các cạnh và góc trong tam giác
Định lý Hình Ý nghỉa Công thức
Định lý Cosine
định lý cos biểu diễn sự liên quan giữa chiều dài của các cạnh của một tam giác phẳng với cosin của góc
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,}
b
2
=
a
2
+
c
2
−
2
a
c
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta \,}
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}
Định lý Sine
định lý sin (hay định luật sin , công thức sin ) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng.
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}\!}
sin
A
a
=
sin
B
b
=
sin
C
c
.
{\displaystyle {\frac {\sin A}{a}}\,=\,{\frac {\sin B}{b}}\,=\,{\frac {\sin C}{c}}.\!}
Định lý Pytago
Định lý cos khái quát định lý Pytago (định lý Pytago là trường hợp riêng trong tam giác vuông): nếu γ là góc vuông thì cos γ = 0, và định lý cos trở thành định lý Pytago
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}\,}
Tam giác vuông là một loại tam giác có 2 cạnh vuông góc với nhau cắt nhau tại một điểm tạo nên một góc vuông bằng
90
o
{\displaystyle 90^{o}}
3 điểm .
A
,
B
,
C
{\displaystyle A,B,C}
3 cạnh .
A
B
,
B
C
,
C
A
{\displaystyle AB,BC,CA}
A
C
¯
⊥
C
B
¯
{\displaystyle {\overline {AC}}\perp {\overline {CB}}}
3 góc .
∠
A
,
∠
B
,
∠
C
{\displaystyle \angle A,\angle B,\angle C}
∠
C
=
90
o
{\displaystyle \angle C=90^{o}}
Chu vi .
a
+
b
+
c
{\displaystyle a+b+c}
Diện tích .
1
2
a
b
{\displaystyle {\frac {1}{2}}ab}
Thể tích .
1
2
a
b
{\displaystyle {\frac {1}{2}}ab}
[ sửa ] Định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông
Hàm số lượng giác cơ bản
cos
x
{\displaystyle \cos x}
sin
x
{\displaystyle \sin x}
tan
x
{\displaystyle \tan x}
cot
x
{\displaystyle \cot x}
sec
x
{\displaystyle \sec x}
csc
x
{\displaystyle \csc x}
Tam giác vuông
b
c
{\displaystyle {\frac {b}{c}}}
a
c
{\displaystyle {\frac {a}{c}}}
a
b
{\displaystyle {\frac {a}{b}}}
b
a
{\displaystyle {\frac {b}{a}}}
1
b
{\displaystyle {\frac {1}{b}}}
1
a
{\displaystyle {\frac {1}{a}}}
Định nghỉa tương quan giửa 3 cạnh trong tam giác vuông
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}}
Trong lượng giác, đường thẳng nghiêng được xem như đường thẳng có một độ dài nghiêng ở một góc độ
Z
=
z
∠
θ
=
X
2
+
Y
2
∠
tan
−
1
Y
X
{\displaystyle Z=z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle \tan ^{-1}{\frac {Y}{X}}}
X
=
Z
cos
θ
=
x
−
x
o
{\displaystyle X=Z\cos \theta =x-x_{o}}
Y
=
Z
sin
θ
=
y
−
y
o
{\displaystyle Y=Z\sin \theta =y-y_{o}}
Z
=
X
2
+
Y
2
{\displaystyle Z={\sqrt {X^{2}+Y^{2}}}}
θ
=
tan
−
1
Y
X
{\displaystyle \theta =\tan ^{-1}{\frac {Y}{X}}}
Trong đại số qua bất kỳ 2 điểm
(
x
o
,
y
o
)
{\displaystyle (x_{o},y_{o})}
(
x
,
y
)
{\displaystyle (x,y)}
a
=
y
−
y
o
x
−
x
o
=
Δ
y
Δ
x
=
Y
X
{\displaystyle a={\frac {y-y_{o}}{x-x_{o}}}={\frac {\Delta y}{\Delta x}}={\frac {Y}{X}}}
y
−
y
o
=
a
(
x
−
x
o
)
{\displaystyle y-y_{o}=a(x-x_{o})}
Y
=
a
X
{\displaystyle Y=aX}
X
=
Y
a
{\displaystyle X={\frac {Y}{a}}}
[ sửa ] Phương trình đường thẳng có dạng tổng quát
a
x
+
b
=
0
{\displaystyle ax+b=0}
Giải phương trình
a
x
+
b
=
0
{\displaystyle ax+b=0}
x
+
b
a
=
0
{\displaystyle x+{\frac {b}{a}}=0}
Nghiệm số phương trình
x
=
−
b
a
{\displaystyle x=-{\frac {b}{a}}}
X
→
=
X
i
→
{\displaystyle {\vec {X}}=X{\vec {i}}}
Y
→
=
Y
j
→
{\displaystyle {\vec {Y}}=Y{\vec {j}}}
Z
→
=
Z
k
→
{\displaystyle {\vec {Z}}=Z{\vec {k}}}
Hay
A
→
=
A
a
→
{\displaystyle {\vec {A}}=A{\vec {a}}}
a
→
=
A
→
A
{\displaystyle {\vec {a}}={\frac {\vec {A}}{A}}}
A
=
A
→
a
{\displaystyle A={\frac {\vec {A}}{a}}}
R - Bán kính vòng tròn
D - Đường kính vòng tròn
P
=
d
π
=
2
r
π
{\displaystyle P=d\pi =2r\pi }
S
=
r
2
.
π
{\displaystyle S=r^{2}.\pi }
A
=
(
d
2
.
π
)
/
4
{\displaystyle A=(d^{2}.\pi )/4}
Z
=
X
2
+
Y
2
{\displaystyle Z={\sqrt {X^{2}+Y^{2}}}}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
Z
Z
2
=
X
Z
2
+
Y
Z
2
{\displaystyle {\frac {Z}{Z}}^{2}={\frac {X}{Z}}^{2}+{\frac {Y}{Z}}^{2}}
1
=
cos
2
x
+
s
i
n
2
x
{\displaystyle 1=\cos ^{2}x+sin^{2}x}
1
=
tan
2
x
+
s
e
c
2
x
{\displaystyle 1=\tan ^{2}x+sec^{2}x}
1
=
cot
2
x
+
c
s
c
2
x
{\displaystyle 1=\cot ^{2}x+csc^{2}x}
[ sửa ]
Z
2
=
X
2
+
Y
2
=
0
{\displaystyle Z^{2}=X^{2}+Y^{2}=0}
X
=
−
Y
2
=
±
j
Y
{\displaystyle X={\sqrt {-Y^{2}}}=\pm jY}
Y
=
−
X
2
=
±
j
X
{\displaystyle Y={\sqrt {-X^{2}}}=\pm jX}
R
→
=
X
→
+
Y
→
=
X
i
→
+
Y
j
→
{\displaystyle {\vec {R}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}}
R
→
=
R
r
→
{\displaystyle {\vec {R}}=R{\vec {r}}}
s
=
r
θ
{\displaystyle s=r\theta }
θ
=
s
r
{\displaystyle \theta ={\frac {s}{r}}}