Tủ sách/Sách công thức/Sách công thức Toán

Trang này được đề nghị xóa nhanh với lý do: Spam of Quách trung thành 205.189.94.88, copied from Sách công thức Nếu bạn không đồng ý xóa bài, hãy thêm bản mẫu {{chờ chút}} dưới bản mẫu này này và nhanh chóng nêu lý do tại trang thảo luận. Nếu bài bị đề nghị xóa vì nội dung có chất lượng thấp, mời bạn giúp cải thiện nó. Sửa đổi cuối: 2001:EE0:1A4E:4E6C:3C50:BD68:E9F1:A677 (thảo luận | đóng góp) vào 64 phút trước. (làm mới)

Đại số

Phép toán Số nguyên

Số nguyên   $I={I<0,I=0,I>0}$

Toán Số nguyên	Công thức
Cộng trừ nhân chia số nguyên với số không	$a+0=a$ $a-0=a$ $a\times 0=0$ $a/0=oo$
Cộng trừ nhân chia số nguyên dương với số nguyên âm	$a+(-a)=0$ $a-(-a)=2a$ $a\times (-a)=-a^{2}$ $a/(-a)=-1$
Cộng trừ nhân chia số nguyên dương với số nguyên dương	$a+a=2a$ $a-a=0$ $a\times a=a^{2}$ ${\frac {a}{a}}=1$
Lũy thừa số nguyên	$a^{0}=1$ $a^{n}=a\times a\times a...\times a$ $(-a)^{n}=a^{n}$ . $n=2m$$(-a)^{n}=-a^{n}$ . Với $n=2m+1$
Căn số nguyên	${\sqrt {0}}=0$ ${\sqrt {1}}=1$ ${\sqrt {(-1)}}=j$

Phép toán Lũy thừa

$a^{n}=a\times a\times a\times a...\times a$

Toán lủy thừa	Công thức
Lủy thừa không	$a^{0}=1$
Lủy thừa 1	$a^{1}=a$
Lủy thừa của số không	$0^{n}$
Lủy thừa của số 1	$1^{n}=1$
Lủy thừa trừ	$a^{-n}={\frac {1}{a^{n}}}$
Lủy thừa phân số	$a^{\frac {m}{n}}=n{\sqrt {a^{m}}}$
Lủy thừa của số nguyên âm	$(-a)^{n}=a^{n}$ Với $n=2m$. $(-a)^{n}=-a^{n}$ . Với $n=2m+1$
Lủy thừa của số nguyên dương	$(+a)^{n}=a^{n}$
Lủy thừa của lủy thừa	$(a^{m})^{n}=(a^{n})^{m}=a^{mn}$
Lủy thừa của tích hai số	$(ab)^{m}=a^{m}\times b^{m}$
Lủy thừa của thương hai số	$({\frac {a}{b}})^{m}={\frac {a^{m}}{a^{n}}}$
Lủy thừa của căn	$({\sqrt {a^{n}}})^{m}=a^{\frac {m}{n}}$
Cộng trừ nhân chia 2 lủy thừa	$a^{m}+a^{n}=a^{m}(1+a^{n-m})$ $a^{m}-a^{n}=a^{m}(1-a^{n-m})$ $a^{m}\times a^{n}=a^{m+n}$ $a^{m}/a^{n}=a^{m-n}$
Lủy thừa của tổng hai số	$(a+b)^{n}=\underbrace {(a+b)\times (a+b)\cdots \times (a+b)} _{n}$ $(a+b)^{n}=a^{n}+C_{n-1}a^{n-1}b+...+C_{1}ab^{n-1}+b^{n}$ $(a+b)^{0}=1$ $(a+b)^{1}=a+b$ $(a+b)^{2}=(a+b)\times (a+b)=a^{2}+2ab+b^{2}$ $(a+b)^{3}=(a+b)\times (a+b)\times (a+b)=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
Lủy thừa của hiệu hai số	$(a-b)^{n}=\underbrace {(a-b)\times (a-b)\cdots \times (a-b)} _{n}$ $(a-b)^{0}=1$ $(a-b)^{1}=a+b$ $(a-b)^{2}=(a-b)\times (a-b)=a^{2}-2ab+b^{2}$ $(a-b)^{3}=(a-b)\times (a-b)\times (a-b)=a^{3}-3a^{2}b+3ab^{2}-b^{3}$
Hiệu 2 lũy thừa	$a^{2}-b^{2}=(a+b)\times (a-b)$
Tổng 2 lũy thừa	$a^{2}+b^{2}=(a+b)^{2}-2ab=(a-b)^{2}+2ab$

Phép toán Toán căn

${\sqrt[{n}]{a}}=b$ khi có $a=b^{n}$

Toán căn số	Công thức
Căn và lủy thừa	$n{\sqrt {a}}=a^{\frac {1}{n}}$
Căn của số nguyên	${\sqrt {0}}=Error$ ${\sqrt {1}}=1$ ${\sqrt {-1}}=j$
Căn lủy thừa	${\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}$
Căn thương số	${\sqrt {\frac {a}{b}}}={\frac {\sqrt {a}}{\sqrt {b}}}$ ${\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}$
Căn tích số	${\sqrt {ab}}$ = ${\sqrt {a}}$ ${\sqrt {b}}$
Vô căn	$a{\sqrt {a}}={\sqrt {a^{2}\times a}}={\sqrt {a^{3}}}$
Ra căn	${\sqrt {a^{n}}}=a{\sqrt {a^{n-2}}}$

Phép toán Toán log

$Log_{a}b=c$ khi có $a^{c}=b$

Toán Log	Công thức
Viết tắc	$Log=Log_{10}$ $Ln=Log_{2}$
Log 1	$Log(1)=0$
Log lũy thừa	$Log_{n}(A)^{n}=A$
Lũy thừa log	$B^{Log_{B}(A)}=A$
Log của tích số	$Log(AB)=LogA+LogB$
Log của thương số	$Log({\frac {A}{B}})=LogA-LogB$
Log của lủy thừa	$Log(A^{n})=nLogA$
Đổi nền log	$Log_{a}x={\frac {Logx}{Loga}}$

Phép toán Toán số phức

Số phức được biểu diển như ở dưới đây

Số phức	Thuận $Z$	Nghịch $Z^{*}$
Biểu diển dưới dạng xy	$Z=x+jy$	$Z=x-jy$
Biểu diển dưới dạng Zθ	$Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle tan^{-1}{\frac {y}{x}}$	$Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle -tan^{-1}{\frac {y}{x}}$
Biểu diển dưới dạng hàm số lượng giác	$Z=z(cos\theta +jsin\theta )$	$Z=z(cos\theta -jsin\theta )$
Biểu diển dưới lũy thừa của e	$Z=ze^{j\theta }$	$Z=ze^{-j\theta }$

Toán số phức được thực thi như sau

Toán Số phức	Toán cộng	Toán trừ	Toán nhân	Toán chia
$x+jy$ và $x-jy$	$2x$	$2y$	$x^{2}-y^{2}$	${\frac {x^{2}-y^{2}}{x-jy}}$
$x+jy$ và $x-jy$	$2x$	$2y$	$x^{2}-y^{2}$	${\frac {x^{2}-y^{2}}{x-jy}}$
$x+jy$ và $x-jy$	$2x$	$2y$	$x^{2}-y^{2}$	${\frac {x^{2}-y^{2}}{x-jy}}$
$Z=ze^{j\theta }$ và $Z=ze^{-j\theta }$	$z(e^{j\theta }+e^{-j\theta })$	$z(e^{j\theta }-e^{-j\theta })$	$z^{2}$	$e^{j2\theta }$

Định lý Demoive

$(Z\angle \theta )^{n}=Z^{n}\angle n\theta$

Hình học

Tam giác vuông Pythagore

Vector các cạnh

${\vec {X}}=X{\vec {i}}$ . Vector cạnh ngang

${\vec {Y}}=y{\vec {J}}$ . Vector cạnh dọc

${\vec {Z}}=Z{\vec {K}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}$ . Vector cạnh nghiêng

Tương quan góc và cạnh

$cos\theta ={\frac {X}{Z}}$

$sin\theta ={\frac {Y}{Z}}$

$sec\theta ={\frac {1}{X}}$

$csc\theta ={\frac {1}{Y}}$

$tan\theta ={\frac {Y}{X}}$

$cot\theta ={\frac {X}{Y}}$

Đường dài các cạnh

$X={\frac {Y}{Z}}=x-x_{o}=\Delta x$

$Y=ZX=x-x_{o}=y-y_{o}=\Delta y$

$Z={\frac {Y}{X}}={\frac {y-y_{o}}{x-x_{o}}}={\frac {\Delta y}{\Delta x}}={\sqrt {X^{2}+Y^{2}}}$

Góc độ nghiêng

$\theta =tan^{-1}Z=tan^{-1}{\frac {Y}{Z}}$

Hàm số đương thẳng nghiêng

$Z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle tan^{-1}{\frac {Y}{X}}$

$Y=ZX$

$y=y_{o}+ZX$

Die^.n tích dưới hình

$S=X(y_{o}+{\frac {Y}{2}})=X(y_{o}+{\frac {ZX}{2}})=X(y-{\frac {ZX}{2}})$

$S=({\frac {y-y_{o}}{Z}})({\frac {2y_{o}+y-y_{o}}{2}})={\frac {y^{2}-y_{o}^{2}}{2Z}}$

Với

$Y=ZX$

$X={\frac {Y}{Z}}={\frac {y-y_{o}}{Z}}$

$y-y_{o}=ZX$

$y=y_{o}+ZX$

$y_{o}=y-ZX$

Lượng giác

Góc

Khi hai đường thẳng cắt nhau tại một điểm sẽ tạo ra một góc giữa hai đường thẳng . Góc có ký hiệu $\angle$ . Thí dụ 2 đường thẳng AB và AC cắt nhau tại một điểm a tạo ra góc A : $\angle A$

Góc đo bằng đơn vị Độ ^o hay Radian Rad

$1rad={\frac {180^{o}}{\pi }}$

$1^{o}={\frac {\pi }{180^{o}}}$

Thí dụ : Góc A bằng 30^o

$\angle A=30^{0}={\frac {\pi }{6}}rad$

Bảng liệt kê các loại góc

Thể loại góc	Hình	Định nghỉa
Góc nhọn		Góc nhọn là góc nhỏ hơn 90°
Góc vuông		Góc vuông là góc bằng 90° (1/4 vòng tròn);
Góc tù		Góc tù là góc lớn hơn 90° nhưng nhỏ hơn 180°
Góc bẹt		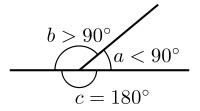Góc bẹt là góc 180° (1/2 vòng tròn).
Góc phản		Góc phản là góc lớn hơn 180° nhưng nhỏ hơn 360°
Góc đầy		Góc đầy là góc bằng 360° (toàn bộ vòng tròn).

Hàm số lượng giác

6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông

Hàm số lượng giác cơ bản	$\cos x$	$\sin x$	$\tan x$	$\cot x$	$\sec x$	$\csc x$
Tam giác vuông	${\frac {b}{c}}$	${\frac {a}{c}}$	${\frac {a}{b}}$	${\frac {b}{a}}$	${\frac {1}{b}}$	${\frac {1}{a}}$
Đồ thị

Tính chất Tuần hoàn, đối xứng và tịnh tiến

Các đẳng thức sau có thể dễ thấy trên vòng tròn đơn vị:

Tuần hoàn	Đối xứng	Tịnh tiến
$\sin(x)=\sin(x+2k\pi )\,$	$\sin(-x)=-\sin(x)\,$	$\sin(x)=\cos \left({\frac {\pi }{2}}-x\right)$
$\cos(x)=\cos(x+2k\pi )\,$	$\cos(-x)=\;\cos(x)\,$	$\cos(x)=\sin \left({\frac {\pi }{2}}-x\right)$
$\tan(x)=\tan(x+k\pi )\,$	$\tan(-x)=-\tan(x)\,$	$\tan(x)=\cot \left({\frac {\pi }{2}}-x\right)$
	$\cot(-x)=-\cot(x)\,$

Hàm số góc bội

• Bội hai

Các công thức sau có thể suy ra từ các công thức trên. Cũng có thể dùng công thức de Moivre với n = 2.

$\sin(2x)=2\sin(x)\cos(x)\,$

$\cos(2x)=\cos ^{2}(x)-\sin ^{2}(x)=2\cos ^{2}(x)-1=1-2\sin ^{2}(x)\,$

$\tan(2x)={\frac {2\tan(x)}{1-\tan ^{2}(x)}}$

Công thức gíc kép có thể dùng để tìm bộ ba Pytago. Nếu (a, b, c) là bộ ba Pytago thì (a2 − b2, 2ab, c2) cũng vậy.

• Bội ba

Ví dụ của trường hợp n = 3:

$\sin(3x)=3\sin(x)-4\sin ^{3}(x)$

$\cos(3x)=4\cos ^{3}(x)-3\cos(x)$

• Tổng quát

Nếu Tn là đa thức Chebyshev bậc n thì

$\cos(nx)=T_{n}(\cos(x)).\,$

công thức de Moivre:

$\cos(nx)+i\sin(nx)=(\cos(x)+i\sin(x))^{n}\,$

Hàm hạt nhân Dirichlet Dn(x) sẽ xuất hiện trong các công thức sau:

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)\;$

$={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}\;$

Hay theo công thức hồi quy:

$\sin(nx)=2\sin((n-1)x)\cos(x)-\sin((n-2)x)$

$\cos(nx)=2\cos((n-1)x)\cos(x)-\cos((n-2)x)$=

Hàm số góc chia đôi

$\cos \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(x)}{2}}}$

$\sin \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(x)}{2}}}$

$\tan \left({\frac {x}{2}}\right)={\sin(x/2) \over \cos(x/2)}=\pm \,{\sqrt {1-\cos x \over 1+\cos x}}.\qquad \qquad$

Từ trên , Nhân với mẫu số và tử số 1 + cos x, rồi dùng định lý Pytago để đơn giản hóa:

$\tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1+\cos x) \over (1+\cos x)(1+\cos x)}}=\pm \,{\sqrt {1-\cos ^{2}x \over (1+\cos x)^{2}}}$

$={\sin x \over 1+\cos x}.$

Tương tự, lại nhân với mẫu số và tử số của phương trình (1) bởi 1 − cos x, rồi đơn giản hóa:

$\tan \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1-\cos x) \over (1+\cos x)(1-\cos x)}}=\pm \,{\sqrt {(1-\cos x)^{2} \over (1-\cos ^{2}x)}}$

$={1-\cos x \over \sin x}.$

Suy ra:

$\tan \left({\frac {x}{2}}\right)={\frac {\sin(x)}{1+\cos(x)}}={\frac {1-\cos(x)}{\sin(x)}}.$

Nếu

$t=\tan \left({\frac {x}{2}}\right),$

thì:

$\sin(x)={\frac {2t}{1+t^{2}}}$

and

$\cos(x)={\frac {1-t^{2}}{1+t^{2}}}$

and

$e^{ix}={\frac {1+it}{1-it}}.$

Công thức tổng của 2 góc

$\sin \left(x+y\right)=\sin x\cos y+\cos x\sin y$

$\cos \left(x+y\right)=\cos x\cos y-\sin x\sin y$

$\sin x+\sin y=2\sin \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)$

$\cos x+\cos y=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)$

$\tan x+\tan y={\frac {\sin \left(x+y\right)}{\cos x\cos y}}$

$\cot x+\cot y={\frac {\sin \left(x+y\right)}{\sin x\sin y}}$

Công thức hiệu của 2 góc

$\sin \left(x-y\right)=\sin x\cos y-\cos x\sin y$

$\cos \left(x-y\right)=\cos x\cos y+\sin x\sin y$

$\sin x-\sin y=2\cos \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)$

$\cos x-\cos y=-2\sin \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)$

$\tan x-\tan y={\frac {\sin \left(x-y\right)}{\cos x\cos y}}$

$\cot x-\cot y={\frac {-\sin \left(x-y\right)}{\sin x\sin y}}$

Công thức tích 2 góc

$\cos \left(x\right)\cos \left(y\right)={\cos \left(x+y\right)+\cos \left(x-y\right) \over 2}\;$

$\sin \left(x\right)\sin \left(y\right)={\cos \left(x-y\right)-\cos \left(x+y\right) \over 2}\;$

$\sin \left(x\right)\cos \left(y\right)={\sin \left(x-y\right)+\sin \left(x+y\right) \over 2}\;$

Công thức lũy thừa của góc

$\cos ^{2}(x)={1+\cos(2x) \over 2}$

$\sin ^{2}(x)={1-\cos(2x) \over 2}$

$\sin ^{2}(x)\cos ^{2}2(x)={1-\cos(4x) \over 4}$

$\sin ^{3}(x)={\frac {2\sin 2(x)-\sin(3x)}{4}}$

$\cos ^{3}(x)={\frac {3\cos(x)+\cos(3x)}{4}}$

Hàm số lượng giác nghịch

Định nghỉa

6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông

Hàm số lượng giác cơ bản	$\cos ^{-1}x$	$\sin ^{-1}x$	$\tan ^{-1}x$	$\cot ^{-1}x$	$\sec ^{-1}x$	$\csc ^{-1}x$
Tam giác vuông	${\frac {b}{c}}$	${\frac {a}{c}}$	${\frac {a}{b}}$	${\frac {b}{a}}$	${\frac {1}{b}}$	${\frac {1}{a}}$
Đồ thị

Tính chất

Chuổi Số

Các hàm lượng giác nghịch đảo cũng có thể được định nghĩa bằng chuỗi vô hạn:

${\begin{matrix}\arcsin z&=&z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|<1$

${\begin{matrix}\arccos z&=&{\frac {\pi }{2}}-\arcsin z\\&=&{\frac {\pi }{2}}-(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|<1$

${\begin{matrix}\arctan z&=&z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\end{matrix}}\,\quad \left|z\right|<1$

${\begin{matrix}\operatorname {arccsc} z&=&\arcsin \left(z^{-1}\right)\\&=&z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&=&\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{2n+1}}\end{matrix}}\,\quad \left|z\right|>1$

${\begin{matrix}\operatorname {arcsec} z&=&\arccos \left(z^{-1}\right)\\&=&{\frac {\pi }{2}}-(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{(2n+1)}}\end{matrix}}\,\quad \left|z\right|>1$

${\begin{matrix}\operatorname {arccot} z&=&{\frac {\pi }{2}}-\arctan z\\&=&{\frac {\pi }{2}}-(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots )\\&=&{\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\end{matrix}}\,\quad \left|z\right|<1$

Tích Phân

Chúng cũng có thể được định nghĩa thông qua các biểu thức sau, dựa vào tính chất chúng là đạo hàm của các hàm khác.

$\arcsin \left(x\right)=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1$

$\arccos \left(x\right)=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1$

$\arctan \left(x\right)=\int _{0}^{x}{\frac {1}{1+z^{2}}}\,\mathrm {d} z,\quad \forall x\in \mathbb {R}$

$\operatorname {arccot} \left(x\right)=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,\mathrm {d} z,\quad z>0$

$\operatorname {arcsec} \left(x\right)=\int _{x}^{1}{\frac {1}{|z|{\sqrt {z^{2}-1}}}}\,\mathrm {d} z,\quad x>1$

$\operatorname {arccsc} \left(x\right)=\int _{x}^{\infty }{\frac {-1}{|z|{\sqrt {z^{2}-1}}}}\,\mathrm {d} z,\quad x>1$

Số Phức

Công thức trên cho phép mở rộng hàm lượng giác nghịch đảo ra cho các biến số phức|phức:

$\arcsin(z)=-i\log \left(i\left(z+{\sqrt {1-z^{2}}}\right)\right)$

$\arccos(z)=-i\log \left(z+{\sqrt {z^{2}-1}}\right)$

$\arctan(z)={\frac {i}{2}}\log \left({\frac {1-iz}{1+iz}}\right)$