Sách giải tích/Hàm số/Đồ thị hàm số

Đồ thị

Đồ Thị là một cách hiển thị Tọa độ của một điểm trên một mặt phẳng . Có hai loại đồ thị

1. Đồ thị trục $X,Y$
2. Đồ thị trục $R,\theta$

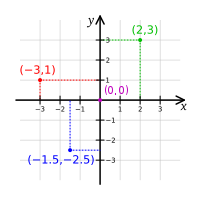
Đồ Thị trục xOy

Đồ Thị XY là một Đồ Thị tạo bởi hai đường thẳng vuông góc với nhau

Một ngang, gọi là trục hoành hay trục Ox ;

Một thẳng đứng, gọi là trục tung hay trục Oy

Cắt nhau tại một điểm, gọi là điểm gốc có tọa độ (0,0)

Một điểm, A , trên Đồ Thị XY sẽ có một

Tọa độ A(X,Y) với chiều dài X và độ cao Y

Thí dụ

Tọa độ của một điểm A(4,8) có x = 4 và y = 8

Đồ Thị Vòng Tròn

Đồ Thị Vòng Tròn là một cách hiển thị Tọa độ của một điểm trên vòng tròn có Bán kín R ở Góc độ θ

Khi một đường thẳng có độ dài R cắt đường chân trời (đường thẳng ngang) tại một điểm và tạo thành một góc θ. Trên mặt phẳng Rθ, đường bán kín R cắt đường chân trời tại một điểm gốc (R,0) . Trên mặt phẳng Rθ, Một điểm chuyển động theo vòng tròn sẻ có một tọa độ A(R,θ) và được biểu hiện như sau A = R/_θ

Chuyển Đổi Hệ Tọa Độ

Nếu có một điểm có tọa độ A(X,Y) tương đương với A(R,θ) trong Hệ số Thực thì

Giá trị của R và θ được tính từ giá trị của X và Y như sau

$R^{2}=X^{2}+Y^{2}$

$Tan\theta ={\frac {Y}{X}}$

Dưới dạng Hàm số lượng giác giá trị của X và Y được tính từ giá trị của R và θ như sau

$X(\theta )=RCos\theta$

$Y(\theta )=RSin\theta$

Đồ thị hàm số

Kẻ hình hàm số cho biết tương quan giửa 2 đại lượng x, y biểu thị bằng hàm sô

$y=x$

Lập bảng tương quan giửa hai giá trị x và y

x	-2	-1	0	1	2
y = x	-2	-1	0	1	2

Đặt điểm (x,y) trên đồ thi x-y ta có Đồ thị hàm số đường thẳng đi qua điểm gốc (0,0) có độ nghiêng bằng 1