Hàm số là một biểu thức đại số được dùng trong việc biểu diển tương quan giửa 2 đại lương với nhau . Thí dụ như
y
=
2
x
+
5
{\displaystyle y=2x+5}
Mọi hàm số của một biến số
f
(
x
)
{\displaystyle f(x)}
y
=
2
x
{\displaystyle y=2x}
Hàm số 2 biến số
f
(
x
,
y
)
{\displaystyle f(x,y)}
r
2
=
x
2
+
y
2
{\displaystyle r^{2}=x^{2}+y^{2}}
f
(
r
,
θ
)
{\displaystyle f(r,\theta )}
Z
∠
θ
=
(
x
2
+
y
2
)
∠
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {(}}x^{2}+y^{2})\angle tan^{-1}{\frac {y}{x}}}
Hàm số 3 biến số
f
(
x
,
y
,
z
)
{\displaystyle f(x,y,z)}
r
2
=
x
2
+
y
2
+
z
2
{\displaystyle r^{2}=x^{2}+y^{2}+z^{2}}
Mọi hàm số đều có một giá trị
Hàm số bằng không
f
(
x
)
=
0
{\displaystyle f(x)=0}
Hàm số bằng hằng số không đổi
f
(
x
)
=
C
{\displaystyle f(x)=C}
Hàm số khác không
f
(
x
)
=
y
(
x
)
{\displaystyle f(x)=y(x)}
Dạng hàm số Công thức Thí dụ
Hàm số tuần hoàn Periodic function
f
(
x
)
=
f
(
x
+
T
)
{\displaystyle f(x)=f(x+T)}
s
i
n
x
=
s
i
n
(
x
+
k
2
π
)
{\displaystyle sinx=sin(x+k2\pi )}
Hàm số chẳn even function
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
Hàm số lẽ odd function
f
(
x
)
=
−
f
(
x
)
{\displaystyle f(x)=-f(x)}
y
(
x
)
=
−
y
(
x
)
{\displaystyle y(x)=-y(x)}
Hàm số nghịch đảo inverse function
f
−
1
(
x
)
=
1
f
(
x
)
{\displaystyle f^{-1}(x)={\frac {1}{f(x)}}}
s
i
n
−
1
x
=
1
s
i
n
x
{\displaystyle sin^{-1}{x}={\frac {1}{sinx}}}
Hàm số trong hàm số composite function
f
(
x
)
=
f
(
g
(
x
)
)
{\displaystyle f(x)=f(g(x))}
Hàm số nhiều biến số parametric function
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Hàm số tương quan/]] recursive function
Hàm số chia/]] Rational function
Q
(
x
)
=
N
(
x
)
M
(
x
)
−
R
(
x
)
{\displaystyle Q(x)={\frac {N(x)}{M(x)}}-R(x)}
Đồ Thị là một cách hiển thị Tọa độ của một điểm trên một mặt phẳng . Có hai loại đồ thị đồ thị trục
X
,
Y
{\displaystyle X,Y}
R
,
θ
{\displaystyle R,\theta }
Đồ Thị XY là một Đồ Thị tạo bởi hai đường thẳng vuông góc với nhau
Một ngang, gọi là trục hoành hay trục Ox ;
Một thẳng đứng, gọi là trục tung hay trục Oy
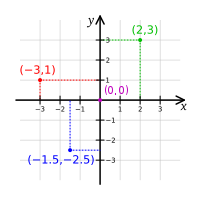
Cắt nhau tại một điểm, gọi là điểm gốc có tọa độ (0,0) Một điểm, A , trên Đồ Thị XY sẽ có một
Tọa độ A(X,Y) với chiều dài X và độ cao Y
Tọa độ của một điểm A(4,8) có x = 4 và y = 8 Đồ Thị Vòng Tròn là một cách hiển thị Tọa độ của một điểm trên vòng tròn có Bán kín R ở Góc độ θ
[ sửa ] Nếu có một điểm có tọa độ A(X,Y) tương đương với A(R,θ) trong Hệ số Thực thì
Giá trị của R và θ được tính từ giá trị của X và Y như sau
R
2
=
X
2
+
Y
2
{\displaystyle R^{2}=X^{2}+Y^{2}}
T
a
n
θ
=
Y
X
{\displaystyle Tan\theta ={\frac {Y}{X}}}
Dưới dạng Hàm số lượng giác giá trị của X và Y được tính từ giá trị của R và θ như sau
X
(
θ
)
=
R
C
o
s
θ
{\displaystyle X(\theta )=RCos\theta }
Y
(
θ
)
=
R
S
i
n
θ
{\displaystyle Y(\theta )=RSin\theta }
Kẻ hình hàm số cho biết tương quan giửa 2 đại lượng x, y biểu thị bằng hàm sô
y
=
x
{\displaystyle y=x}
Lập bảng tương quan giửa hai giá trị x và y
x -2
-1
0
1
2
y = x -2
-1
0
1
2
Đặt điểm (x,y) trên đồ thi x-y ta có Đồ thị hàm số đường thẳng đi qua điểm gốc (0,0) có độ nghiêng bằng 1
[ sửa ] Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
+
.
.
.
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
+
.
.
.
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}+...=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}+...}
Chứng minh Khi x=0
f
(
0
)
=
a
0
{\displaystyle f(0)=a_{0}}
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
f
′
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
4
a
4
x
3
{\displaystyle f^{'}(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+4a_{4}x^{3}}
f
′
(
0
)
=
a
1
{\displaystyle f^{'}(0)=a_{1}}
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
f
″
(
x
)
=
2
a
2
+
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
a
4
x
2
+
(
5
)
(
4
)
a
5
x
3
{\displaystyle f^{''}(x)=2a_{2}+(3)(2)a_{3}x+(4)(3)a_{4}x^{2}+(5)(4)a_{5}x^{3}}
f
″
(
0
)
=
2
a
2
{\displaystyle f^{''}(0)=2a_{2}}
a
2
=
f
″
(
0
)
2
{\displaystyle a_{2}={\frac {f^{''}(0)}{2}}}
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
f
‴
(
x
)
=
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
(
2
)
a
4
x
+
(
5
)
(
4
)
(
3
)
a
5
x
2
{\displaystyle f^{'''}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_{5}x^{2}}
f
‴
(
0
)
=
(
3
)
(
2
)
a
3
{\displaystyle f^{'''}(0)=(3)(2)a_{3}}
a
3
=
f
‴
(
0
)
3
!
{\displaystyle a_{3}={\frac {f^{'''}(0)}{3!}}}
Thế
a
0
,
a
−
1
,
a
−
2
{\displaystyle a_{0},a-1,a-2}
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}}
f
(
x
)
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
{\displaystyle f(x)=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}}
Thí dụ
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f(0)=\sin(0)=0}
f
″
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{''}(x)=-\sin(x)}
f
″
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{''}(0)=-\sin(0)=0}
f
‴
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{'''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
sin
(
x
)
=
0
+
x
(
1
)
+
x
2
2
!
(
0
)
+
x
3
3
!
(
−
1
)
+
x
5
5
!
(
1
)
=
x
−
x
3
3
!
+
x
5
5
!
{\displaystyle \sin(x)=0+x(1)+{\frac {x^{2}}{2!}}(0)+{\frac {x^{3}}{3!}}(-1)+{\frac {x^{5}}{5!}}(1)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
0
)
=
cos
(
0
)
=
1
{\displaystyle f(0)=\cos(0)=1}
f
′
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{'}(x)=-\sin(x)}
f
′
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{'}(0)=-\sin(0)=0}
f
″
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
f
‴
(
x
)
=
sin
(
x
)
{\displaystyle f^{'''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
cos
(
x
)
=
1
+
x
(
0
)
+
x
2
2
!
(
−
1
)
+
x
3
3
!
(
0
)
+
x
4
4
!
(
1
)
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
{\displaystyle \cos(x)=1+x(0)+{\frac {x^{2}}{2!}}(-1)+{\frac {x^{3}}{3!}}(0)+{\frac {x^{4}}{4!}}(1)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}}
Phương trình là một đẳng thức của một hàm số toán của 1 hay nhiều hơn một biến số có giá trị bằng không
f
(
x
)
=
0
{\displaystyle f(x)=0}
Với
x - Nghiệm số , mọi giá trị của x thỏa mản phương trình
f
(
x
)
=
0
{\displaystyle f(x)=0}
2
x
+
5
=
0
{\displaystyle 2x+5=0}
2
x
y
+
5
=
z
{\displaystyle 2xy+5=z}
x
2
+
4
x
−
12
=
0
{\displaystyle x^{2}+4x-12=0}
[ sửa ] Giải phương trình là cách thức tìm giá trị của biến số sao cho hàm số của biến số có giá trị bằng không . Giá trị của biến số thỏa mản điều kiện f(x)=0 được gọi là nghiệm số của phương trình
2
x
+
4
=
6
{\displaystyle 2x+4=6}
2
x
=
6
−
4
=
2
{\displaystyle 2x=6-4=2}
x
=
2
/
2
=
1
{\displaystyle x=2/2=1}
[ sửa ] Dạng tổng quát
a
x
+
b
=
0
{\displaystyle ax+b=0}
Giải phương trình
a
x
+
b
=
0
{\displaystyle ax+b=0}
x
+
b
a
=
0
{\displaystyle x+{\frac {b}{a}}=0}
Nghiệm số phương trình
x
=
−
b
a
{\displaystyle x=-{\frac {b}{a}}}
[ sửa ] [ sửa ] [ sửa ] Dạng tổng quát
X
2
+
Y
2
=
0
{\displaystyle X^{2}+Y^{2}=0}
Giải phương trình
X
=
−
Y
2
=
±
j
Y
{\displaystyle X={\sqrt {-Y^{2}}}=\pm jY}
Y
=
−
X
2
=
±
j
X
{\displaystyle Y={\sqrt {-X^{2}}}=\pm jX}
[ sửa ] Dạng tổng quát
X
+
j
Y
=
0
{\displaystyle X+jY=0}
Giải phương trình
X
=
−
j
Y
{\displaystyle X=-jY}
j
Y
=
−
X
{\displaystyle jY=-X}
Y
=
j
X
{\displaystyle Y=jX}
[ sửa ] Phương trình tuyến tính có dạng tổng quát
a
0
x
0
+
a
1
x
1
+
.
.
.
+
a
n
x
n
=
A
{\displaystyle a_{0}x_{0}+a_{1}x_{1}+...+a_{n}x_{n}=A}
[ sửa ] Với hệ phương trình đường thẳng co dạng tổng quát
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
d
x
+
e
y
=
f
{\displaystyle dx+ey=f}
x
+
b
a
y
=
c
a
{\displaystyle x+{\frac {b}{a}}y={\frac {c}{a}}}
x
+
e
d
y
=
f
d
{\displaystyle x+{\frac {e}{d}}y={\frac {f}{d}}}
Trừ 2 phương trình trên, ta được
(
b
a
−
e
d
)
×
y
=
(
c
a
−
f
d
)
{\displaystyle ({\frac {b}{a}}-{\frac {e}{d}})\times y=({\frac {c}{a}}-{\frac {f}{d}})}
Tìm giá trị nghiệm số y
y
=
(
c
a
−
f
d
)
(
b
a
−
e
d
)
{\displaystyle y={\frac {({\frac {c}{a}}-{\frac {f}{d}})}{({\frac {b}{a}}-{\frac {e}{d}})}}}
a
b
x
+
y
=
c
b
{\displaystyle {\frac {a}{b}}x+y={\frac {c}{b}}}
d
e
x
+
y
=
f
e
{\displaystyle {\frac {d}{e}}x+y={\frac {f}{e}}}
Trừ 2 phương trình trên, ta được
(
a
b
−
d
e
)
×
x
=
(
c
b
−
f
e
)
{\displaystyle ({\frac {a}{b}}-{\frac {d}{e}})\times x=({\frac {c}{b}}-{\frac {f}{e}})}
Tìm giá trị nghiệm số y
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
d
x
+
e
y
=
f
{\displaystyle dx+ey=f}
Có nghiệm 2 nghiệm số
x
=
(
c
b
−
f
e
)
(
a
b
−
d
e
)
{\displaystyle x={\frac {({\frac {c}{b}}-{\frac {f}{e}})}{({\frac {a}{b}}-{\frac {d}{e}})}}}
y
=
(
c
a
−
f
d
)
(
b
a
−
e
d
)
{\displaystyle y={\frac {({\frac {c}{a}}-{\frac {f}{d}})}{({\frac {b}{a}}-{\frac {e}{d}})}}}
2
x
+
3
y
=
4
{\displaystyle 2x+3y=4}
5
x
+
6
y
=
7
{\displaystyle 5x+6y=7}
Thế
a
=
2
,
b
=
3
,
c
=
4
,
d
=
5
,
e
=
6
,
f
=
7
{\displaystyle a=2,b=3,c=4,d=5,e=6,f=7}
x
=
(
c
b
−
f
e
)
(
a
b
−
d
e
)
{\displaystyle x={\frac {({\frac {c}{b}}-{\frac {f}{e}})}{({\frac {a}{b}}-{\frac {d}{e}})}}}
y
=
(
c
a
−
f
d
)
(
b
a
−
e
d
)
{\displaystyle y={\frac {({\frac {c}{a}}-{\frac {f}{d}})}{({\frac {b}{a}}-{\frac {e}{d}})}}}
Ta có
x
=
(
4
3
−
7
6
)
(
2
3
−
5
6
)
=
3
6
/
−
3
6
=
−
1
{\displaystyle x={\frac {({\frac {4}{3}}-{\frac {7}{6}})}{({\frac {2}{3}}-{\frac {5}{6}})}}={\frac {3}{6}}/-{\frac {3}{6}}=-1}
y
=
(
4
2
−
7
5
)
(
3
2
−
6
7
)
=
6
10
/
3
14
=
84
30
{\displaystyle y={\frac {({\frac {4}{2}}-{\frac {7}{5}})}{({\frac {3}{2}}-{\frac {6}{7}})}}={\frac {6}{10}}/{\frac {3}{14}}={\frac {84}{30}}}
[ sửa ] Hệ hai phương trình tuyến tính hai ẩn có dạng tổng quát
{
a
.
x
+
b
.
y
=
e
,
c
.
x
+
d
.
y
=
f
,
{\displaystyle {\begin{cases}a.x+b.y=e,\\c.x+d.y=f,\end{cases}}}
Giải phương trình cho nghiệm số
x
=
e
d
−
b
f
a
d
−
b
c
;
y
=
a
f
−
c
e
a
d
−
b
c
{\displaystyle x={\frac {ed-bf}{ad-bc}}\;\;;y={\frac {af-ce}{ad-bc}}}
[ sửa ] có các hệ số của các ẩn tạo thành ma trận:
A
=
[
a
b
c
d
]
.
{\displaystyle \mathbf {A} ={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}.}
[
x
y
]
.
{\displaystyle \mathbf {} {\begin{bmatrix}x\\y\\\end{bmatrix}}.}
[
e
f
]
.
{\displaystyle \mathbf {} {\begin{bmatrix}e\\f\\\end{bmatrix}}.}
[ sửa ] Định thức của A
A
=
[
a
b
c
d
]
{\displaystyle A={\begin{bmatrix}a&b\\c&d\end{bmatrix}}}
det (A )=ad -bc .
A
=
[
e
b
f
d
]
{\displaystyle A={\begin{bmatrix}e&b\\f&d\end{bmatrix}}}
det (X )=ed -bf .
Y
=
[
a
e
c
f
]
{\displaystyle Y={\begin{bmatrix}a&e\\c&f\end{bmatrix}}}
det (A )=af -cd .
x
=
X
A
;
y
=
Y
A
{\displaystyle x={\frac {X}{A}}\;\;;y={\frac {Y}{A}}}
x
=
e
d
−
b
f
a
d
−
b
c
;
y
=
a
f
−
c
e
a
d
−
b
c
{\displaystyle x={\frac {ed-bf}{ad-bc}}\;\;;y={\frac {af-ce}{ad-bc}}}
[ sửa ] Thay đổi biến số x
Δ
x
=
(
x
+
Δ
x
)
−
x
{\displaystyle \Delta x=(x+\Delta x)-x}
Thay đổi biến số y
Δ
y
=
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=\Delta f(x)=f(x+\Delta x)-f(x)}
Biến đổi hàm số tính bằng tỉ lệ thay đổi biến số y trên thay đổi biến số x
Δ
y
Δ
x
=
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}}
d
d
x
f
(
x
)
=
f
′
(
x
)
=
lim
Δ
x
→
0
∑
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
∑
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=f^{'}(x)=\lim _{\Delta x\to 0}\sum {\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}\sum {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)}
∫
f
(
x
)
d
x
=
lim
Δ
x
→
0
∑
(
f
(
x
)
+
Δ
f
(
x
)
2
)
Δ
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)dx=\lim _{\Delta x\rightarrow 0}\sum (f(x)+{\frac {\Delta f(x)}{2}})\Delta x=F(x)+C}