Sách toán ứng dụng

Vector

Vector đại diện cho đường thẳng có hướng . Vector có ký hiệu ${\vec {A}}$ và công thức toán sau

${\vec {A}}=A{\vec {a}}$

Với

${\vec {A}}=A{\vec {a}}$	Vector đường thẳng
$A={\frac {\vec {A}}{\vec {a}}}$	Đường dài đường thẳng
${\vec {a}}={\frac {\vec {A}}{A}}$	Vector đường thẳng 1 đơn vị

Thí dụ

Vector đường thẳng	Vector	Vector 1 đơn vị	Độ dài
Vector đường thẳng ngang	${\vec {X}}=X{\vec {i}}$	${\vec {i}}={\frac {\vec {X}}{X}}$	$X={\frac {\vec {X}}{\vec {i}}}$
Vector đường thẳng dọc	${\vec {Y}}=Y{\vec {j}}$	${\vec {j}}={\frac {\vec {Y}}{Y}}$	$Y={\frac {\vec {Y}}{\vec {j}}}$
Vector đường thẳng nghiêng	${\vec {Z}}=Z{\vec {k}}$	${\vec {k}}={\frac {\vec {Z}}{Z}}$	$Z={\frac {\vec {Z}}{\vec {k}}}$
Vector đường tròn	${\vec {R}}=R{\vec {r}}={\vec {Z}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}$	${\vec {r}}={\frac {\vec {R}}{R}}$	$R={\frac {\vec {R}}{\vec {r}}}$

Đường dài

Đường thẳng

Tương quan góc và cạnh trong tam giác vuông Pythago

${\frac {X}{Z}}=cos\theta$

${\frac {Y}{Z}}=sin\theta$

${\frac {1}{X}}=sec\theta$

${\frac {1}{Y}}=csc\theta$

${\frac {Y}{X}}=tan\theta$

${\frac {X}{Y}}=cot\theta$

Đường dài các đường thẳng trong tam giác vuông

Đường dài đường thẳng ngang

$X={\frac {Y}{Z}}=Zcos\theta =x-x_{o}=\Delta x$

Đường dài đường thẳng dọc

$Y=ZX=Zsin\theta =y-y_{o}=\Delta y$

Đường dài đường thẳng nghiêng hay Độ dóc đường thẳng nghiêng

$Z={\frac {Y}{X}}=tan\theta ={\frac {y-y_{o}}{x-x_{o}}}={\frac {\Delta y}{\Delta x}}={\sqrt {X^{2}+Y^{2}}}$

Góc độ nghiêng

$\theta =Tan^{-1}Z=Tan^{-1}{\frac {Y}{X}}$

Phương trình đường thẳng nghiêng

Đường thẳng nghiêng ở góc độ nghiêng

$Z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle Tan^{-1}{\frac {Y}{X}}$

Đường thẳng nghiêng có độ nghiêng

$Y=ZX$

Từ trên,

$y-y_{o}=Z(x-x_{o})$

$y=y_{o}+ZX$

$y_{o}=y-ZX$

$X={\frac {Y}{Z}}={\frac {y-y_{o}}{Z}}$

Diện tích dưới hình đường thẳng nghiêng

$S=X(y_{o}+{\frac {Y}{2}})=X(y_{o}+{\frac {ZX}{2}})=X(y-{\frac {ZX}{2}})=({\frac {y-y_{o}}{Z}})({\frac {2y_{o}+y-y_{o}}{a}})={\frac {y^{2}-y_{o}^{2}}{2Z}}$

$y^{2}=y_{o}^{2}+2SZ$

Vòng tròn

Vòng tròn có bán kín R=Z

$Z^{2}=X^{2}+Y^{2}$

Vòng tròn có bán kín R=1

$1=cos^{2}\theta +sin^{2}\theta$

$1=sec^{2}\theta +tan^{2}\theta$

$1=csc^{2}\theta +cot^{2}\theta$

Cung tròn

$\alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\omega -\omega _{o}}{t-t_{o}}}$

$\omega =\omega _{o}+\alpha t$

$\theta =\Delta t(\omega _{o}+{\frac {\Delta \omega }{\Delta t}})=\Delta t(\omega _{o}+{\frac {\alpha \Delta t}{\Delta t}})=\Delta t(\omega -{\frac {\alpha \Delta t}{\Delta t}})=({\frac {\omega ^{2}-\omega _{o}^{2}}{2\alpha }})$

Vòng cong

Độ nghiêng

$a={\frac {f(t+\Delta t)-f(t)}{(t+\Delta t)-t}}={\frac {\Delta f(t)}{\Delta t}}$

Diện tích dưới hình

$s=\Delta t[f(t)+{\frac {\Delta f(t)}{2}}]$

Khi $\Delta t->0$

$a(t)=\lim _{\Delta t\to 0}\sum {\frac {\Delta f(t)}{\Delta t}}={\frac {d}{dt}}f(t)=f^{'}(t)$

$s(t)=\lim _{\Delta t\rightarrow 0}\sum (f(t)+{\frac {\Delta f(t)}{2}})\Delta t=\int f(t)dt=F(t)+C$

Chuyển động

Chuyển động thẳng hàng

Chuyển động thẳng hàng là một loại chuyển động theo một đường thẳng không đổi hướng .

Với mọi chuyển động thẳng hàng di chuyển qua 2 điểm không có đổi hướng từ điểm $(t_{o},v_{o})$ đến điểm $(t,v)$ có gia tốc biến đổi được tính bằng tỉ lệ của thay đổi vận tốc theo thay đổi thời gian

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}$

Vậy, Vận tốc di chuyển

$v=v_{o}+a\Delta t$

Từ trên

$v_{o}=v-a\Delta t$

$\Delta t={\frac {v-v_{o}}{a}}$

$\Delta v=a\Delta t$

Đường dài di chuyển được tính bằng diện tích dưới hình v-t

$s=v_{o}\Delta t+{\frac {\Delta v}{2}}\Delta t=\Delta t(v_{o}+{\frac {\Delta v}{2}})$

$s=\Delta t(v_{o}+{\frac {a\Delta t}{2}})$

$s=\Delta t(v-{\frac {a\Delta t}{2}})$

$s=({\frac {v-v_{o}}{a}})({\frac {2v_{o}+v-v_{o}}{2}})={\frac {v^{2}-v_{o}^{2}}{2a}}$

Từ trên

$v^{2}=v_{o}^{2}+2as$

Chuyển động thẳng hàng ở Gia tốc khác không

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}$ $v=v_{o}+a\Delta t$ $s=\Delta t(v_{o}+{\frac {\Delta v}{2}})=\Delta t(v_{o}+{\frac {a\Delta t}{2}})=\Delta t(v-{\frac {a\Delta t}{2}})={\frac {v^{2}-v_{o}^{2}}{2a}}$

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}={\frac {v-0}{t-0}}={\frac {v}{t}}$ $v=at$ $s={\frac {1}{2}}vt$

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-0}}={\frac {\Delta v}{t}}$ $v=v_{o}+at$ $s=t(v_{o}+{\frac {\Delta v}{2}})$

Chuyển động thẳng hàng ở Gia tốc bằng không

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}=0$ $v=v_{o}$ $s=v_{o}t$

Chuyển động thẳng hàng ở Gia tốc là một hằng số không đổi

$a=-g$ $v=-gt$ $s=-gt^{2}$

Chuyển động tròn

Chuyển động xoay tròn

Chuyển động cung tròn có

Đường dài

$s=r\theta$

Vận tốc

$v=r\omega$

Gia tốc

$a=r\alpha$

Với

$\alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\omega -\omega _{o}}{t-t_{o}}}$

$\omega =\omega _{o}+\alpha t$

$\theta =\Delta t(\omega _{o}+{\frac {\Delta \omega }{\Delta t}})=\Delta t(\omega _{o}+{\frac {\alpha \Delta t}{\Delta t}})=\Delta t(\omega -{\frac {\alpha \Delta t}{\Delta t}})=({\frac {\omega ^{2}-\omega _{o}^{2}}{2\alpha }})$

Chuyển động quay tròn

Chuyển động trọn vòng tròn có

Đường dài

$s=2\pi$

Vận tốc

$v={\frac {s}{t}}={2\pi }{t}=2\pi f=\omega$

Gia tốc

$a={\frac {v}{t}}={\frac {\omega }{t}}$

Chuyển động cong

Chuyển động cong đại diện cho chuyển động không đều có thay đổi hướng di chuyển có gia tốc, vận tốc và đường dài di chuyển tính bằng bằng gia tốc tức thời $a(t)$ , vận tốc tức thời $v(t)$ và đường dài tức thời $s(t)$

Chuyển động cong v(t)

Gia tốc trung bình chuyển động cong

$a={\frac {v(t+\Delta t)-v(t)}{(t+\Delta t)-t}}={\frac {\Delta v(t)}{\Delta t}}$

$s=\Delta t[v(t)+{\frac {\Delta v(t)}{2}}]$

Khi $\Delta t->0$

Gia tốc túc thời chuyển động cong

$a=a(t)=\lim _{\Delta t\to 0}\sum {\frac {\Delta v(t)}{\Delta t}}={\frac {d}{dt}}v(t)=v^{'}(t)$

Vận tốc túc thời chuyển động cong

$v=v(t)$

Đường dài túc thời chuyển động cong

$s=s(t)=\lim _{\Delta t\rightarrow 0}\sum (v(t)+{\frac {\Delta v(t)}{2}})\Delta t=\int v(t)dt=V(t)+C$

Chuyển động cong s(t)

$a=v(t)={\frac {d}{dt}}v={\frac {d}{dt}}{\frac {d}{dt}}s(t)={\frac {d^{2}}{dt^{2}}}s(t)$

$v=v(t)={\frac {d}{dt}}s(t)$

$s=s(t)$

Từ trên,

Chuyển Động		v	a	s
Cong		$v(t)$	${\frac {d}{dt}}v(t)$	$\int v(t)dt$
Thẳng nghiêng		$at+v$	$a$	${\frac {1}{2}}at^{2}+vt+C$
Thẳng nghiêng		$at$	$a$	${\frac {at^{2}}{2}}+$
Thẳng ngang		$v$	$0$	$vt$
Thẳng dọc		$t$	$1$	${\frac {t^{2}}{2}}$

Chuyển Động		s	v	a
Cong		$s(t)$	${\frac {d}{dt}}s(t)$	${\frac {d^{2}}{dt^{2}}}s(t)$
Vector đương thẳng ngang	→→	${\vec {X}}=X{\vec {i}}$	${\frac {d}{dt}}{\vec {X}}={\frac {dX}{dt}}{\vec {i}}=v_{x}{\vec {i}}$	${\frac {d^{2}}{dt^{2}}}{\vec {X}}={\frac {d^{2}X}{dt^{2}}}{\vec {i}}=a_{x}{\vec {i}}$
Vector đương thẳng dọc	↑ ↑	${\vec {Y}}=Y{\vec {j}}$	${\frac {d}{dt}}{\vec {Y}}={\frac {dY}{dt}}{\vec {j}}=v_{y}{\vec {j}}$	${\frac {d^{2}}{dt^{2}}}{\vec {Y}}={\frac {d^{2}Y}{dt^{2}}}{\vec {j}}=a_{y}{\vec {j}}$
Vector đương thẳng nghiêng		${\vec {Z}}=Z{\vec {k}}$	${\frac {d}{dt}}{\vec {Z}}={\frac {dZ}{dt}}{\vec {k}}=v_{z}{\vec {k}}$	${\frac {d^{2}}{dt^{2}}}{\vec {Z}}={\frac {d^{2}Z}{dt^{2}}}{\vec {k}}=a_{z}{\vec {k}}$
Vector đương tròn		${\vec {R}}=R{\vec {r}}$	${\frac {d}{dt}}{\vec {R}}$ $R{\frac {d}{dt}}{\vec {r}}+{\vec {r}}{\frac {d}{dt}}R=R{\frac {d}{dt}}{\vec {r}}$	${\frac {d^{2}}{dt^{2}}}{\vec {R}}$ $R{\frac {d^{2}}{dt^{2}}}{\vec {r}}+{\vec {r}}{\frac {d^{2}}{dt^{2}}}R=R{\frac {d^{2}}{dt^{2}}}{\vec {r}}$
Vector đương tròn		${\vec {R}}={\vec {X}}+{\vec {Y}}$	${\frac {d}{dt}}{\vec {R}}={\frac {d}{dt}}({\vec {X}}+{\vec {Y}})$ ${\frac {dX}{dt}}{\vec {i}}+{\frac {dY}{dt}}{\vec {j}}=v_{x}{\vec {i}}+v_{y}{\vec {j}}$	${\frac {d^{2}}{dt^{2}}}{\vec {R}}={\frac {d^{2}}{dt^{2}}}({\vec {X}}+{\vec {Y}})$ ${\frac {d^{2}X}{dt^{2}}}{\vec {i}}+{\frac {d^{2}Y}{dt^{2}}}{\vec {j}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}$

Chuyển động sóng

Phương trình sóng và Hàm số sóng

Với phương trình sóng có dạng tổng quát

$af^{n}(t)+bf(t)=0$

Dùng hoán chuyển Laplace , ta có

$s^{n}f(t)=-{\frac {b}{a}}f(t)$

$s^{n}=-{\frac {b}{a}}$

$s={\sqrt[{n}]{-{\frac {b}{a}}}}=\pm j{\sqrt[{n}]{\frac {b}{a}}}=\pm j\omega$

$f(t)=Ae^{st}=Ae^{\pm j\omega t}=Asin\omega t$

$\omega ={\sqrt[{n}]{\frac {b}{a}}}$ Sao cho n ≥ 2

Sóng sin có thể biểu diển bằng Hàm số sóng sau

$f(t)=Asin\omega t$

Hàm số sóng này thỏa mản một Phương trình sóng sau

$f^{n}(t)=-\beta f(t)$

Với

$\omega ={\sqrt[{n}]{\beta }}$

n ≥ 2

Nhiệt

Nhiệt độ

Nhiệt độ chuẩn

Nhiệt độ phòng	$25^{o}C$
Nhiệt độ đông đặc	$0^{o}C$
Nhiệt độ tan lỏng	$25^{o}C$
Nhiệt độ bốc hơi	$100^{o}C$

Nhiệt và vật

Nhiệt điện từ

≈≈≈ || ≈≈≈==|| ≈≈≈e

Nhiệt điện từ	Nhiệt	Nhiệt quang	Nhiệt điện
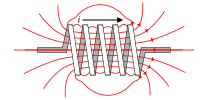
Lối mắc	Cộng dây thẳng dẫn điện	Cuộn tròn của N vòng tròn dẫn điện	Cuộn tròn của N vòng tròn dẫn điện với từ vật nằm trong các vòng quấn
Tần số thời gian	$f<f_{o}$	$f=f_{o}$	$f>f_{o}$
Năng lực nhiệt	$W=pv=mC\Delta T$	$W_{o}=pv=pC=hf_{o}$	$W=pv=pC=hf$
Hằng số C	$C=p{\frac {v}{m\Delta T}}$	$C={\sqrt {\frac {1}{\mu _{o}\epsilon _{o}}}}=\omega _{o}=\lambda _{o}f_{o}$	$C={\sqrt {\frac {1}{\mu \epsilon }}}=\omega =\lambda f$
Khối lượng/Lượng tử	$m=p\lambda =p{\frac {C\Delta T}{v}}$	$h=p\lambda _{o}$	$h=p\lambda$
Động lượng	$p={\frac {m}{\lambda }}=m{\frac {v}{C\Delta T}}$	$p={\frac {h}{\lambda _{o}}}$	$p={\frac {h}{\lambda }}$
Bước sóng	$\lambda ={\frac {m}{p}}={\frac {C\Delta T}{v}}$	$\lambda _{o}={\frac {C}{f_{o}}}={\frac {h}{p}}$	$\lambda ={\frac {C}{f}}={\frac {h}{p}}$

Nhiệt Phóng xạ sóng điện từ

Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T}}B$
$T=\mu \epsilon$

Cho một Phương trình sóng điện từ

$\nabla ^{2}E=-\beta E$

$\nabla ^{2}B=-\beta B$

$\omega ={\sqrt {\beta }}$

Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ

$E=ASin\omega t$

$B=ASin\omega t$

Với

$\omega =\lambda f={\sqrt {\beta }}={\sqrt {\frac {1}{T}}}=C$

$T=\mu \epsilon$

Nhiệt tỏa vào môi trường xung quanh của cuộn từ được biểu diển bằng phóng xạ sóng điện từ như sau

$W=pv=p\omega =p\lambda f=hf=pC$

$h=p\lambda$

$p={\frac {h}{\lambda }}$

$\lambda ={\frac {h}{p}}={\frac {c}{f}}$

Nhiệt Phóng xạ vật đen

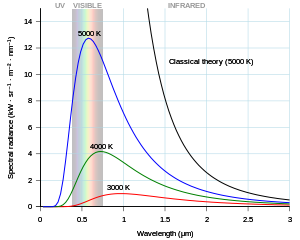
Định luật Planck (minh họa bằng các đường cong màu) miêu tả chính xác bức xạ vật đen và giải quyết vấn đề "thảm họa cực tím" (đường màu đen).

Định luật Planck miêu tả bức xạ điện từ phát ra từ vật đen trong trạng thái cân bằng nhiệt ở một nhiệt độ xác định. Định luật đặt tên theo Max Planck, nhà vật lý đã nêu ra nó vào năm 1900. Định luật này là bước đi tiên phong đầu tiên của vật lý hiện đại và cơ học lượng tử.

Đối với tần số ν, hoặc bước sóng λ, định luật Planck viết dưới dạng:

$B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\mathrm {B} }T}}-1}}$

hoặc

$B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}$

Với

B ký hiệu của cường độ bức xạ (spectral radiance),

T là nhiệt độ tuyệt đối, kB là hằng số Boltzmann,

h là hằng số Planck, và c là tốc độ ánh sáng trong môi trường hoặc trong chân không.

[1][2][3] Đơn vị SI của phương trình là W·sr−1·m−2·Hz−1 đối với Bν(T) và W·sr−1·m−3 đối với Bλ(T).

Nhiệt phân rả nguyên tố

$Ur=Th+X$

$C=N+Y$

$UrTh+X$

Nhiệt phân rả nguyên tử

$hf=hf_{o}+{\frac {1}{2}}mv^{2}$

$nhf=2\pi rmv$

Nhiệt truyền

Nhiệt dẩn

$W=pv=mv\Delta T$

$T_{1}=T_{2}$

$\Delta T=T_{1}-T_{2}=0$

$W=mv\Delta T=0$

$T_{1}>T_{2}$

$\Delta T=T_{1}-T_{2}$

$W=mv\Delta T=mv(T_{1}-T_{2})$

$T_{1}-->T_{2}$

$T_{2}>T_{1}$

$\Delta T=T_{2}-T_{1}$

$W=mv\Delta T=mv(T_{2}-T_{1})$

$T_{1}<--T_{2}$

Nhiệt phóng xạ

$W=\phi +KE=hf$

Ở $f=f_{o}$

$KE=0$

Vậy,

$\phi =hf_{o}$

Nhiệt phân rả

Từ

$W=\phi +KE=hf$

Ta có

$hf=hf_{o}+{\frac {1}{2}}mv^{2}$

Điện

Điện nguồn

Điện DC

$I={\frac {Q}{t}}$
$Q=It$
$V={\frac {W}{Q}}$
$W=QV$
$U={\frac {W}{t}}={\frac {QV}{t}}=IV$

Điện AC

$i(t)={\frac {d}{dt}}Q(t)$
$Q(t)=\int i(t)dt$
$v(t)={\frac {d}{dt}}{\frac {W(t)}{Q(t)}}$
$W(t)=\int v(t)dQ(t)dt=\int v(t)i(t)dt$
$U(t)={\frac {d}{dt}}W(t)={\frac {d}{dt}}\int v(t)i(t)dt$

Điện trở

Điện DC

$R={\frac {V}{I}}$
$V=IR$
$I={\frac {V}{R}}$
$P=IV=I^{2}R={\frac {V^{2}}{R}}$

Điện AC

$i(t)={\frac {v(t)}{X}}$
$v(t)=i(t)X$
$X={\frac {v(t)}{i(t)}}=0$
$Z=R+X=R\angle 0=R=r$

$B=Li={\frac {\mu }{2\pi r}}i$

$L={\frac {B}{i}}={\frac {\mu }{2\pi r}}$

$W_{i}=i^{2}R(T)$

$R(T)=R_{o}+nT$

$R(T)=R_{o}e^{nT}$

$W_{e}=pv=mC\Delta T$

Cuộn từ

Điện DC

$B=LI$
$L={\frac {B}{I}}$
$I={\frac {B}{L}}$

Điện AC

$v(t)=L{\frac {d}{dt}}i(t)$
$i(t)={\frac {1}{L}}\int v(t)dt$
$X={\frac {v(t)}{i(t)}}=\omega L\angle 90=j\omega L=sL$
$Z=R+X=R+{\frac {v(t)}{i(t)}}=R\angle 0+\omega L\angle 90=R+j\omega L=R+sL$

Với H=0

$B=Li={\frac {N\mu _{o}}{l}}i$

$L={\frac {B}{i}}={\frac {N\mu _{o}}{l}}$

$W_{i}=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}$

$W_{e}=pC=hf_{o}$

Với H≠0

$B=Li={\frac {N\mu }{l}}i$

$L={\frac {B}{i}}={\frac {N\mu }{l}}$

$W_{i}=W_{H}+W_{B}=i^{2}R(T)+{\frac {1}{2}}Li^{2}$

$W_{e}=pC=hf$

Tụ điện

Điện DC

$Q=CV=CEl$
$C={\frac {Q}{V}}$
$V={\frac {Q}{C}}$

$E={\frac {V}{l}}={\frac {Q}{Cl}}$

Điện AC

$v(t)={\frac {1}{C}}\int i(t)dt$
$i(t)=C{\frac {d}{dt}}v(t)$
$X={\frac {v(t)}{i(t)}}={\frac {1}{\omega C}}\angle -90={\frac {1}{j\omega C}}={\frac {1}{SC}}$
$Z=R+X=R+{\frac {v(t)}{i(t)}}=R\angle 0+{\frac {1}{\omega C}}\angle -90=R+{\frac {1}{j\omega C}}=R+{\frac {1}{SC}}$

Điện từ

Mật độ điện trường và từ trường

Định luật Gauss cho biết cách tính mật độ điện trường và từ trường

Ψ_E = EA = $\oint \mathbf {E} \cdot d\mathbf {A} ={1 \over \epsilon _{o}}\int _{V}\rho \ dV={\frac {Q}{\epsilon _{o}}}$

Ψ_B = BA = $\oint \mathbf {B} \cdot d\mathbf {A} =\mu I$

Với

$\Phi$ là thông lượng điện,

$\mathbf {E}$ là điện trường,

$d\mathbf {A}$ là diện tích của một hình vuông vi phân trên mặt đóng S,

$Q_{\mathrm {A} }$ là điện tích được bao bởi mặt đó,

$\rho$ là mật độ điện tích tại một điểm trong

$V$, $\epsilon _{o}$ là hằng số điện của không gian tự do và $\oint _{S}$ là tích phân trên mặt S bao phủ thể tích V.

Mật độ điện trường

$E={\frac {\phi _{E}}{A}}={\frac {Q}{\epsilon A}}={\frac {D}{\epsilon }}$

Mật độ từ trường

$B={\frac {\phi _{B}}{A}}={\frac {\mu }{A}}I=LI=\mu H$

Phương trình Điện từ nhiểm Maxwell

Tên	Dạng vi phân	Dạng tích phân
Định luật Gauss:	$\nabla \cdot \mathbf {D} =\rho$	$\oint _{S}\mathbf {D} \cdot d\mathbf {A} =\int _{V}\rho dV$
Đinh luật Gauss cho từ trường (sự không tồn tại của từ tích):	$\nabla \cdot \mathbf {B} =0$	$\oint _{S}\mathbf {B} \cdot d\mathbf {A} =0$
Định luật Faraday cho từ trường:	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	$\oint _{C}\mathbf {E} \cdot d\mathbf {l} =-\ {d \over dt}\int _{S}\mathbf {B} \cdot d\mathbf {A} =-{\frac {d\phi }{dt}}$
Định luật Ampere (với sự bổ sung của Maxwell):	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$	$\oint _{C}\mathbf {H} \cdot d\mathbf {l} =\int _{S}\mathbf {J} \cdot d\mathbf {A} +{d \over dt}\int _{S}\mathbf {D} \cdot d\mathbf {A} =\mu _{o}I+\epsilon _{o}\mu _{o}{\frac {d\phi _{E}}{dt}}$

Phương trình Sóng Điện từ Laplace

Phương trình vector sóng điện từ

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T}}B$
$T=\mu \epsilon$

Phương trình sóng điện từ

$\nabla ^{2}E=-\beta E$

$\nabla ^{2}B=-\beta B$

Hàm số sóng điện từ

$E=Asin\omega t$

$B=Asin\omega t$

$\omega ={\sqrt {\beta }}={\sqrt {\frac {1}{T}}}={\sqrt {\frac {1}{\mu \epsilon }}}=C$

Lượng tử

Phương trình Schrödinger

Phương trình Schrödinger là một phương trình cơ bản của vật lý lượng tử mô tả sự biến đổi trạng thái lượng tử của một hệ vật lý theo thời gian, thay thế cho các định luật Newton và biến đổi Galileo trong cơ học cổ điển.

Trong cơ học lượng tử, trạng thái lượng tử của một hệ vật lý được mô tả đầy đủ nhất bởi một vector trạng thái thí dụ như hàm sóng trong không gian cấu hình, nghiệm của phương trình Schrödinger. Nghiệm của phương trình Schrödinger không chỉ mô tả các hệ nguyên tử và hạ nguyên tử (nguyên tử, phân tử, hạt nhân, điện tử và các hạt cơ bản khác) mà cả các hệ vĩ mô, thậm chí có thể là toàn bộ Vũ trụ. Phương trình này được đặt tên theo nhà vật lý người Áo Erwin Schrödinger, người đã lần đầu tiên thiết lập nó vào năm 1926.

$i\hbar {\frac {\partial \psi }{\partial t}}=\left(-{\frac {\hbar ^{2}}{2m}}\Delta ^{2}+V\right)\psi$

Phương trình Schrödinger có nhiều dạng khác nhau, tùy thuộc vào các điều kiện khác nhau của hệ vật lý. Mục này nhằm mục đích giới thiệu phương trình Schrödinger cho trường hợp tổng quát và cho các trường hợp đơn giản hơn thường gặp.

Hệ lượng tử tổng quát

Đối với một hệ lượng tử tổng quát:

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)={\hat {H}}\Psi (\mathbf {r} ,t)$

trong đó

• $i$ là đơn vị ảo
• $\Psi (\mathbf {r} ,t)$ là hàm sóng, biên độ xác suất cho các cấu hình khác nhau của hệ
• $\hbar$ là hằng số Planck thu gọn (thường được chuẩn hóa về đơn vị trong các hệ đơn vị tự nhiên)
• ${\hat {H}}$ là toán tử Hamilton.

Trường hợp một hạt trong không gian ba chiều

Đối với một hệ gồm một hạt trong ba chiều:

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,\,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,\,t)$

trong đó

• $\mathbf {r} =(x,y,z)$ là tọa độ của hạt trong không gian ba chiều,
• $\Psi (\mathbf {r} ,t)$ là hàm sóng, biên độ xác suất để hạt có một tọa độ xác định r ở một thời điểm xác định bất kì t.
• $m$ là khối lượng của hạt.
• $V(\mathbf {r} )$ là thế năng không phụ thuộc thời gian của hạt ở tọa độ r.
• $\nabla ^{2}$ là toán tử Laplace.

Xây dựng phương trình

Các giả thiết

(1)Năng lượng toàn phần E của một hạt

$E=T+V={\frac {p^{2}}{2m}}+V$

Đây là biểu thức cổ điển cho một hạt có khối lượng m trong đó năng lượng toàn phần E là tổng của động năng, $T={\frac {p^{2}}{2m}}$, và thế năng V. Xung lượng của hạt là p, hay tích của khối lượng và vận tốc. Thế năng là một hàm biến đổi theo vị trí và cũng có thể biến đổi cả theo thời gian.

Chú ý rằng năng lượng E và xung lượng p xuất hiện trong các hệ thức sau:

(2) Giả thuyết về lượng tử ánh sáng của Max Planck năm 1905, khẳng định rằng năng lượng của một photon tỷ lệ với tần số của sóng điện từ tương ứng:

$E=hf={h \over 2\pi }(2\pi f)=\hbar \omega \;$

trong đó tần số f và năng lượng E của lượng tử ánh sáng (photon) được liên hệ bởi hăng số Planck h,

và $\omega =2\pi f\;$ là tần số góc của sóng.

(3) Giả thuyết de Broglie năm 1924, phát biểu rằng bất kì một hạt nào cũng có thể liên quan đến một sóng, được biểu diễn một cách toán học bởi hàm sóng Ψ, và xung lượng p của hạt được liên hệ với bước sóng λ của sóng liên kết bởi hệ thức:

$p={h \over \lambda }={h \over 2\pi }{2\pi \over \lambda }=\hbar k\;$

trong đó $\lambda \,$ là bước sóng và $k=2\pi /\lambda \;$ là hằng số sóng hay số sóng góc.

Biểu diễn p and k như là những vector, chúng ta có

$\mathbf {p} =\hbar \mathbf {k} \;$

(4) Giả thiết rằng phương trình sóng phải là tuyến tính. Ba giả thuyết ở trên cho phép chúng ta có thể xây dựng được phương trình cho các sóng phẳng. Để kết luận rằng phương trình đó cũng đúng cho một trường hợp tổng quát bất kì đòi hỏi hàm sóng phải tuân theo nguyên lý chồng chất trạng thái.

Phương trình cho sóng phẳng đơn sắc

Schrödinger đã có một cách nhìn sâu sắc, vào cuối năm 1925, đó là phải biểu diễn pha của một sóng phẳng như là một thừa số pha phức:

$\Psi (\mathbf {x} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {x} -\omega t)}$

và nhận ra rằng vì

${\frac {\partial }{\partial t}}\Psi =-i\omega \Psi$

nên

$E\Psi =\hbar \omega \Psi =i\hbar {\frac {\partial }{\partial t}}\Psi$

và tương tự vì

${\frac {\partial }{\partial x}}\Psi =ik_{x}\Psi$

và

${\frac {\partial ^{2}}{\partial x^{2}}}\Psi =-k_{x}^{2}\Psi$

chúng ta tìm ra:

$p_{x}^{2}\Psi =(\hbar k_{x})^{2}\Psi =-\hbar ^{2}{\frac {\partial ^{2}}{\partial x^{2}}}\Psi$

do đó, đối với sóng phẳng, ta được:

$p^{2}\Psi =(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})\Psi =-\hbar ^{2}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)\Psi =-\hbar ^{2}\nabla ^{2}\Psi$

Và bằng cách thế những biểu thức cho năng lượng và xung lượng này vào công thức cổ điển $E={\frac {p^{2}}{2m}}+V$ chúng ta thu được phương trình nổi tiếng của Schrödinger cho trường hợp một hạt trong không gian ba chiều với sự có mặt của một trường thế năng V:

$i\hbar {\frac {\partial }{\partial t}}\Psi =-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +V\Psi$

Phương trình này đã được tổng quát hóa thành một tiên đề của cơ học lượng tử, nghĩa là coi nó là đúng cho mọi trường hợp mà không thể chứng minh được bằng lý thuyết mà chỉ có thể kiểm chứng bằng thực nghiệm. Phương trình Schrödinger đã đưa ra được nhiều tiên đoán phù hợp với thực tế và được kiểm định là đúng cho vô số trường hợp khác nhau.