Sách giải tích/Ứng dụng toán giải tích
Giao diện
Toán chuyển động
[sửa]Chuyển động v(t)
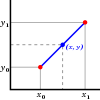
[sửa]Vector chuyển động
[sửa]Chuyển Động s v a Thẳng ngang → Thẳng dọc ↑ Thẳng nghiêng
Dao động sóng sin đều
[sửa]Dao động lò xo lên xuống
Dao động lò xo qua lại
Dao động đong đưa con lắc
Toán Điện từ
[sửa]Định luật điện từ
[sửa]Các Định luật điện từ được phát triển bởi nhiều nhà khoa học gia
Định luật Gauss Từ thông
Định luật Ampere Từ cảm Định luật Lentz Từ cảm ứng Định luật Faraday Điện từ cảm ứng Định luật Maxwell Từ nhiểm Định luật Maxwell-Ampere Dòng điện
Phương trình Điện từ Maxwell
[sửa]Các phương trình Maxwell bao gồm bốn phương trình, đề ra bởi James Clerk Maxwell, dùng để mô tả trường điện từ cũng như những tương tác của chúng đối với vật chất. Bốn phương trình Maxwell mô tả lần lượt:
- Điện tích tạo ra điện trường như thế nào (định luật Gauss).
- Sự không tồn tại của vật chất từ tích.
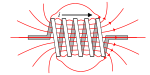
- Dòng điện tạo ra từ trường như thế nào (định luật Ampere).
- Và từ trường tạo ra điện trường như thế nào (định luật cảm ứng Faraday)
Tên Dạng phương trình vi phân Dạng tích phân Định luật Gauss: Đinh luật Gauss cho từ trường
(sự không tồn tại của từ tích):Định luật Faraday cho từ trường: Định luật Ampere
(với sự bổ sung của Maxwell):
Phương trình và hàm số Sóng Điện từ
[sửa]Vector trường điện từ
Phương trình hàm số Sóng Điện từ
Hàm số Sóng Điện từ
Toán Điện nhiệt
[sửa]Nhiệt nội
[sửa]Điện trở Cuộn từ Tụ điện
Nhiệt ngoại
[sửa]Điện trở Cuộn từ Với H=0 Cuộn từ Với H≠0