Sách giải tích/Đạo hàm
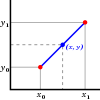
Đạo Hàm là một phép toán giải tích dùng trong việc tìm tổng biến đổi hàm số toán f(x) trên các khoảng thời gian ∆x = x - xo càng nhỏ gần như không. Một định nghỉa khác là phép toán tìm độ dóc của một hình có hàm số toán f(x)
Tính chất
[sửa]Ký hiệu
[sửa]Phép toán đạo hàm của hàm số có các dạng ký hiệu sau
Ký hiệu Chuẩn
- .
Ký hiệu Leibitz
Phép toán
[sửa]Với mọi hàm số f(x), đạo hàm của hàm số được tính theo công thức bên dưới
Với
Thay đổi biến số y
Thay đổi biến số x
Biến số hàm số
Tổng biến số hàm số
Giới hạn tổng biến số hàm số
Đạo hàm hàm số
Thí dụ
[sửa]Trong chuyển động biểu diểu bằng hàm số của vận tốc theo thời gian v(t) . Gia tốc chuyển động được tính như ở bên dưới
Trong chuyển động biểu diểu bằng hàm số của đường dài theo thời gian s(t) . Vận tốc chuyển động được tính như ở bên dưới
Công thức toán đạo hàm
[sửa]Hàm số , f(x) Đạo hàm hàm số f'(x) Giá trị Đạo hàm hằng số Đạo hàm tích hằng số với biến số Đạo hàm lũy thừa x Đạo hàm lũy thừa x Đạo hàm lũy thừa e Đạo hàm lũy thừa n Đạo hàm Ln
Quy luật toán đạo hàm
[sửa]Hoán chuyển đạo hàm
[sửa]Phép toán
[sửa]Hoán chuyển đạo hàm được thực hiện như sau
Hoán chuyển Ký hiệu Hoán chuyển Laplace Hoán chuyển Fourier Toán Đạo hàm Toán Đạo hàm hàm số
Giải phương trình đạo hàm
[sửa]Phương trình đạo hàm bậc nhứt - Phương trình phân hủy
[sửa]Với phương trình đạo hàm có dạng tổng quát
Dùng hoán chuyển đạo hàm ta có
Phương trình đạo hàm bậc hai - Phương trình sóng sin không đều
[sửa]Với phương trình đạo hàm có dạng tổng quát
Dùng hoán chuyển đạo hàm ta có
Giải phương trình đạo hàm
= < >
Phương trình đạo hàm bậc hai - Phương trình sóng sin đều
[sửa]Với phương trình đạo hàm có dạng tổng quát
Dùng hoán chuyển đạo hàm ta có
Giải phương trình đạo hàm
- . Với ≥ 2
Phương trình đạo hàm bậc n - Phương trình sóng ngắn
[sửa]Với phương trình đạo hàm có dạng tổng quát
Dùng hoán chuyển đạo hàm ta có




























































































![{\displaystyle {\frac {d}{dx}}[f(x)+g(x)]={\frac {d}{dx}}f(x)+{\frac {d}{dx}}g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf9a4c4bbbfe2b4af2bdb6e1c3a449b3765dd91)

![{\displaystyle {\frac {d}{dx}}[f(x)-g(x)]={\frac {d}{dx}}f(x)-{\frac {d}{dx}}g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1b346de22da31af2af82507751e920af862ef0)

![{\displaystyle {\frac {d}{dx}}[f(x)\times g(x)]=g(x){\frac {d}{dx}}f(x)+f(x){\frac {d}{dx}}g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9249e023ce1a2c9e66343c7faacae35ad69bfd63)

![{\displaystyle {\frac {d}{dx}}[f(x)/g(x)]={\frac {g(x){\frac {d}{dx}}f(x)+f(x){\frac {d}{dx}}g(x)}{g(x)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98858d11f7580550fa906e9b1cb4a092781faed0)












































![{\displaystyle s={\sqrt[{n}]{-{\frac {b}{a}}}}=\pm j{\sqrt[{n}]{\frac {b}{a}}}=\pm j\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7752ec47b3deeca8c652d36e0e194cc0f38c49dd)

![{\displaystyle \omega ={\sqrt[{n}]{\frac {b}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8cf316e30d63e6220cc3e62be9184edd423b96e)