Số đại số [ sửa ] Toán đại số dùng chữ cái a-z, A-Z đại diện cho các con số số học từ 0 đến 9. Thí dụ như A = 3 , B = 2 . Các chữ cái đại diện cho các con số số học được gọi là Biến số.
Loai số đại số [ sửa ] Số đại số được phân loai thành các loại số dưới đây
Loai số loại số Định nghỉa Ký hiệu Thí dụ
Số tự nhiên
N
{\displaystyle N}
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle 0,1,2,3,4,5,6,7,8,9}
Số chẳn Mọi số chia hết cho 2
2
n
{\displaystyle 2n}
2
,
4
,
6
,
{\displaystyle 2,4,6,}
Số lẻ Mọi số không chia hết cho 2
2
n
+
1
{\displaystyle 2n+1}
1
,
3
,
5
,
7
,
9
{\displaystyle 1,3,5,7,9}
Số nguyên tố Mọi số chia hết cho 1 và cho chính nó
p
{\displaystyle p}
1
,
3
,
5
,
7
{\displaystyle 1,3,5,7}
Số lũy thừa
a
n
=
a
×
a
×
a
.
.
.
×
a
{\displaystyle a^{n}=a\times a\times a...\times a}
a
n
{\displaystyle a^{n}}
2
3
=
2
×
2
×
2
=
8
{\displaystyle 2^{3}=2\times 2\times 2=8}
Số căn
n
a
{\displaystyle n{\sqrt {a}}}
a
1
n
{\displaystyle a^{\frac {1}{n}}}
n
a
{\displaystyle n{\sqrt {a}}}
a
1
n
{\displaystyle a^{\frac {1}{n}}}
Số log
L
o
g
a
b
=
c
{\displaystyle Log_{a}b=c}
a
c
=
b
{\displaystyle a^{c}=b}
L
o
g
a
b
{\displaystyle Log_{a}b}
L
o
g
10
100
=
2
{\displaystyle Log_{10}100=2}
Số nguyên
I
=
+
I
,
−
I
,
0
{\displaystyle I=+I,-I,0}
I
{\displaystyle I}
+
1
,
−
1
,
0
{\displaystyle +1,-1,0}
Phân số Số có dạng một số trên một số khác
a
b
{\displaystyle {\frac {a}{b}}}
1
2
{\displaystyle {\frac {1}{2}}}
Số thập phân
0.
a
b
c
d
{\displaystyle 0.abcd}
0.5
{\displaystyle 0.5}
Số hửu tỉ
Số vô tỉ
Số phức
Z
=
a
±
j
b
{\displaystyle Z=a\pm jb}
Z
{\displaystyle Z}
2
±
j
3
{\displaystyle 2\pm j3}
Số thực
a
{\displaystyle a}
a
{\displaystyle a}
2
{\displaystyle 2}
Số ảo
j
/
i
=
−
1
{\displaystyle j/i={\sqrt {-1}}}
i
,
j
{\displaystyle i,j}
±
j
3
{\displaystyle \pm j3}
Hằng số Số đại số có giá trị không đổi
c
{\displaystyle c}
π
,
e
{\displaystyle \pi ,e}
Phép toán số đại số [ sửa ] Số nguyên [ sửa ]
Cộng trừ nhân chia số nguyên với số không
a
+
0
=
a
{\displaystyle a+0=a}
a
−
0
=
a
{\displaystyle a-0=a}
a
×
0
=
0
{\displaystyle a\times 0=0}
a
/
0
=
o
o
{\displaystyle a/0=oo}
a
+
(
−
a
)
=
0
{\displaystyle a+(-a)=0}
a
−
(
−
a
)
=
2
a
{\displaystyle a-(-a)=2a}
a
×
(
−
a
)
=
−
a
2
{\displaystyle a\times (-a)=-a^{2}}
a
/
(
−
a
)
=
−
1
{\displaystyle a/(-a)=-1}
a
+
a
=
2
a
{\displaystyle a+a=2a}
a
−
a
=
0
{\displaystyle a-a=0}
a
×
a
=
a
2
{\displaystyle a\times a=a^{2}}
a
a
=
1
{\displaystyle {\frac {a}{a}}=1}
a
0
=
1
{\displaystyle a^{0}=1}
a
n
=
a
×
a
×
a
.
.
.
×
a
{\displaystyle a^{n}=a\times a\times a...\times a}
(
−
a
)
n
=
a
n
{\displaystyle (-a)^{n}=a^{n}}
n
=
2
m
{\displaystyle n=2m}
(
−
a
)
n
=
−
a
n
{\displaystyle (-a)^{n}=-a^{n}}
n
=
2
m
+
1
{\displaystyle n=2m+1}
0
=
0
{\displaystyle {\sqrt {0}}=0}
1
=
1
{\displaystyle {\sqrt {1}}=1}
(
−
1
)
=
j
{\displaystyle {\sqrt {(-1)}}=j}
Lũy thừa [ sửa ] Toán căn [ sửa ] Toán log [ sửa ]
Toán Log
L
o
g
a
b
=
c
{\displaystyle Log_{a}b=c}
a
c
=
b
{\displaystyle a^{c}=b}
Viết tắc
L
o
g
=
L
o
g
10
{\displaystyle Log=Log_{10}}
L
n
=
L
o
g
2
{\displaystyle Ln=Log_{2}}
Log 1
L
o
g
(
1
)
=
0
{\displaystyle Log(1)=0}
Log lũy thừa
L
o
g
n
(
A
)
n
=
A
{\displaystyle Log_{n}(A)^{n}=A}
Lũy thừa log
B
L
o
g
B
(
A
)
=
A
{\displaystyle B^{Log_{B}(A)}=A}
Log của tích số
L
o
g
(
A
B
)
=
L
o
g
A
+
L
o
g
B
{\displaystyle Log(AB)=LogA+LogB}
Log của thương số
L
o
g
(
A
B
)
=
L
o
g
A
−
L
o
g
B
{\displaystyle Log({\frac {A}{B}})=LogA-LogB}
Log của lủy thừa
L
o
g
(
A
n
)
=
n
L
o
g
A
{\displaystyle Log(A^{n})=nLogA}
Đổi nền log
L
o
g
a
x
=
L
o
g
x
L
o
g
a
{\displaystyle Log_{a}x={\frac {Logx}{Loga}}}
Toán số phức [ sửa ] Số phức được biểu diển như ở dưới đây
Số phức Thuận
Z
{\displaystyle Z}
Nghịch
Z
∗
{\displaystyle Z^{*}}
Biểu diển dưới dạng xy
Z
=
x
+
j
y
{\displaystyle Z=x+jy}
Z
=
x
−
j
y
{\displaystyle Z=x-jy}
Biểu diển dưới dạng Zθ
Z
∠
θ
=
x
2
+
y
2
∠
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle tan^{-1}{\frac {y}{x}}}
Z
∠
θ
=
x
2
+
y
2
∠
−
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {x^{2}+y^{2}}}\angle -tan^{-1}{\frac {y}{x}}}
Biểu diển dưới dạng hàm số lượng giác
Z
=
z
(
c
o
s
θ
+
j
s
i
n
θ
)
{\displaystyle Z=z(cos\theta +jsin\theta )}
Z
=
z
(
c
o
s
θ
−
j
s
i
n
θ
)
{\displaystyle Z=z(cos\theta -jsin\theta )}
Biểu diển dưới lũy thừa của e
Z
=
z
e
j
θ
{\displaystyle Z=ze^{j\theta }}
Z
=
z
e
−
j
θ
{\displaystyle Z=ze^{-j\theta }}
Toán số phức được thực thi như sau
Toán Số phức Toán cộng Toán trừ Toán nhân Toán chia
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
x
+
j
y
{\displaystyle x+jy}
x
−
j
y
{\displaystyle x-jy}
2
x
{\displaystyle 2x}
2
y
{\displaystyle 2y}
x
2
−
y
2
{\displaystyle x^{2}-y^{2}}
x
2
−
y
2
x
−
j
y
{\displaystyle {\frac {x^{2}-y^{2}}{x-jy}}}
Z
=
z
e
j
θ
{\displaystyle Z=ze^{j\theta }}
Z
=
z
e
−
j
θ
{\displaystyle Z=ze^{-j\theta }}
z
(
e
j
θ
+
e
−
j
θ
)
{\displaystyle z(e^{j\theta }+e^{-j\theta })}
z
(
e
j
θ
−
e
−
j
θ
)
{\displaystyle z(e^{j\theta }-e^{-j\theta })}
z
2
{\displaystyle z^{2}}
e
j
2
θ
{\displaystyle e^{j2\theta }}
Định lý Demoive
(
Z
∠
θ
)
n
=
Z
n
∠
n
θ
{\displaystyle (Z\angle \theta )^{n}=Z^{n}\angle n\theta }
Dải số [ sửa ] Dải số [ sửa ] Dải số là một dải số có định dạng . Thí dụ
Dải số của các số tự nhiên
1
,
2
,
3
,
4
,
5
,
.
.
.
.
,
n
{\displaystyle 1,2,3,4,5,....,n}
Dải số của các số tự nhiên chẳn
1
,
2
,
4
,
6
,
8
,
10
,
.
.
.
,
2
n
{\displaystyle 1,2,4,6,8,10,...,2n}
Tổng chuổi số [ sửa ] Tổng số một phép toán giải tích tìm tổng của một dải số như sau
s
=
1
+
2
+
3
+
.
.
.
+
n
=
k
(
1
+
n
)
{\displaystyle s=1+2+3+...+n=k(1+n)}
Tổng dải số có ký hiệu
∑
{\displaystyle \sum }
Tổng của dải số từ 1 đến n có thể viết như sau
S
n
=
∑
i
=
1
n
a
i
=
1
+
2
+
⋯
+
n
{\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}=1+2+\cdots +n}
.
Tổng chuổi số cấp số cộng [ sửa ] Dạng tổng quát
Tổng chuổi số cấp số cộng có dạng tổng quát
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}
Chứng minh
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
n
2
(
2
a
+
(
n
−
1
)
d
)
{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}
S
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}
S
=
[
a
+
(
n
−
1
)
d
]
+
.
.
.
+
(
n
−
1
)
d
]
+
a
{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}
2
S
=
[
2
a
+
(
n
−
1
)
d
]
n
{\displaystyle 2S=[2a+(n-1)d]n}
S
=
[
2
a
+
(
n
−
1
)
d
]
n
2
{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}
Thí dụ
Dải số cấp số cộng có dạng tổng quát
1
,
2
,
3
,
.
.
.9
{\displaystyle 1,2,3,...9}
Tổng số của dải số
1
+
2
+
3
+
4
+
5
+
.
.
.9
=
50
{\displaystyle 1+2+3+4+5+...9=50}
Cách giải
S
=
(
1
+
9
)
+
(
2
+
8
)
+
(
3
+
7
)
+
(
4
+
6
)
+
(
5
+
5
)
=
10
(
5
)
=
50
{\displaystyle S=(1+9)+(2+8)+(3+7)+(4+6)+(5+5)=10(5)=50}
Tổng chuổi số cấp số nhân [ sửa ] Dạng tổng quát
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
∑
k
=
0
∞
(
a
r
k
)
{\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}=\sum _{k=0}^{\infty }(ar^{k})}
Chứng minh
∑
k
=
0
∞
(
a
r
k
)
=
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle \sum _{k=0}^{\infty }(ar^{k})=a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}={\frac {a(1-r^{n})}{1-r}}}
S
=
a
+
a
r
+
a
r
2
+
a
r
3
+
.
.
.
+
a
r
n
−
1
{\displaystyle S=a+ar+ar^{2}+ar^{3}+...+ar^{n-1}}
r
S
=
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
.
.
.
+
a
r
n
{\displaystyle rS=ar+ar^{2}+ar^{3}+ar^{4}+...+ar^{n}}
S
−
r
S
=
a
−
a
r
n
{\displaystyle S-rS=a-ar^{n}}
S
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle S={\frac {a(1-r^{n})}{1-r}}}
S
=
a
1
−
r
{\displaystyle S={\frac {a}{1-r}}}
n
<
1
{\displaystyle n<1}
Thí dụ
1
+
1.1
+
1.1
2
+
1.1
3
=
4
{\displaystyle 1+1.1+1.1^{2}+1.1^{3}=4}
1
+
1.2
+
1.2
2
+
1.2
3
=
1
+
2
+
4
+
8
=
15
{\displaystyle 1+1.2+1.2^{2}+1.2^{3}=1+2+4+8=15}
Tổng chuổi số Pascal [ sửa ] Công thức tổng quát lũy thừa n của một tổng
(
x
+
y
)
n
=
∑
r
=
0
n
(
n
r
)
x
r
y
n
−
r
{\displaystyle (x+y)^{n}=\sum _{r=0}^{n}{n \choose r}x^{r}y^{n-r}}
(
x
+
y
)
n
=
(
n
0
)
x
0
y
n
+
(
n
1
)
x
1
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
(
n
n
−
1
)
x
n
−
1
y
1
+
(
n
n
)
x
n
y
0
{\displaystyle (x+y)^{n}={n \choose 0}x^{0}y^{n}+{n \choose 1}x^{1}y^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+{n \choose {n-1}}x^{n-1}y^{1}+{n \choose n}x^{n}y^{0}}
(
x
+
y
)
n
=
y
n
+
n
x
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
n
x
n
−
1
y
+
x
n
{\displaystyle (x+y)^{n}=y^{n}+nxy^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+nx^{n-1}y+x^{n}}
Với
(
n
r
)
=
n
!
r
!
(
n
−
r
)
!
{\displaystyle {n \choose r}={\frac {n!}{r!(n-r)!}}}
Thí dụ
(
x
+
1
)
1
=
{\displaystyle (x+1)^{1}=}
1
x
+
1
{\displaystyle 1x+1}
(
x
+
1
)
2
=
{\displaystyle (x+1)^{2}=}
1
x
2
+
2
x
+
1
{\displaystyle 1x^{2}+2x+1}
(
x
+
1
)
3
=
{\displaystyle (x+1)^{3}=}
1
x
3
+
3
x
2
+
3
x
+
1
{\displaystyle 1x^{3}+3x^{2}+3x+1}
(
x
+
1
)
4
=
{\displaystyle (x+1)^{4}=}
1
x
4
+
4
x
3
+
6
x
2
+
4
x
+
1
{\displaystyle 1x^{4}+4x^{3}+6x^{2}+4x+1}
(
x
+
1
)
5
=
{\displaystyle (x+1)^{5}=}
1
x
5
+
5
x
4
+
10
x
3
+
10
x
2
+
5
x
+
1
{\displaystyle 1x^{5}+5x^{4}+10x^{3}+10x^{2}+5x+1}
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
Tổng chuổi số Taylor [ sửa ] Dạng tổng quá
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
f
‴
(
a
)
3
!
(
x
−
a
)
3
+
⋯
=
∑
n
=
0
∞
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}
Tổng dải số Maclaurin [ sửa ] Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
+
.
.
.
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
+
.
.
.
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}+...=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}+...}
Chứng minh
Khi x=0
f
(
0
)
=
a
0
{\displaystyle f(0)=a_{0}}
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
f
′
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
4
a
4
x
3
{\displaystyle f^{'}(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+4a_{4}x^{3}}
f
′
(
0
)
=
a
1
{\displaystyle f^{'}(0)=a_{1}}
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
f
″
(
x
)
=
2
a
2
+
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
a
4
x
2
+
(
5
)
(
4
)
a
5
x
3
{\displaystyle f^{''}(x)=2a_{2}+(3)(2)a_{3}x+(4)(3)a_{4}x^{2}+(5)(4)a_{5}x^{3}}
f
″
(
0
)
=
2
a
2
{\displaystyle f^{''}(0)=2a_{2}}
a
2
=
f
″
(
0
)
2
{\displaystyle a_{2}={\frac {f^{''}(0)}{2}}}
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
f
‴
(
x
)
=
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
(
2
)
a
4
x
+
(
5
)
(
4
)
(
3
)
a
5
x
2
{\displaystyle f^{'''}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_{5}x^{2}}
f
‴
(
0
)
=
(
3
)
(
2
)
a
3
{\displaystyle f^{'''}(0)=(3)(2)a_{3}}
a
3
=
f
‴
(
0
)
3
!
{\displaystyle a_{3}={\frac {f^{'''}(0)}{3!}}}
Thế
a
0
,
a
−
1
,
a
−
2
{\displaystyle a_{0},a-1,a-2}
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}}
f
(
x
)
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
{\displaystyle f(x)=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}}
Thí dụ=
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f(0)=\sin(0)=0}
f
″
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{''}(x)=-\sin(x)}
f
″
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{''}(0)=-\sin(0)=0}
f
‴
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{'''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
sin
(
x
)
=
0
+
x
(
1
)
+
x
2
2
!
(
0
)
+
x
3
3
!
(
−
1
)
+
x
5
5
!
(
1
)
=
x
−
x
3
3
!
+
x
5
5
!
{\displaystyle \sin(x)=0+x(1)+{\frac {x^{2}}{2!}}(0)+{\frac {x^{3}}{3!}}(-1)+{\frac {x^{5}}{5!}}(1)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
0
)
=
cos
(
0
)
=
1
{\displaystyle f(0)=\cos(0)=1}
f
′
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{'}(x)=-\sin(x)}
f
′
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{'}(0)=-\sin(0)=0}
f
″
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
f
‴
(
x
)
=
sin
(
x
)
{\displaystyle f^{'''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
cos
(
x
)
=
1
+
x
(
0
)
+
x
2
2
!
(
−
1
)
+
x
3
3
!
(
0
)
+
x
4
4
!
(
1
)
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
{\displaystyle \cos(x)=1+x(0)+{\frac {x^{2}}{2!}}(-1)+{\frac {x^{3}}{3!}}(0)+{\frac {x^{4}}{4!}}(1)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}}
Tổng chuổi số Fourier [ sửa ] Tổng chuổi số Fourier đại diện cho tổng chuổi số hàm số sóng sine
s
N
(
x
)
=
A
0
2
+
∑
n
=
1
N
A
n
⋅
sin
(
2
π
n
x
P
+
ϕ
n
)
,
for integer
N
≥
1.
{\displaystyle s_{N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}A_{n}\cdot \sin \left({\tfrac {2\pi nx}{P}}+\phi _{n}\right),\quad {\text{for integer}}\ N\ \geq \ 1.}
Công thức tổng dải số [ sửa ]
∑
k
=
0
n
c
=
n
c
{\displaystyle \sum _{k=0}^{n}{c}=nc}
c
{\displaystyle c}
∑
k
=
0
n
k
=
n
(
n
+
1
)
2
{\displaystyle \sum _{k=0}^{n}{k}={\frac {n(n+1)}{2}}}
∑
k
=
0
n
k
2
=
n
(
n
+
1
)
(
2
n
+
1
)
6
{\displaystyle \sum _{k=0}^{n}{k^{2}}={\frac {n(n+1)(2n+1)}{6}}}
∑
k
=
0
n
k
3
=
n
2
(
n
+
1
)
2
4
{\displaystyle \sum _{k=0}^{n}{k^{3}}={\frac {n^{2}(n+1)^{2}}{4}}}
∑
n
=
0
∞
x
n
n
!
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
x
4
4
!
+
⋯
=
e
x
{\displaystyle \sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots =e^{x}}
∑
n
=
1
∞
(
−
1
)
n
+
1
n
x
n
=
x
−
x
2
2
+
x
3
3
−
x
4
4
+
⋯
=
ln
(
1
+
x
)
for
|
x
|
<
1
{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\cdots =\ln(1+x)\quad {\text{ for }}|x|<1}
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
x
2
n
=
1
−
x
2
2
!
+
x
4
4
!
−
⋯
=
cos
(
x
)
for all
x
∈
C
{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots =\cos(x)\quad {\text{ for all }}x\in \mathbb {C} }
Biểu thức [ sửa ] Một đa thức đại số của nhiều đơn thức đại số
Thí dụ
2
x
+
5
y
−
3
{\displaystyle 2x+5y-3}
Phép toán biểu thức [ sửa ] Thứ tự thực thi phép toán biểu thức đại số như sau
Thí dụ
A
=
2
x
+
5
y
−
3
{\displaystyle A=2x+5y-3}
B
=
52
y
−
5
{\displaystyle B=52y-5}
A
+
B
=
(
2
x
+
5
y
−
3
)
+
(
52
y
−
5
)
=
2
x
+
(
5
y
+
52
y
)
+
(
−
3
−
5
)
=
2
x
+
57
y
−
8
{\displaystyle A+B=(2x+5y-3)+(52y-5)=2x+(5y+52y)+(-3-5)=2x+57y-8}
A
−
B
=
(
2
x
+
5
y
−
3
)
−
(
52
y
−
5
)
=
2
x
+
(
5
y
−
52
y
)
+
[
−
3
−
(
−
5
)
]
=
2
x
−
47
y
+
2
{\displaystyle A-B=(2x+5y-3)-(52y-5)=2x+(5y-52y)+[-3-(-5)]=2x-47y+2}
Đẳng thức [ sửa ] Định nghỉa [ sửa ] Đẳng thức đại diện cho 2 đa thức bằng nhau . Thí dụ như Định lý Pythagore về tương quan các cạnh trong tam giác vuông
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}}
Các đẳng thức đạo số cơ bản [ sửa ] Bình phương tổng 2 số đại số
(
a
+
b
)
2
=
(
a
+
b
)
(
a
+
b
)
=
a
2
+
a
b
+
a
b
+
b
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=(a+b)(a+b)=a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}}
Bình phương hiệu 2 số đại số
(
a
−
b
)
2
=
(
a
−
b
)
(
a
−
b
)
=
a
2
−
a
b
−
a
b
+
b
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=(a-b)(a-b)=a^{2}-ab-ab+b^{2}=a^{2}-2ab+b^{2}}
Tổng 2 bình phương
a
2
+
b
2
=
(
a
+
b
)
2
−
2
a
b
{\displaystyle a^{2}+b^{2}=(a+b)^{2}-2ab}
a
2
+
b
2
=
(
a
−
b
)
2
+
2
a
b
{\displaystyle a^{2}+b^{2}=(a-b)^{2}+2ab}
Hiệu 2 bình phương
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
Tổng 2 lập phương
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})}
Hiệu 2 lập phương
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}
Bất đẳng thức [ sửa ] Định nghỉa [ sửa ] Bất đẳng thức đại diện cho 2 đa thức không bằng nhau
a
+
b
{\displaystyle a+b}
a
+
b
{\displaystyle a+b}
Hàm số [ sửa ] Tính chất [ sửa ]
Hàm số Công thức
Hàm số có dạng tổng quát
f
(
x
,
y
,
z
,
.
.
.
)
{\displaystyle f(x,y,z,...)}
Giá trị hàm số
f
(
x
,
y
,
z
,
.
.
.
)
=
C
{\displaystyle f(x,y,z,...)=C}
Loại hàm số [ sửa ]
Dạng hàm số Công thức Thí dụ
Hàm số tuần hoàn Periodic function
f
(
t
)
=
f
(
t
+
T
)
{\displaystyle f(t)=f(t+T)}
s
i
n
x
=
s
i
n
(
x
+
k
2
π
)
{\displaystyle sinx=sin(x+k2\pi )}
Hàm số chẳn even function
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
Hàm số lẽ odd function
f
(
x
)
=
−
f
(
x
)
{\displaystyle f(x)=-f(x)}
y
(
x
)
=
−
y
(
x
)
{\displaystyle y(x)=-y(x)}
Hàm số nghịch đảo inverse function
f
−
1
(
x
)
=
1
f
(
x
)
{\displaystyle f^{-1}(x)={\frac {1}{f(x)}}}
s
i
n
−
1
x
=
1
s
i
n
x
{\displaystyle sin^{-1}{x}={\frac {1}{sinx}}}
Hàm số trong hàm số composite function
f
(
x
)
=
f
(
g
(
x
)
)
{\displaystyle f(x)=f(g(x))}
Hàm số nhiều biến số parametric function
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Hàm số tương quan/]] recursive function
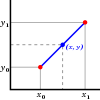
Phép toán hàm số [ sửa ] Đồ thị hàm số [ sửa ] Với mọi giá trị của x sẻ có một giá trị hàm số của x tương đương . Thí dụ, với hàm số f(x)=x ta có thể thiết lập bảng giá trị tương quan của x và hàm số của x . Khi đặt các giá trị của x và của f(x) trên đồ thị XY ta có thể vẻ được hình đường thẳng có độ góc bằng 1 đi qua điểm gốc ở tọa độ (0,0)
x -2
-1
0
1
2
Hình
F(x)=x -2
-1
0
1
2
x
Công thức toán hàm số [ sửa ] Biểu diển hàm số bằng tổng dải số Maclaurin [ sửa ] Toán hàm số [ sửa ] Với mọi hàm số
y
=
f
(
x
)
{\displaystyle y=f(x)}
Thay đổi biến số
Δ
x
=
(
x
+
Δ
x
)
−
x
{\displaystyle \Delta x=(x+\Delta x)-x}
Δ
y
=
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=\Delta f(x)=f(x+\Delta x)-f(x)}
Tỉ lệ thay đổi biến số
Δ
y
Δ
x
=
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}}
Giới hạn
lim
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
=
f
(
Δ
x
)
−
f
(
0
)
(
Δ
x
)
{\displaystyle \lim _{x\to 0}{\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}={\frac {f(\Delta x)-f(0)}{(\Delta x)}}}
Đạo hàm
d
d
x
f
(
x
)
=
f
′
(
x
)
=
lim
Δ
x
→
0
∑
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
∑
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=f^{'}(x)=\lim _{\Delta x\to 0}\sum {\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}\sum {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
Tích phân Tích phân bất định
∫
f
(
x
)
d
x
=
lim
Δ
x
→
0
∑
(
f
(
x
)
+
Δ
f
(
x
)
2
)
Δ
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)dx=\lim _{\Delta x\rightarrow 0}\sum (f(x)+{\frac {\Delta f(x)}{2}})\Delta x=F(x)+C}
Tích phân xác định
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)}
Phương trình [ sửa ] Dạng tổng quát [ sửa ] Phương trình có dạng tổng quát
f
(
x
,
y
,
z
,
.
.
.
)
=
0
{\displaystyle f(x,y,z,...)=0}
Loại phương trình [ sửa ]
Phương trình lũy thừa Dạng tổng quát
Phương trình lũy thừa bậc n
a
n
x
n
+
a
n
−
1
x
n
−
1
+
.
.
.
+
a
1
x
+
a
o
=
0
{\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{o}=0}
Phương trình lũy thừa đạo hàm bậc n
a
n
f
n
(
x
)
+
a
n
−
1
f
n
−
1
(
x
)
+
.
.
.
+
a
o
f
0
(
x
)
=
0
{\displaystyle a_{n}f^{n}(x)+a_{n-1}f^{n-1}(x)+...+a_{o}f^{0}(x)=0}
Hệ phương trình
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
d
x
+
e
y
=
f
{\displaystyle dx+ey=f}
Giải phương trình [ sửa ] Giải phương trình lũy thừa [ sửa ] Giải phương trình đạo hàm [ sửa ] 
![{\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83064172516d2185efbd65172ed7cc9d3e701284)
![{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ddb7d13541806e35a6053ba614df98a87b655)
![{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c5b6f1d86ff3f156fd65ff5857f5e95f89c10e)
![{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2a5db1feeaf9814ba2e7c2618c255f45f299a8)
![{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63777c0be192f9fe36871fbf7d21970aaed89899)
![{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c376b47de6ed1cfc662cad50bbc979688886f30)
![{\displaystyle 2S=[2a+(n-1)d]n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f47f5f57718103fa0610bc7149959105b3a09039)
![{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/220eac7734e9963f251e2cac7519edcaf6af5420)
![{\displaystyle A-B=(2x+5y-3)-(52y-5)=2x+(5y-52y)+[-3-(-5)]=2x-47y+2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b408c9cc2f522c6b7708d057b56b8972389ed9)
