Sách công thức/Sách công thức Điện từ

Nam châm

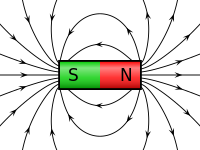
Nam châm là một vật liệu hoặc vật thể tạo ra từ trường. Từ trường này vô hình và có khả năng tạo ra lực từ hút các vật liệu sắt nằm kề bên nam châm .

Tính chất

Mọi Nam châm đều có 2 cực , Cực bắc và Cực nam . Từ trường tạo ra từ các đường sức lực (Lực từ) đi từ cực bắc đến cực nam . Khả năng hút vật liệu từ như Sắt, Nam châm khác về hướng mình

Loại nam châm

Nam châm thừong

Nam châm điện

Nam châm điện	Hình	Công thức
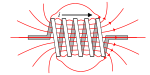
Nam châm điện Từ trường của cộng dây thẳng dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {2\pi r}{l}}I$
Nam châm điện Từ trường của vòng tròn dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {2\pi }{l}}I$
Nam châm điện Từ trường của N vòng tròn dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {N\mu }{l}}I$
Nam châm điện vỉnh cửu		$B=LI={\frac {N\mu }{l}}I$ $H={\frac {B}{\mu }}={\frac {NI}{l}}$

Điện từ trường

Định luật Điện từ trường

Các Định luật điện từ được phát triển bởi nhiều nhà khoa học gia

Định luật Điện từ trường	Ý nghỉa	Công thức
Định luật Coulomb	Lực hút 2 điện tích	$F_{Q}=K{\frac {Q_{+}Q_{-}}{r^{2}}}$
Định luật Lorentz	Lực điện từ	$F_{EB}=Q(E\pm vB)$
Định luật Gauss	Từ thông	$\Phi _{E}=\oint _{S}\mathbf {E} \cdot d\mathbf {A} ={1 \over \epsilon _{o}}\int _{V}\rho \ dV={\frac {Q_{A}}{\epsilon _{o}}}$ $\Phi _{B}=\oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }$
Định luật Ampere	Từ cảm	$B=Li={\frac {\mu }{A}}i$
Định luật Lentz	Từ cảm ứng	$-\phi =-NB=-NLi$
Định luật Faraday	Điện từ cảm ứng	$-\epsilon =-\int Edl=-{\frac {d\phi _{B}}{dt}}=-NL{\frac {di}{dt}}$
Định luật Maxwell	Từ nhiểm	$H={\frac {B}{\mu }}$
Định luật Maxwell-Ampere	Dòng điện	$i=\oint _{C}\mathbf {H} \cdot \mathrm {d} \mathbf {l} =\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {A} +{\mathrm {d} \over \mathrm {d} t}\iint _{S}\mathbf {D} \cdot \mathrm {d} \mathbf {A}$ $\oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }+{\frac {d\mathbf {\Phi _{E}} }{dt}}$

Cường độ E, B

Cường độ Từ trường B của dẩn điện

Theo Định luật Ampere, cường độ Từ trường được tính như sau

$B={\frac {\mu }{A}}I=LI$

$L={\frac {B}{I}}$

Nam châm điện	Hình	Công thức
Nam châm điện Từ trường của cộng dây thẳng dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {2\pi r}{l}}I$
Nam châm điện Từ trường của vòng tròn dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {2\pi }{l}}I$
Nam châm điện Từ trường của N vòng tròn dẩn điện		$B=LI={\frac {\mu }{A}}I={\frac {N\mu }{l}}I$
Nam châm điện vỉnh cửu		$B=LI={\frac {N\mu }{l}}I$ $H={\frac {B}{\mu }}={\frac {NI}{l}}$

Phương trình Maxwell

Phương trình điện từ nhiểm

Tên	Dạng phương trình vi phân	Dạng tích phân
Định luật Gauss:	$\nabla \cdot \mathbf {D} =\rho$	$\oint _{S}\mathbf {D} \cdot d\mathbf {A} =\int _{V}\rho dV$
Đinh luật Gauss cho từ trường (sự không tồn tại của từ tích):	$\nabla \cdot \mathbf {B} =0$	$\oint _{S}\mathbf {B} \cdot d\mathbf {A} =0$
Định luật Faraday cho từ trường:	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	$\oint _{C}\mathbf {E} \cdot d\mathbf {l} =-\ {d \over dt}\int _{S}\mathbf {B} \cdot d\mathbf {A}$
Định luật Ampere (với sự bổ sung của Maxwell):	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$	$\oint _{C}\mathbf {H} \cdot d\mathbf {l} =\int _{S}\mathbf {J} \cdot d\mathbf {A} +{d \over dt}\int _{S}\mathbf {D} \cdot d\mathbf {A}$

Phương trình vector dao động điện từ

Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T}}B$
$T=\mu \epsilon$

Sóng điện từ

Dao động điện từ

Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T}}B$
$T=\mu \epsilon$

Dùng phép toán

$\nabla (\nabla \times E)=\nabla (-{\frac {1}{T}}E)=\nabla ^{2}E$

$\nabla (\nabla \times B)=\nabla (-{\frac {1}{T}}B)=\nabla ^{2}B$

Phương trình sóng điện từ

Cho một Phương trình sóng điện từ

$\nabla ^{2}E=-\omega E$

$\nabla ^{2}B=-\omega B$

$\omega ={\sqrt {\frac {1}{T}}}$

Hàm số sóng điện từ

Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ

$E=ASin\omega t$

$B=ASin\omega t$

$\omega =\lambda f={\sqrt {\frac {1}{T}}}=C$

$T=\mu \epsilon$

Chuyển động sóng điện từ

$v=\omega =\lambda f={\sqrt {\frac {1}{\mu \epsilon }}}=C$

$W=pv=pC=p\lambda f=hf$

Với

$h=p\lambda$

Lượng tử

Một đại lượng không có khối lượng và có giá trị là một hằng số không đổi

$h=p\lambda$

Lượng tử có lưởng tính Sóng Hạt . Lưởng tính Sóng - Hạt cho phép lượng tử di chuyển dưới dạng Sóng điện từ và truyền năng lượng dưới dạng Hạt

$\lambda ={\frac {h}{p}}$ . Đặc tính Sóng

$p={\frac {h}{\lambda }}$. Đặc tính Hạt

Có 2 loại lượng được tìm thấy là Lượng tử quang ở $f=f_{o}$ và Lượng tử điện ở $f>f_{o}$

$h=p\lambda _{o}=p{\frac {C}{f_{o}}}$ . Lượng tử quang

$h=p\lambda =p{\frac {C}{f}}$ . Lượng tử điện

Năng lực lượng tử nhiệt điện từ

Mọi lượng tử đều có một năng lực lượng tử tính bằng

$W=hf=h{\frac {C}{\lambda }}$

Năng lực lượng tử được tìm thấy ở 2 trạng thái Năng lực lượng tử quang ở $f=f_{o}$và Năng lực lượng tử điện ở $f>f_{o}$

Năng lực lượng tử quang

$W_{o}=hf_{o}=h{\frac {C}{\lambda _{o}}}$

Năng lực lượng tử điện

$W=hf=h{\frac {C}{\lambda }}$

Xác xuất tìm thấy Năng lực lượng tử của lượng tử được phát biểu trong Định luật Heinseinberg

Năng lực lượng tử chỉ có thể tìm thấy ở 1 trong 2 trạng thái Năng lực lượng tử quang hay Năng lực lượng tử điện

Có thể biểu diển bằng công thức toán

${\frac {1}{2}}h$

Phổ tần Phóng xạ sóng điện từ

Phóng xạ sóng điện từ có phổ tần phóng xạ sau

VF , Ánh sáng thấy được

UVF , Ánh sáng tím

X, Tia X

γ, Tia gamma