[ sửa ] Các định luật về Chuyển động của Newton là một hệ thống gồm 3 định luật đặt nền móng cơ bản cho cơ học cổ điển. Chúng mô tả mối quan hệ giữa một vật thể và các lực tác động cũng như chuyển động của vật thể đó. Các định luật đã được diễn giải theo nhiều cách khác nhau trong suốt 3 thế kỷ sau đó.
F = 0
Không có lực tương tác , không có chuyển động
Vật sẽ đứng yên
F≠ 0
Lực tương tác với vật tạo ra chuyển động
Vật sẽ di chuyển
Σ F = 0
Tổng lực trên vật bằng không, vật ở trạng thái cân bằng
Vật ở trạng thái cân bằng
[ sửa ] [ sửa ] O →
F
=
m
v
t
=
p
t
{\displaystyle F=m{\frac {v}{t}}={\frac {p}{t}}}
p
=
m
v
=
F
t
{\displaystyle p=mv=Ft}
[ sửa ] O
↓
F
g
=
m
g
=
m
M
G
h
2
{\displaystyle F_{g}=mg={\frac {mMG}{h^{2}}}}
h
=
m
M
G
F
{\displaystyle h={\sqrt {\frac {mMG}{F}}}}
[ sửa ] ↑
O
↓
F
p
=
F
g
{\displaystyle F_{p}=F_{g}}
m
v
t
=
m
g
{\displaystyle {\frac {mv}{t}}=mg}
a
=
g
=
M
G
h
2
{\displaystyle a=g={\frac {MG}{h^{2}}}}
h
=
M
G
a
{\displaystyle h={\sqrt {\frac {MG}{a}}}}
v
=
g
t
{\displaystyle v=gt}
t
=
v
g
{\displaystyle t={\frac {v}{g}}}
W
p
=
W
g
{\displaystyle W_{p}=W_{g}}
m
v
2
2
=
m
g
h
{\displaystyle {\frac {mv^{2}}{2}}=mgh}
v
=
2
g
h
{\displaystyle v={\sqrt {2gh}}}
d
=
v
2
2
g
{\displaystyle d={\frac {v^{2}}{2g}}}
[ sửa ]
F
→
=
F
→
p
+
F
→
g
=
F
p
i
→
+
F
g
j
→
{\displaystyle {\vec {F}}={\vec {F}}_{p}+{\vec {F}}_{g}=F_{p}{\vec {i}}+F_{g}{\vec {j}}}
[ sửa ]
F
r
=
F
g
{\displaystyle F_{r}=F_{g}}
m
v
r
=
m
g
{\displaystyle mvr=mg}
v
=
g
r
{\displaystyle v={\frac {g}{r}}}
r
=
g
v
{\displaystyle r={\frac {g}{v}}}
W
r
=
W
g
{\displaystyle W_{r}=W_{g}}
m
v
2
r
=
m
g
h
{\displaystyle {\frac {mv^{2}}{r}}=mgh}
v
=
r
g
h
{\displaystyle v={\sqrt {rgh}}}
h
=
v
2
r
g
{\displaystyle h={\frac {v^{2}}{rg}}}
[ sửa ] [ sửa ]
F
μ
=
F
p
{\displaystyle F_{\mu }=F_{p}}
μ
F
N
=
m
v
t
{\displaystyle \mu F_{N}=m{\frac {v}{t}}}
v
=
μ
F
N
t
m
{\displaystyle v={\frac {\mu F_{N}t}{m}}}
v
=
m
v
μ
F
N
{\displaystyle v={\frac {mv}{\mu F_{N}}}}
W
μ
=
W
p
{\displaystyle W_{\mu }=W_{p}}
μ
F
N
d
=
m
g
h
{\displaystyle \mu F_{N}d=mgh}
d
=
m
g
h
μ
F
N
{\displaystyle d={\frac {mgh}{\mu F_{N}}}}
h
=
μ
F
N
d
m
g
{\displaystyle h={\frac {\mu F_{N}d}{mg}}}
[ sửa ]
F
→
=
F
→
p
+
F
→
g
=
F
p
i
→
+
F
g
j
→
{\displaystyle {\vec {F}}={\vec {F}}_{p}+{\vec {F}}_{g}=F_{p}{\vec {i}}+F_{g}{\vec {j}}}
F
∠
θ
=
F
p
2
+
F
g
2
∠
T
a
n
−
1
F
g
F
p
{\displaystyle F\angle \theta ={\sqrt {F_{p}^{2}+F_{g}^{2}}}\angle Tan^{-1}{\frac {F_{g}}{F_{p}}}}
F
p
=
m
v
t
=
p
t
{\displaystyle F_{p}=m{\frac {v}{t}}={\frac {p}{t}}}
F
g
=
m
g
{\displaystyle F_{g}=mg}
θ
=
∠
T
a
n
−
1
F
g
F
p
=
g
t
v
{\displaystyle \theta =\angle Tan^{-1}{\frac {F_{g}}{F_{p}}}={\frac {gt}{v}}}
[ sửa ] Lực hút giửa điện tích khác loại
F
=
K
Q
+
Q
−
r
2
{\displaystyle F=K{\frac {Q_{+}Q_{-}}{r^{2}}}}
Khoảng cách giửa 2 điện tích
r
=
K
Q
+
Q
−
F
{\displaystyle r=K{\frac {Q_{+}Q_{-}}{F}}}
Lực điện làm cho điện tích đứng yên di chuyển
F
=
Q
E
{\displaystyle F=QE}
F
=
Q
E
=
Q
V
l
=
W
l
{\displaystyle F=QE=Q{\frac {V}{l}}={\frac {W}{l}}}
l
=
W
F
{\displaystyle l={\frac {W}{F}}}
v
=
l
t
=
W
F
t
=
U
F
{\displaystyle v={\frac {l}{t}}={\frac {W}{Ft}}={\frac {U}{F}}}
t
=
l
v
=
W
F
/
U
F
=
W
F
×
F
U
=
W
U
{\displaystyle t={\frac {l}{v}}={\frac {W}{F}}/{\frac {U}{F}}={\frac {W}{F}}\times {\frac {F}{U}}={\frac {W}{U}}}
Lực điện làm cho điện tích di chuyển theo hướng dọc
F
=
±
Q
v
B
{\displaystyle F=\pm QvB}
F
=
Q
v
B
=
I
t
v
B
=
I
l
B
{\displaystyle F=QvB=ItvB=IlB}
l
=
F
I
B
{\displaystyle l={\frac {F}{IB}}}
v
=
F
Q
v
{\displaystyle v={\frac {F}{Qv}}}
t
=
l
v
=
F
I
B
/
F
Q
v
=
F
I
B
×
Q
v
F
=
Q
v
I
B
{\displaystyle t={\frac {l}{v}}={\frac {F}{IB}}/{\frac {F}{Qv}}={\frac {F}{IB}}\times {\frac {Qv}{F}}={\frac {Qv}{IB}}}
Lực điện làm cho điện tích di chuyển theo hướng nghiêng
F
=
Q
(
E
±
v
B
)
{\displaystyle F=Q(E\pm vB)}
Khi
v
=
0
{\displaystyle v=0}
F
=
Q
(
E
±
v
B
)
=
Q
E
{\displaystyle F=Q(E\pm vB)=QE}
Khi v ≠ 0 ,
Q
E
=
0
{\displaystyle QE=0}
F
=
Q
(
E
±
v
B
)
=
Q
v
B
{\displaystyle F=Q(E\pm vB)=QvB}
Khi
E
±
v
B
=
0
{\displaystyle E\pm vB=0}
F
=
Q
(
E
±
v
B
)
=
0
{\displaystyle F=Q(E\pm vB)=0}
E
=
v
B
{\displaystyle E=vB}
B
=
1
v
B
{\displaystyle B={\frac {1}{v}}B}
v
=
E
B
{\displaystyle v={\frac {E}{B}}}
Đừong dài đường thẳng nghiêng
l
=
l
E
2
+
l
B
2
=
(
Q
v
F
)
2
+
(
F
I
B
)
2
{\displaystyle l={\sqrt {l_{E}^{2}+l_{B}^{2}}}={\sqrt {({\frac {Qv}{F}})^{2}+({\frac {F}{IB}})^{2}}}}
Tổng lực làm cho điện tích di chuyển theo vòng tròn
F
p
=
F
B
{\displaystyle F_{p}=F_{B}}
m
v
2
r
=
Q
v
B
{\displaystyle m{\frac {v^{2}}{r}}=QvB}
Q
m
=
v
2
r
v
B
=
v
r
B
{\displaystyle {\frac {Q}{m}}={\frac {v^{2}}{rvB}}={\frac {v}{rB}}}
r
=
m
v
2
Q
B
{\displaystyle r={\frac {mv^{2}}{QB}}}
[ sửa ]
F
=
k
Q
+
Q
−
r
2
=
k
Z
e
2
r
2
{\displaystyle F=k{\frac {Q_{+}Q_{-}}{r^{2}}}=k{\frac {Ze^{2}}{r^{2}}}}
Cho lực Coulomb bằng lực ly tâm
k
Z
e
2
r
2
=
m
v
2
r
{\displaystyle k{\frac {Ze^{2}}{r^{2}}}={\frac {mv^{2}}{r}}}
k
Z
e
2
=
m
v
2
r
{\displaystyle kZe^{2}=mv^{2}r}
r
=
k
Z
e
2
m
v
2
{\displaystyle r={\frac {kZe^{2}}{mv^{2}}}}
Bohr điều kiện để lượng tử hóa của góc độn lượng
m
v
r
=
n
h
2
π
{\displaystyle mvr={\frac {nh}{2\pi }}}
Giải tìm v
v
=
n
h
2
π
m
r
{\displaystyle v={\frac {nh}{2\pi mr}}}
Thế v vào r
r
=
k
Z
e
2
m
(
n
h
2
π
m
r
)
2
{\displaystyle r={\frac {kZe^{2}}{m({\frac {nh}{2\pi mr}})^{2}}}}
r
=
k
Z
e
2
m
4
π
2
m
2
r
2
n
2
h
2
{\displaystyle r={\frac {kZe^{2}}{m}}{\frac {4\pi ^{2}m^{2}r^{2}}{n^{2}h^{2}}}}
1
=
4
π
2
k
Z
e
2
m
2
m
n
2
h
2
r
{\displaystyle 1={\frac {4\pi ^{2}kZe^{2}m^{2}}{mn^{2}h^{2}}}r}
r
=
n
2
h
2
4
π
2
k
Z
e
2
m
=
n
2
ℏ
2
m
k
Z
e
2
{\displaystyle r={\frac {n^{2}h^{2}}{4\pi ^{2}kZe^{2}m}}={\frac {n^{2}\hbar ^{2}}{mkZe^{2}}}}
Với Hydrogen Z=1, n=1
r
1
=
0.0529177
n
m
{\displaystyle r_{1}=0.0529177nm}
Bohr radius [ sửa ]
E
=
1
2
m
v
2
−
k
Q
+
Q
−
r
2
{\displaystyle E={\frac {1}{2}}mv^{2}-k{\frac {Q_{+}Q_{-}}{r^{2}}}}
E
=
1
2
m
v
2
−
k
Z
e
2
r
2
{\displaystyle E={\frac {1}{2}}mv^{2}-k{\frac {Ze^{2}}{r^{2}}}}
m
v
2
r
=
k
Z
e
2
r
2
{\displaystyle {\frac {mv^{2}}{r}}=k{\frac {Ze^{2}}{r^{2}}}}
m
v
2
r
r
2
=
k
Z
e
2
r
2
r
2
{\displaystyle {\frac {mv^{2}}{r}}{\frac {r}{2}}=k{\frac {Ze^{2}}{r^{2}}}{\frac {r}{2}}}
1
2
m
v
2
=
k
Z
e
2
2
r
{\displaystyle {\frac {1}{2}}mv^{2}=k{\frac {Ze^{2}}{2r}}}
E
=
k
Z
e
2
2
r
−
k
Z
e
2
r
=
−
k
Z
e
2
2
r
{\displaystyle E=k{\frac {Ze^{2}}{2r}}-k{\frac {Ze^{2}}{r}}=-{\frac {kZe^{2}}{2r}}}
Với Hydrogen Z=1
E
=
−
13.6
e
V
n
2
{\displaystyle E=-{\frac {13.6eV}{n^{2}}}}
n được biết là số lượng tử Principal quantum number
h
f
=
E
3
−
E
2
=
−
13.6
e
V
3
2
−
−
13.6
e
V
2
2
{\displaystyle hf=E_{3}-E_{2}={\frac {-13.6eV}{3^{2}}}-{\frac {-13.6eV}{2^{2}}}}
h
f
=
E
3
−
E
2
=
−
1.511
e
V
+
3.40
e
V
=
1.89
e
V
{\displaystyle hf=E_{3}-E_{2}=-1.511eV+3.40eV=1.89eV}
f
=
1.89
e
V
h
(
1.6
×
10
−
19
e
V
)
=
4.56
×
10
1
4
{\displaystyle f={\frac {1.89eV}{h}}({\frac {1.6\times 10^{-}{19}}{eV}})=4.56\times 10^{1}4}
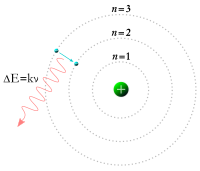
Δ
E
=
E
n
−
E
n
−
1
=
n
h
f
=
n
h
C
λ
{\displaystyle \Delta E=E_{n}-E_{n-1}=nhf=nh{\frac {C}{\lambda }}}
1
λ
=
Δ
E
n
h
C
{\displaystyle {\frac {1}{\lambda }}={\frac {\Delta E}{nhC}}}
Vạch sáng Lyman
1
λ
=
R
(
1
1
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{1^{2}}}-{\frac {1}{n^{2}}})}
Vạch sáng Balmer
1
λ
=
R
(
1
2
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}})}
Vạch sáng Paschen
1
λ
=
R
(
1
3
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{3^{2}}}-{\frac {1}{n^{2}}})}
[ sửa ]
h
f
=
h
f
o
+
1
2
m
v
2
{\displaystyle hf=hf_{o}+{\frac {1}{2}}mv^{2}}
v
=
2
h
Δ
f
m
{\displaystyle v={\sqrt {\frac {2h\Delta f}{m}}}}
h
=
m
v
2
2
Δ
f
{\displaystyle h={\frac {mv^{2}}{2\Delta f}}}
Δ
f
=
f
−
f
o
=
f
−
C
Λ
o
=
f
−
3
×
10
8
m
/
s
400
−
700
n
m
{\displaystyle \Delta f=f-f_{o}=f-{\frac {C}{\Lambda _{o}}}=f-{\frac {3\times 10^{8}m/s}{400-700nm}}}
[ sửa ]
n
h
f
=
m
v
r
(
2
π
)
{\displaystyle nhf=mvr(2\pi )}
v
=
(
1
2
π
)
(
n
h
f
m
r
)
{\displaystyle v=({\frac {1}{2\pi }})({\frac {nhf}{mr}})}
r
=
(
1
2
π
)
(
n
h
f
m
v
)
{\displaystyle r=({\frac {1}{2\pi }})({\frac {nhf}{mv}})}
n
=
2
π
r
(
m
v
h
f
)
{\displaystyle n=2\pi r({\frac {mv}{hf}})}