Sách Vật lý Kỹ sư/Nam châm

Nam châm là một vật liệu hoặc vật thể tạo ra từ trường. Từ trường này vô hình và có khả năng tạo ra lực từ có khả năng hút các vật liệu sắt nằm kề bên nam châm

Tính chất

Mọi Nam châm đều có các đặc tính sau

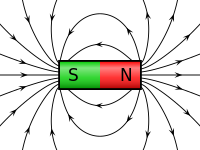
• Mọi nam châm đều có 2 cực , Cực bắc (N) và Cực nam (S) .
• Từ trường tạo ra từ các đường sức lực (Lực từ) đi từ cực bắc đến cực nam .
• Có khả năng hút các kim loại như Sắt
• Có khả năng hút đẩy khi tương tác với Nam châm khác nằm kề bên