Chuyển động được dùng để miêu tả di chuyển của một vật khi có một lực tương tác với vật . Thí dụ như Đá banh đi từ vị trí này sang vị trí khác
[ sửa ] Mọi Chuyển Động từ vị trí ban đầu đến một vị trí khác qua một quãng đường có Đường Dài s trong một Thời Gian t đều có các tính chất sau
Tính Chất Chuyển Động Định nghỉa Ký Hiệu Công Thức Đơn vị
Đường dài đường dài di chuyển
s
{\displaystyle s}
s
{\displaystyle s}
m
Thời gian Thời gian di chuyển
t
{\displaystyle t}
t
{\displaystyle t}
s
Vận tốc Tốc độ di chuyển
v
{\displaystyle v}
s
t
{\displaystyle {\frac {s}{t}}}
m/s
Gia tốc Thay đổi tốc độ theo thay đổi thời gian
a
{\displaystyle a}
v
t
{\displaystyle {\frac {v}{t}}}
m/s2
Lực Sức dùng để thực thi một việc
F
{\displaystyle F}
m
a
=
m
v
t
{\displaystyle ma=m{\frac {v}{t}}}
N
Năng lực khả năng thực thi một việc của lực
W
{\displaystyle W}
F
s
=
F
v
t
{\displaystyle Fs=Fvt}
N m
Năng lượng khả năng thực thi một việc của lực theo thời gian
E
{\displaystyle E}
W
t
=
F
v
{\displaystyle {\frac {W}{t}}=Fv}
N m/s
F
=
m
a
=
m
v
t
=
p
t
{\displaystyle F=ma=m{\frac {v}{t}}={\frac {p}{t}}}
p
=
m
v
=
F
t
{\displaystyle p=mv=Ft}
F
=
p
t
=
h
/
λ
t
=
h
f
λ
{\displaystyle F={\frac {p}{t}}={\frac {h/\lambda }{t}}={\frac {hf}{\lambda }}}
p
=
h
λ
{\displaystyle p={\frac {h}{\lambda }}}
F
=
p
t
β
{\displaystyle F={\frac {p}{t}}\beta }
p
=
F
t
β
=
p
o
γ
{\displaystyle p={\frac {Ft}{\beta }}=p_{o}\gamma }
Mọi chuyển động thẳng di chuyển từ điểm
(
t
o
,
v
o
)
{\displaystyle (t_{o},v_{o})}
(
t
,
v
)
{\displaystyle (t,v)}
a
=
Δ
v
Δ
t
=
v
−
v
o
t
−
t
o
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}}
Vậy, Vận tốc di chuyển
v
=
v
o
+
a
Δ
t
{\displaystyle v=v_{o}+a\Delta t}
v
o
=
v
−
a
Δ
t
{\displaystyle v_{o}=v-a\Delta t}
Δ
t
=
v
−
v
o
a
{\displaystyle \Delta t={\frac {v-v_{o}}{a}}}
Đường dài di chuyển được tính bằng diện tích dưới hình v-t
s
=
v
o
Δ
t
+
Δ
v
2
Δ
t
{\displaystyle s=v_{o}\Delta t+{\frac {\Delta v}{2}}\Delta t}
s
=
Δ
t
(
v
o
+
Δ
v
2
)
{\displaystyle s=\Delta t(v_{o}+{\frac {\Delta v}{2}})}
s
=
Δ
t
(
v
o
+
a
Δ
t
2
)
{\displaystyle s=\Delta t(v_{o}+{\frac {a\Delta t}{2}})}
Δ
v
=
a
Δ
t
{\displaystyle \Delta v=a\Delta t}
s
=
Δ
t
(
v
−
a
Δ
t
2
)
{\displaystyle s=\Delta t(v-{\frac {a\Delta t}{2}})}
v
o
=
v
−
a
Δ
t
{\displaystyle v_{o}=v-a\Delta t}
s
=
(
v
−
v
o
a
)
(
2
v
o
+
v
−
v
o
2
)
=
v
2
−
v
o
2
2
a
{\displaystyle s=({\frac {v-v_{o}}{a}})({\frac {2v_{o}+v-v_{o}}{2}})={\frac {v^{2}-v_{o}^{2}}{2a}}}
Δ
t
=
v
−
v
o
a
{\displaystyle \Delta t={\frac {v-v_{o}}{a}}}
Từ trên
v
2
=
v
o
2
+
2
a
s
{\displaystyle v^{2}=v_{o}^{2}+2as}
[ sửa ]
a
=
Δ
v
Δ
t
=
v
−
v
o
t
−
t
o
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}}
v
=
v
o
+
a
Δ
t
{\displaystyle v=v_{o}+a\Delta t}
s
=
Δ
t
(
v
o
+
Δ
v
2
)
=
Δ
t
(
v
o
+
a
Δ
t
2
)
=
Δ
t
(
v
−
a
Δ
t
2
)
=
v
2
−
v
o
2
2
a
{\displaystyle s=\Delta t(v_{o}+{\frac {\Delta v}{2}})=\Delta t(v_{o}+{\frac {a\Delta t}{2}})=\Delta t(v-{\frac {a\Delta t}{2}})={\frac {v^{2}-v_{o}^{2}}{2a}}}
a
=
Δ
v
Δ
t
=
v
−
v
o
t
−
t
o
=
v
−
0
t
−
0
=
v
t
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}={\frac {v-0}{t-0}}={\frac {v}{t}}}
v
=
a
t
{\displaystyle v=at}
s
=
1
2
v
t
{\displaystyle s={\frac {1}{2}}vt}
[ sửa ]
a
=
Δ
v
Δ
t
=
v
−
v
o
t
−
0
=
Δ
v
t
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-0}}={\frac {\Delta v}{t}}}
v
=
v
o
+
a
t
{\displaystyle v=v_{o}+at}
s
=
t
(
v
o
+
Δ
v
2
)
{\displaystyle s=t(v_{o}+{\frac {\Delta v}{2}})}
a
=
Δ
v
Δ
t
=
v
−
0
t
−
0
=
v
t
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-0}{t-0}}={\frac {v}{t}}}
v
=
a
t
{\displaystyle v=at}
s
=
1
2
v
t
=
1
2
a
t
2
{\displaystyle s={\frac {1}{2}}vt={\frac {1}{2}}at^{2}}
[ sửa ]
a
=
Δ
v
Δ
t
=
v
−
v
o
t
−
t
o
=
0
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}=0}
v
=
v
o
{\displaystyle v=v_{o}}
s
=
v
o
t
{\displaystyle s=v_{o}t}
a
=
−
g
{\displaystyle a=-g}
v
=
−
g
t
{\displaystyle v=-gt}
s
=
−
g
t
2
{\displaystyle s=-gt^{2}}
Với mọi chuyển động cong có vận tốc di chuyển v(t) .
[ sửa ] Gia tốc trung bình của chuyển động được tính như sau
a
=
v
(
t
+
Δ
t
)
−
v
(
t
)
(
t
+
Δ
t
)
−
t
=
Δ
v
(
t
)
Δ
t
{\displaystyle a={\frac {v(t+\Delta t)-v(t)}{(t+\Delta t)-t}}={\frac {\Delta v(t)}{\Delta t}}}
Đường dài trung bình của chuyển động được tính bằng diện tích dưới hình v - t
s
=
Δ
t
[
v
(
t
)
+
Δ
v
(
t
)
2
]
{\displaystyle s=\Delta t[v(t)+{\frac {\Delta v(t)}{2}}]}
[ sửa ] Khi
Δ
t
−
>
0
{\displaystyle \Delta t->0}
Gia tốc tức thời của chuyển động
a
(
t
)
=
lim
Δ
t
→
0
∑
Δ
v
(
t
)
Δ
t
=
d
d
t
v
(
t
)
=
v
′
(
t
)
{\displaystyle a(t)=\lim _{\Delta t\to 0}\sum {\frac {\Delta v(t)}{\Delta t}}={\frac {d}{dt}}v(t)=v^{'}(t)}
Đường dài tức thời của chuyển động
s
(
t
)
=
lim
Δ
t
→
0
∑
(
v
(
t
)
+
Δ
v
(
t
)
2
)
Δ
t
=
∫
v
(
t
)
d
t
=
V
(
t
)
+
C
{\displaystyle s(t)=\lim _{\Delta t\rightarrow 0}\sum (v(t)+{\frac {\Delta v(t)}{2}})\Delta t=\int v(t)dt=V(t)+C}
Cung tròn hướng tâm
α
=
ω
−
ω
o
t
−
t
o
=
Δ
ω
Δ
t
{\displaystyle \alpha ={\frac {\omega -\omega _{o}}{t-t_{o}}}={\frac {\Delta \omega }{\Delta t}}}
ω
=
ω
o
+
α
t
{\displaystyle \omega =\omega _{o}+\alpha t}
θ
=
Δ
t
(
ω
o
+
Δ
ω
2
)
=
Δ
t
(
ω
o
+
α
Δ
t
2
)
=
Δ
t
(
ω
−
α
Δ
t
2
)
=
ω
2
−
ω
o
2
2
α
{\displaystyle \theta =\Delta t(\omega _{o}+{\frac {\Delta \omega }{2}})=\Delta t(\omega _{o}+{\frac {\alpha \Delta t}{2}})=\Delta t(\omega -{\frac {\alpha \Delta t}{2}})={\frac {\omega ^{2}-\omega _{o}^{2}}{2\alpha }}}
Cung tròn ly tâm
Δ
v
v
=
Δ
r
r
=
v
Δ
t
r
=
v
2
r
=
r
ω
2
{\displaystyle {\frac {\Delta v}{v}}={\frac {\Delta r}{r}}={\frac {v\Delta t}{r}}={\frac {v^{2}}{r}}=r\omega ^{2}}
a
=
Δ
v
Δ
t
=
v
2
r
=
r
ω
2
{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {v^{2}}{r}}=r\omega ^{2}}
v
=
a
r
{\displaystyle v={\sqrt {ar}}}
Vòng tròn bán kín r
v
=
r
ω
{\displaystyle v=r\omega }
a
=
r
α
{\displaystyle a=r\alpha }
s
=
r
θ
{\displaystyle s=r\theta }
Vòng tròn bán kín 1 đơn vị
v
=
ω
{\displaystyle v=\omega }
a
=
α
{\displaystyle a=\alpha }
s
=
θ
{\displaystyle s=\theta }
[ sửa ]
F
a
=
F
y
{\displaystyle F_{a}=F_{y}}
m
a
=
−
k
x
{\displaystyle ma=-kx}
a
=
−
k
m
x
{\displaystyle a=-{\frac {k}{m}}x}
d
2
d
t
2
x
=
−
k
m
x
{\displaystyle {\frac {d^{2}}{dt^{2}}}x=-{\frac {k}{m}}x}
x
=
A
sin
(
ω
t
)
{\displaystyle x=A\sin(\omega t)}
ω
=
k
m
{\displaystyle \omega ={\sqrt {\frac {k}{m}}}}
[ sửa ]
−
F
g
=
F
y
{\displaystyle -F_{g}=F_{y}}
−
m
g
=
k
y
{\displaystyle -mg=ky}
g
=
−
k
m
y
=
d
2
d
t
2
y
=
−
k
m
y
{\displaystyle g=-{\frac {k}{m}}y={\frac {d^{2}}{dt^{2}}}y=-{\frac {k}{m}}y}
y
=
A
sin
(
ω
t
)
{\displaystyle y=A\sin(\omega t)}
ω
=
k
m
{\displaystyle \omega ={\sqrt {\frac {k}{m}}}}
d
2
d
t
2
y
=
−
k
m
y
{\displaystyle {\frac {d^{2}}{dt^{2}}}y=-{\frac {k}{m}}y}
y
=
A
sin
(
ω
t
)
{\displaystyle y=A\sin(\omega t)}
ω
=
k
m
{\displaystyle \omega ={\sqrt {\frac {k}{m}}}}
[ sửa ]
−
F
g
=
F
θ
{\displaystyle -F_{g}=F_{\theta }}
−
m
g
=
l
θ
{\displaystyle -m_{g}=l\theta }
g
=
−
l
m
{\displaystyle g=-{\frac {l}{m}}}
d
2
d
t
2
θ
=
−
l
g
θ
{\displaystyle {\frac {d^{2}}{dt^{2}}}\theta =-{\frac {l}{g}}\theta }
y
=
A
sin
ω
t
{\displaystyle y=A\sin \omega t}
ω
=
l
m
{\displaystyle \omega ={\sqrt {\frac {l}{m}}}}
Mọi dao động sóng sin đều có một hàm số sóng là nghiệm của một phương trình sóng
Hàm số sóng
f
(
t
)
=
A
s
i
n
ω
t
{\displaystyle f(t)=Asin\omega t}
Phương trình sóng
f
″
(
t
)
=
−
β
f
(
t
)
{\displaystyle f^{''}(t)=-\beta f(t)}
ω
=
β
{\displaystyle \omega ={\sqrt {\beta }}}
ω
=
k
m
{\displaystyle \omega ={\sqrt {\frac {k}{m}}}}
ω
=
l
m
{\displaystyle \omega ={\sqrt {\frac {l}{m}}}}
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
v
{\displaystyle v}
m/s
Gia tốc
a
{\displaystyle a}
v
t
{\displaystyle {\frac {v}{t}}}
m/s2
Đường dài
s
{\displaystyle s}
v
t
{\displaystyle vt}
m
Lực
F
{\displaystyle F}
m
a
=
m
v
t
=
p
t
{\displaystyle ma=m{\frac {v}{t}}={\frac {p}{t}}}
N
Năng lực
W
{\displaystyle W}
F
s
=
p
t
s
=
p
v
{\displaystyle Fs={\frac {p}{t}}s=pv}
N m
Năng lượng
E
{\displaystyle E}
W
t
=
p
v
t
=
p
a
{\displaystyle {\frac {W}{t}}={\frac {pv}{t}}=pa}
N m/s
Tính Chất uyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
C
=
λ
f
{\displaystyle C=\lambda f}
m/s
Gia tốc
a
{\displaystyle a}
C
t
{\displaystyle {\frac {C}{t}}}
m/s2
Đường dài
s
{\displaystyle s}
C
t
{\displaystyle Ct}
m
Lực
F
{\displaystyle F}
p
t
=
h
λ
t
=
h
f
λ
{\displaystyle {\frac {p}{t}}={\frac {\frac {h}{\lambda }}{t}}={\frac {hf}{\lambda }}}
N
Năng lực
W
{\displaystyle W}
p
C
=
h
f
{\displaystyle pC=hf}
N m
Năng lượng
E
{\displaystyle E}
p
C
t
{\displaystyle p{\frac {C}{t}}}
N m/s
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
C
β
{\displaystyle C\beta }
m/s
Gia tốc
a
{\displaystyle a}
C
t
β
{\displaystyle {\frac {C}{t}}\beta }
m/s2
Đường dài
s
{\displaystyle s}
C
t
β
{\displaystyle Ct\beta }
m
Lực
F
{\displaystyle F}
p
t
β
{\displaystyle {\frac {p}{t}}\beta }
N
Năng lực
W
{\displaystyle W}
p
v
β
{\displaystyle pv\beta }
N m
Năng lượng
E
{\displaystyle E}
p
a
β
{\displaystyle pa\beta }
N m/s
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Gia tốc
a
{\displaystyle a}
v
−
v
o
t
−
t
o
=
Δ
v
Δ
t
{\displaystyle {\frac {v-v_{o}}{t-t_{o}}}={\frac {\Delta v}{\Delta t}}}
m/s2
Vận tốc
v
{\displaystyle v}
v
o
+
a
Δ
t
{\displaystyle v_{o}+a\Delta t}
m/s
Đường dài
s
{\displaystyle s}
Δ
t
(
v
o
+
Δ
v
)
=
Δ
t
(
v
o
+
a
Δ
t
)
=
Δ
t
(
v
−
a
Δ
t
)
=
v
2
−
v
o
2
2
a
{\displaystyle \Delta t(v_{o}+\Delta v)=\Delta t(v_{o}+a\Delta t)=\Delta t(v-a\Delta t)={\frac {v^{2}-v_{o}^{2}}{2a}}}
m
Lực
F
{\displaystyle F}
m
a
=
m
Δ
v
Δ
t
{\displaystyle ma=m{\frac {\Delta v}{\Delta t}}}
N
Năng lực
W
{\displaystyle W}
F
s
=
F
Δ
t
(
v
o
+
Δ
v
)
{\displaystyle Fs=F\Delta t(v_{o}+\Delta v)}
N m
Năng lượng
E
{\displaystyle E}
W
t
=
F
(
v
o
+
Δ
v
)
{\displaystyle {\frac {W}{t}}=F(v_{o}+\Delta v)}
N m/s
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
v
{\displaystyle v}
m/s
Gia tốc
a
{\displaystyle a}
v
t
{\displaystyle {\frac {v}{t}}}
m/s2
Đường dài
s
{\displaystyle s}
v
t
{\displaystyle vt}
m
Lực
F
{\displaystyle F}
m
v
t
{\displaystyle m{\frac {v}{t}}}
N
Năng lực
W
{\displaystyle W}
F
v
t
{\displaystyle Fvt}
N m
Năng lượng
E
{\displaystyle E}
F
v
{\displaystyle Fv}
N m/s
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Gia tốc
a
{\displaystyle a}
−
g
{\displaystyle -g}
m/s2
Vận tốc
v
{\displaystyle v}
−
g
t
{\displaystyle -gt}
m/s
Đường dài
s
{\displaystyle s}
−
g
t
2
{\displaystyle -gt^{2}}
m
Lực
F
{\displaystyle F}
−
m
g
{\displaystyle -mg}
N
Năng lực
W
{\displaystyle W}
−
m
g
h
{\displaystyle -mgh}
N m
Năng lượng
E
{\displaystyle E}
−
m
g
h
t
{\displaystyle -{\frac {mgh}{t}}}
N m/s
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
v
(
t
)
{\displaystyle v(t)}
m/s
Gia tốc
a
{\displaystyle a}
d
d
t
v
(
t
)
{\displaystyle {\frac {d}{dt}}v(t)}
m/s2
Đường dài
s
{\displaystyle s}
∫
v
(
t
)
d
t
{\displaystyle \int v(t)dt}
m
Lực
F
{\displaystyle F}
m
d
d
t
v
(
t
)
{\displaystyle m{\frac {d}{dt}}v(t)}
N
Năng lực
W
{\displaystyle W}
F
∫
v
(
t
)
d
t
{\displaystyle F\int v(t)dt}
N m
Năng lượng
E
{\displaystyle E}
F
t
∫
v
(
t
)
d
t
{\displaystyle {\frac {F}{t}}\int v(t)dt}
N m/s
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Đường dài
s
{\displaystyle s}
s
(
t
)
{\displaystyle s(t)}
m
Vận tốc
v
{\displaystyle v}
d
d
t
s
(
t
)
{\displaystyle {\frac {d}{dt}}s(t)}
m/s
Gia tốc
a
{\displaystyle a}
d
2
d
t
2
s
(
t
)
{\displaystyle {\frac {d^{2}}{dt^{2}}}s(t)}
m/s2
Lực
F
{\displaystyle F}
m
a
=
m
d
2
d
t
2
s
(
t
)
{\displaystyle ma=m{\frac {d^{2}}{dt^{2}}}s(t)}
N
Năng lực
W
{\displaystyle W}
p
v
=
p
d
d
t
s
(
t
)
{\displaystyle pv=p{\frac {d}{dt}}s(t)}
N m
Năng lượng
E
{\displaystyle E}
p
a
=
p
d
2
d
t
2
s
(
t
)
{\displaystyle pa=p{\frac {d^{2}}{dt^{2}}}s(t)}
N m/s
Chuyển động tròn là một lọai Chuyển động tuần hoàn cuả một điểm ở một khoảng cách không đổi so với một tâm điểm
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Đường dài
s
{\displaystyle s}
2
π
{\displaystyle 2\pi }
m
Vận tốc
v
{\displaystyle v}
2
π
t
=
2
π
f
=
ω
{\displaystyle {\frac {2\pi }{t}}=2\pi f=\omega }
m/s
Gia tốc
a
{\displaystyle a}
ω
t
{\displaystyle {\frac {\omega }{t}}}
m/s2
Lực
F
{\displaystyle F}
m
a
=
m
ω
t
{\displaystyle ma=m{\frac {\omega }{t}}}
N
Năng lực
W
{\displaystyle W}
F
s
=
p
v
=
p
ω
{\displaystyle Fs=pv=p\omega }
N m
Năng lượng
E
{\displaystyle E}
W
t
=
p
a
=
p
ω
t
{\displaystyle {\frac {W}{t}}=pa={\frac {p\omega }{t}}}
N m/s
[ sửa ]
Tính Chất Chuyển Động Ký Hiệu Công Thức Đơn vị
Vận tốc
v
{\displaystyle v}
r
α
{\displaystyle r\alpha }
m/s
Gia tốc
a
{\displaystyle a}
r
ω
{\displaystyle r\omega }
m/s2
Đường dài
s
{\displaystyle s}
r
θ
{\displaystyle r\theta }
m
Lực
F
{\displaystyle F}
m
a
=
m
r
α
{\displaystyle ma=mr\alpha }
N
Năng lực
W
{\displaystyle W}
P
v
=
p
r
ω
{\displaystyle Pv=pr\omega }
N m
Năng lượng
E
{\displaystyle E}
P
a
=
p
r
ω
t
{\displaystyle Pa={\frac {pr\omega }{t}}}
N m/s
Dao động một loại chuyển động tuần hoàn của một vật quanh một vị trí cân bằng lập đi lập lại trong một chu kỳ thời gian . Thí dụ như Dao động lò xo , Dao động con lắc , Dao động điện , Dao động điện từ
[ sửa ]
−
F
g
=
F
y
{\displaystyle -F_{g}=F_{y}}
−
m
g
=
k
y
{\displaystyle -mg=ky}
g
=
−
β
y
=
d
2
d
t
2
y
{\displaystyle g=-\beta y={\frac {d^{2}}{dt^{2}}}y}
y
=
A
s
i
n
ω
t
{\displaystyle y=Asin\omega t}
ω
=
β
=
k
m
{\displaystyle \omega ={\sqrt {\beta }}={\sqrt {\frac {k}{m}}}}
[ sửa ]
F
a
=
−
F
x
{\displaystyle F_{a}=-F_{x}}
m
a
=
−
k
x
{\displaystyle ma=-kx}
a
=
−
β
x
=
d
2
d
t
2
x
{\displaystyle a=-\beta x={\frac {d^{2}}{dt^{2}}}x}
x
=
A
s
i
n
ω
t
{\displaystyle x=Asin\omega t}
ω
=
β
=
k
m
{\displaystyle \omega ={\sqrt {\beta }}={\sqrt {\frac {k}{m}}}}
[ sửa ]
−
F
g
=
F
θ
{\displaystyle -F_{g}=F_{\theta }}
−
m
g
=
l
θ
{\displaystyle -mg=l\theta }
−
g
=
−
β
θ
=
d
2
d
t
2
θ
{\displaystyle -g=-\beta \theta ={\frac {d^{2}}{dt^{2}}}\theta }
θ
=
A
s
i
n
ω
t
{\displaystyle \theta =Asin\omega t}
ω
=
β
=
l
m
{\displaystyle \omega ={\sqrt {\beta }}={\sqrt {\frac {l}{m}}}}
[ sửa ]
Tính chất chuyển động sóng Ký hiệu Công thức
Đường dài
s
{\displaystyle s}
k
λ
{\displaystyle k\lambda }
Thời gian
t
{\displaystyle t}
t
{\displaystyle t}
Vận tốc
v
{\displaystyle v}
v
=
k
λ
t
=
k
λ
f
=
k
ω
{\displaystyle v={\frac {k\lambda }{t}}=k\lambda f=k\omega }
Số sóng
k
{\displaystyle k}
k
=
s
λ
=
v
ω
{\displaystyle k={\frac {s}{\lambda }}={\frac {v}{\omega }}}
Vận tốc góc
ω
{\displaystyle \omega }
ω
=
λ
f
=
v
k
{\displaystyle \omega =\lambda f={\frac {v}{k}}}
Bước sóng
λ
{\displaystyle \lambda }
λ
=
ω
f
=
ω
t
=
s
k
{\displaystyle \lambda ={\frac {\omega }{f}}=\omega t={\frac {s}{k}}}
Tần số sóng
f
{\displaystyle f}
f
=
ω
λ
=
v
k
λ
=
1
t
{\displaystyle f={\frac {\omega }{\lambda }}={\frac {v}{k\lambda }}={\frac {1}{t}}}
Phương trình sóng
f
n
(
t
)
{\displaystyle f^{n}(t)}
d
n
d
t
n
f
(
t
)
=
−
β
f
(
t
)
{\displaystyle {\frac {d^{n}}{dt^{n}}}f(t)=-\beta f(t)}
Hàm số sóng
f
(
t
)
{\displaystyle f(t)}
f
(
t
)
=
A
s
i
n
ω
t
{\displaystyle f(t)=Asin\omega t}
Vận tốc góc
ω
=
β
n
=
λ
f
=
v
k
{\displaystyle \omega ={\sqrt[{n}]{\beta }}=\lambda f={\frac {v}{k}}}
n ≥ 2
[ sửa ] Lực hút giửa điện tích khác loại
F
=
K
Q
+
Q
−
r
2
{\displaystyle F=K{\frac {Q_{+}Q_{-}}{r^{2}}}}
Lực hút giửa điện tích đồng loại
F
=
K
Q
2
r
2
{\displaystyle F=K{\frac {Q^{2}}{r^{2}}}}
Q
+
=
Q
−
=
Q
{\displaystyle Q_{+}=Q_{-}=Q}
E
=
F
Q
=
K
Q
r
2
{\displaystyle E={\frac {F}{Q}}={\frac {KQ}{r^{2}}}}
W
=
∫
E
d
r
=
K
Q
r
{\displaystyle W=\int Edr={\frac {KQ}{r}}}
U
=
W
t
=
K
Q
r
t
{\displaystyle U={\frac {W}{t}}={\frac {KQ}{rt}}}
r
=
K
Q
2
F
{\displaystyle r={\sqrt {\frac {KQ^{2}}{F}}}}
Lực điện làm cho điện tích đứng yên di chuyển
F
=
Q
E
{\displaystyle F=QE}
F
=
Q
E
=
Q
V
l
=
W
l
{\displaystyle F=QE=Q{\frac {V}{l}}={\frac {W}{l}}}
l
=
W
F
{\displaystyle l={\frac {W}{F}}}
v
=
l
t
=
W
F
t
=
U
F
{\displaystyle v={\frac {l}{t}}={\frac {W}{Ft}}={\frac {U}{F}}}
t
=
l
v
=
W
F
/
U
F
=
W
F
×
F
U
=
W
U
{\displaystyle t={\frac {l}{v}}={\frac {W}{F}}/{\frac {U}{F}}={\frac {W}{F}}\times {\frac {F}{U}}={\frac {W}{U}}}
Lực điện làm cho điện tích di chuyển theo hướng dọc
F
=
±
Q
v
B
{\displaystyle F=\pm QvB}
F
=
Q
v
B
=
I
t
v
B
=
I
l
B
{\displaystyle F=QvB=ItvB=IlB}
l
=
F
I
B
{\displaystyle l={\frac {F}{IB}}}
v
=
F
Q
v
{\displaystyle v={\frac {F}{Qv}}}
t
=
l
v
=
F
I
B
/
F
Q
v
=
F
I
B
×
Q
v
F
=
Q
v
I
B
{\displaystyle t={\frac {l}{v}}={\frac {F}{IB}}/{\frac {F}{Qv}}={\frac {F}{IB}}\times {\frac {Qv}{F}}={\frac {Qv}{IB}}}
Lực điện làm cho điện tích di chuyển theo hướng nghiêng
F
=
Q
(
E
±
v
B
)
{\displaystyle F=Q(E\pm vB)}
Khi
v
=
0
{\displaystyle v=0}
F
=
Q
(
E
±
v
B
)
=
Q
E
{\displaystyle F=Q(E\pm vB)=QE}
Khi v ≠ 0 ,
Q
E
=
0
{\displaystyle QE=0}
F
=
Q
(
E
±
v
B
)
=
Q
v
B
{\displaystyle F=Q(E\pm vB)=QvB}
Khi
E
±
v
B
=
0
{\displaystyle E\pm vB=0}
F
=
Q
(
E
±
v
B
)
=
0
{\displaystyle F=Q(E\pm vB)=0}
E
=
v
B
{\displaystyle E=vB}
B
=
1
v
B
{\displaystyle B={\frac {1}{v}}B}
v
=
E
B
{\displaystyle v={\frac {E}{B}}}
Đừong dài đường thẳng nghiêng
l
=
l
E
2
+
l
B
2
=
(
Q
v
F
)
2
+
(
F
I
B
)
2
{\displaystyle l={\sqrt {l_{E}^{2}+l_{B}^{2}}}={\sqrt {({\frac {Qv}{F}})^{2}+({\frac {F}{IB}})^{2}}}}
Tổng lực làm cho điện tích di chuyển theo vòng tròn
F
p
=
F
B
{\displaystyle F_{p}=F_{B}}
m
v
2
r
=
Q
v
B
{\displaystyle m{\frac {v^{2}}{r}}=QvB}
Q
m
=
v
2
r
v
B
=
v
r
B
{\displaystyle {\frac {Q}{m}}={\frac {v^{2}}{rvB}}={\frac {v}{rB}}}
r
=
m
v
2
Q
B
{\displaystyle r={\frac {mv^{2}}{QB}}}
[ sửa ] [ sửa ]
h
f
=
h
f
o
+
1
2
m
v
2
{\displaystyle hf=hf_{o}+{\frac {1}{2}}mv^{2}}
v
=
2
h
Δ
f
m
{\displaystyle v={\sqrt {\frac {2h\Delta f}{m}}}}
h
=
m
v
2
2
Δ
f
{\displaystyle h={\frac {mv^{2}}{2\Delta f}}}
Δ
f
=
f
−
f
o
=
f
−
C
Λ
o
=
f
−
3
×
10
8
m
/
s
400
−
700
n
m
{\displaystyle \Delta f=f-f_{o}=f-{\frac {C}{\Lambda _{o}}}=f-{\frac {3\times 10^{8}m/s}{400-700nm}}}
[ sửa ]
n
h
f
=
m
v
r
(
2
π
)
{\displaystyle nhf=mvr(2\pi )}
v
=
(
1
2
π
)
(
n
h
f
m
r
)
{\displaystyle v=({\frac {1}{2\pi }})({\frac {nhf}{mr}})}
ℏ
=
h
2
π
=
m
v
r
n
f
{\displaystyle \hbar ={\frac {h}{2\pi }}={\frac {mvr}{nf}}}
F
=
k
Q
+
Q
−
r
2
=
k
Z
e
2
r
2
{\displaystyle F=k{\frac {Q_{+}Q_{-}}{r^{2}}}=k{\frac {Ze^{2}}{r^{2}}}}
Cho lực Coulomb bằng lực ly tâm
k
Z
e
2
r
2
=
m
v
2
r
{\displaystyle k{\frac {Ze^{2}}{r^{2}}}={\frac {mv^{2}}{r}}}
k
Z
e
2
=
m
v
2
r
{\displaystyle kZe^{2}=mv^{2}r}
r
=
k
Z
e
2
m
v
2
{\displaystyle r={\frac {kZe^{2}}{mv^{2}}}}
Bohr điều kiện để lượng tử hóa của góc độn lượng
m
v
r
=
n
h
2
π
{\displaystyle mvr={\frac {nh}{2\pi }}}
Giải tìm v
v
=
n
h
2
π
m
r
{\displaystyle v={\frac {nh}{2\pi mr}}}
Thế v vào r
r
=
k
Z
e
2
m
(
n
h
2
π
m
r
)
2
{\displaystyle r={\frac {kZe^{2}}{m({\frac {nh}{2\pi mr}})^{2}}}}
r
=
k
Z
e
2
m
4
π
2
m
2
r
2
n
2
h
2
{\displaystyle r={\frac {kZe^{2}}{m}}{\frac {4\pi ^{2}m^{2}r^{2}}{n^{2}h^{2}}}}
1
=
4
π
2
k
Z
e
2
m
2
m
n
2
h
2
r
{\displaystyle 1={\frac {4\pi ^{2}kZe^{2}m^{2}}{mn^{2}h^{2}}}r}
r
=
n
2
h
2
4
π
2
k
Z
e
2
m
=
n
2
ℏ
2
m
k
Z
e
2
{\displaystyle r={\frac {n^{2}h^{2}}{4\pi ^{2}kZe^{2}m}}={\frac {n^{2}\hbar ^{2}}{mkZe^{2}}}}
Với Hydrogen Z=1, n=1
r
1
=
0.0529177
n
m
{\displaystyle r_{1}=0.0529177nm}
Bohr radius [ sửa ]
E
=
1
2
m
v
2
−
k
Q
+
Q
−
r
2
{\displaystyle E={\frac {1}{2}}mv^{2}-k{\frac {Q_{+}Q_{-}}{r^{2}}}}
E
=
1
2
m
v
2
−
k
Z
e
2
r
2
{\displaystyle E={\frac {1}{2}}mv^{2}-k{\frac {Ze^{2}}{r^{2}}}}
m
v
2
r
=
k
Z
e
2
r
2
{\displaystyle {\frac {mv^{2}}{r}}=k{\frac {Ze^{2}}{r^{2}}}}
m
v
2
r
r
2
=
k
Z
e
2
r
2
r
2
{\displaystyle {\frac {mv^{2}}{r}}{\frac {r}{2}}=k{\frac {Ze^{2}}{r^{2}}}{\frac {r}{2}}}
1
2
m
v
2
=
k
Z
e
2
2
r
{\displaystyle {\frac {1}{2}}mv^{2}=k{\frac {Ze^{2}}{2r}}}
E
=
k
Z
e
2
2
r
−
k
Z
e
2
r
=
−
k
Z
e
2
2
r
{\displaystyle E=k{\frac {Ze^{2}}{2r}}-k{\frac {Ze^{2}}{r}}=-{\frac {kZe^{2}}{2r}}}
Với Hydrogen Z=1
E
=
−
13.6
e
V
n
2
{\displaystyle E=-{\frac {13.6eV}{n^{2}}}}
n được biết là số lượng tử Principal quantum number
h
f
=
E
3
−
E
2
=
−
13.6
e
V
3
2
−
−
13.6
e
V
2
2
{\displaystyle hf=E_{3}-E_{2}={\frac {-13.6eV}{3^{2}}}-{\frac {-13.6eV}{2^{2}}}}
h
f
=
E
3
−
E
2
=
−
1.511
e
V
+
3.40
e
V
=
1.89
e
V
{\displaystyle hf=E_{3}-E_{2}=-1.511eV+3.40eV=1.89eV}
f
=
1.89
e
V
h
(
1.6
×
10
−
19
e
V
)
=
4.56
×
10
1
4
{\displaystyle f={\frac {1.89eV}{h}}({\frac {1.6\times 10^{-}{19}}{eV}})=4.56\times 10^{1}4}
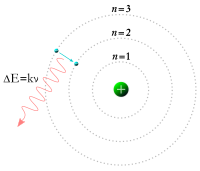
Δ
E
=
E
n
−
E
n
−
1
=
n
h
f
=
n
h
C
λ
{\displaystyle \Delta E=E_{n}-E_{n-1}=nhf=nh{\frac {C}{\lambda }}}
1
λ
=
Δ
E
n
h
C
{\displaystyle {\frac {1}{\lambda }}={\frac {\Delta E}{nhC}}}
Vạch sáng Lyman
1
λ
=
R
(
1
1
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{1^{2}}}-{\frac {1}{n^{2}}})}
Vạch sáng Balmer
1
λ
=
R
(
1
2
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}})}
Vạch sáng Paschen
1
λ
=
R
(
1
3
2
−
1
n
2
)
{\displaystyle {\frac {1}{\lambda }}=R({\frac {1}{3^{2}}}-{\frac {1}{n^{2}}})}























































![{\displaystyle s=\Delta t[v(t)+{\frac {\Delta v(t)}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1acad5dd6028c5595390584e41fc17653daa97b6)

















































































































![{\displaystyle \omega ={\sqrt[{n}]{\beta }}=\lambda f={\frac {v}{k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce7e1cbca181865783e19d55f2d9a85d4564ad4c)
































































