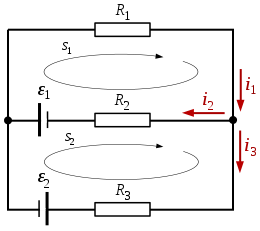
[ sửa ] Tổng giá trị đại số của dòng điện tại một nút trong một mạch điện là bằng không . Tại bất kỳ nút (ngã rẽ) nào trong một mạch điện, thì tổng cường độ dòng điện chạy đến nút phải bằng tổng cường độ dòng điện từ nút chạy đi
∑
k
=
1
n
I
k
=
0
{\displaystyle \sum _{k=1}^{n}{I}_{k}=0}
n là tổng số các nhánh với dòng điện chạy vào nút hay từ nút ra.
∑
k
=
1
n
I
~
k
=
0
{\displaystyle \sum _{k=1}^{n}{\tilde {I}}_{k}=0}
[ sửa ] Tổng giá trị điện áp dọc theo một vòng bằng không
∑
k
=
1
n
V
k
=
0
{\displaystyle \sum _{k=1}^{n}V_{k}=0}
n là tổng số các điện áp được đo.
∑
k
=
1
n
V
~
k
=
0
{\displaystyle \sum _{k=1}^{n}{\tilde {V}}_{k}=0}
Theo định luật 1, ta có:
i
1
−
i
2
−
i
3
=
0
{\displaystyle i_{1}-i_{2}-i_{3}=0\,}
Định luật 2 áp dụng cho vòng s 1 :
−
R
2
i
2
+
ϵ
1
−
R
1
i
1
=
0
{\displaystyle -R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}=0}
Định luật 2 áp dụng cho vòng s 2 :
−
R
3
i
3
−
ϵ
2
−
ϵ
1
+
R
2
i
2
=
0
{\displaystyle -R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}=0}
Đến đây ta có hệ phương trình tuyến tính cho 3 ẩn số
i
1
,
i
2
,
i
3
{\displaystyle i_{1},i_{2},i_{3}}
{
i
1
−
i
2
−
i
3
=
0
−
R
2
i
2
+
ϵ
1
−
R
1
i
1
=
0
−
R
3
i
3
−
ϵ
2
−
ϵ
1
+
R
2
i
2
=
0
{\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}&=0\\\end{cases}}}
Giả sử:
R
1
=
100
,
R
2
=
200
,
R
3
=
300
(ohm)
;
ϵ
1
=
3
,
ϵ
2
=
4
(volt)
{\displaystyle R_{1}=100,\ R_{2}=200,\ R_{3}=300{\text{ (ohm)}};\ \epsilon _{1}=3,\ \epsilon _{2}=4{\text{ (volt)}}}
kết quả:
{
i
1
=
1
1100
hay
0.
90
¯
mA
i
2
=
4
275
hay
14.
54
¯
mA
i
3
=
−
3
220
hay
−
13.
63
¯
mA
{\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{ hay }}0.{\bar {90}}{\text{ mA}}\\i_{2}={\frac {4}{275}}{\text{ hay }}14.{\bar {54}}{\text{ mA}}\\i_{3}=-{\frac {3}{220}}{\text{ hay }}-13.{\bar {63}}{\text{ mA}}\\\end{cases}}}
i
3
{\displaystyle i_{3}}
i
3
{\displaystyle i_{3}}