[ sửa ] Mạch điện của nhiều điện trở mắc nối kề nhau
Khi mắc nối tiếp nhiều điện trở lại với nhau, tổng của các điện trở sẻ tăng và bằng với tổng điện kháng của các Điện trở
R
e
q
=
R
1
+
R
2
+
R
3
+
.
.
.
+
R
n
{\displaystyle R_{eq}=R_{1}+R_{2}+R_{3}+...+R_{n}\,}
Khi mắc n điện trở cùng giá trị nối tiếp với nhau, Điện Kháng sẻ tăng gấp n
R
e
q
=
R
1
+
R
2
+
.
.
.
+
R
n
=
R
+
R
+
.
.
.
+
R
=
n
R
{\displaystyle R_{eq}=R_{1}+R_{2}+...+R_{n}=R+R+...+R=nR}
[ sửa ] Khi mắc song song nhiều điện trở lại với nhau, tổng của các điện trở sẻ giảm và bằng
1
R
e
q
=
1
R
1
+
1
R
2
+
.
.
.
+
1
R
n
{\displaystyle {\frac {1}{R_{eq}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+...+{\frac {1}{R_{n}}}\,}
Khi mắc n điện trở cùng giá trị song song với nhau, Điện Kháng sẻ giảm gấp n
1
R
e
q
=
1
R
1
+
1
R
2
+
.
.
.
+
1
R
n
=
1
R
+
1
R
+
.
.
.
+
1
R
=
1
n
R
{\displaystyle {\frac {1}{R_{eq}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+...+{\frac {1}{R_{n}}}={\frac {1}{R}}+{\frac {1}{R}}+...+{\frac {1}{R}}={\frac {1}{n}}R}
[ sửa ]
i
=
V
R
2
+
R
1
{\displaystyle i={\frac {V}{R_{2}+R_{1}}}}
V
o
=
i
R
2
=
R
i
v
i
R
2
+
R
1
{\displaystyle V_{o}=iR_{2}=R_{i}{\frac {v_{i}}{R_{2}+R_{1}}}}
V
o
V
i
=
R
2
R
2
+
R
1
{\displaystyle {\frac {V_{o}}{V_{i}}}={\frac {R_{2}}{R_{2}+R_{1}}}}
V
o
V
i
=
R
2
R
2
+
R
1
{\displaystyle {\frac {V_{o}}{V_{i}}}={\frac {R_{2}}{R_{2}+R_{1}}}}
V
=
V
2
R
1
R
1
+
R
3
=
V
1
R
1
R
2
+
R
1
{\displaystyle V=V_{2}{\frac {R_{1}}{R_{1}+R_{3}}}=V_{1}{\frac {R_{1}}{R_{2}+R_{1}}}}
V
2
V
1
=
R
1
+
R
3
R
1
R
1
R
2
+
R
3
{\displaystyle {\frac {V_{2}}{V_{1}}}={\frac {R_{1}+R_{3}}{R_{1}}}{\frac {R_{1}}{R_{2}+R_{3}}}}
V
2
V
1
=
R
1
+
R
3
R
2
+
R
3
{\displaystyle {\frac {V_{2}}{V_{1}}}={\frac {R_{1}+R_{3}}{R_{2}+R_{3}}}}
i
1
=
i
2
+
i
3
{\displaystyle i_{1}=i_{2}+i_{3}}
v
i
R
1
=
v
i
−
v
o
R
2
+
v
o
R
3
{\displaystyle {\frac {v_{i}}{R_{1}}}={\frac {v_{i}-v_{o}}{R_{2}}}+{\frac {v_{o}}{R_{3}}}}
v
i
v
o
=
(
R
3
R
1
)
(
R
2
−
R
1
R
2
−
R
3
)
{\displaystyle {\frac {v_{i}}{v_{o}}}=({\frac {R_{3}}{R_{1}}})({\frac {R_{2}-R_{1}}{R_{2}-R_{3}}})}
v
o
v
i
=
(
R
3
R
1
)
(
R
2
−
R
1
R
2
−
R
3
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=({\frac {R_{3}}{R_{1}}})({\frac {R_{2}-R_{1}}{R_{2}-R_{3}}})}
[ sửa ]
R
E
Q
=
(
R
1
‖
R
2
)
+
R
3
{\displaystyle R_{EQ}=(R_{1}\|R_{2})+R_{3}}
R
E
Q
=
R
1
R
2
R
1
+
R
2
+
R
3
{\displaystyle R_{EQ}={R_{1}R_{2} \over R_{1}+R_{2}}+R_{3}}
Δ - Y Hoán Chuyển
R
1
=
R
a
R
b
R
a
+
R
b
+
R
c
{\displaystyle R_{1}={\frac {R_{\mathrm {a} }R_{\mathrm {b} }}{R_{\mathrm {a} }+R_{\mathrm {b} }+R_{\mathrm {c} }}}}
R
2
=
R
b
R
c
R
a
+
R
b
+
R
c
{\displaystyle R_{2}={\frac {R_{\mathrm {b} }R_{\mathrm {c} }}{R_{\mathrm {a} }+R_{\mathrm {b} }+R_{\mathrm {c} }}}}
R
3
=
R
c
R
a
R
a
+
R
b
+
R
c
{\displaystyle R_{3}={\frac {R_{\mathrm {c} }R_{\mathrm {a} }}{R_{\mathrm {a} }+R_{\mathrm {b} }+R_{\mathrm {c} }}}}
Y - Δ Hoán Chuyển
R
a
=
R
1
R
2
+
R
2
R
3
+
R
3
R
1
R
2
{\displaystyle R_{\mathrm {a} }={\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{2}}}}
R
b
=
R
1
R
2
+
R
2
R
3
+
R
3
R
1
R
3
{\displaystyle R_{\mathrm {b} }={\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{3}}}}
R
c
=
R
1
R
2
+
R
2
R
3
+
R
3
R
1
R
1
{\displaystyle R_{\mathrm {c} }={\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{1}}}}
Mạch điện RL là mạch điện điện tử có 2 linh kiện tử Điện trở R và Tụ điện L cùng với các lối mắc để tạo ra một bộ phận điện tử có khả năng thực thi một việc
[ sửa ]
V
L
+
V
R
=
0
{\displaystyle V_{L}+V_{R}=0}
L
d
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {di}{dt}}+iR=0}
d
i
d
t
+
i
R
L
=
0
{\displaystyle {\frac {di}{dt}}+i{\frac {R}{L}}=0}
d
i
d
t
=
−
1
T
i
{\displaystyle {\frac {di}{dt}}=-{\frac {1}{T}}i}
i
=
A
e
−
t
T
{\displaystyle i=Ae^{-{\frac {t}{T}}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
Mạch điện RL nối tiếp cho một Hàm số giảm thiểu điện thỏa mản một Phương trình giảm thiểu điện
[ sửa ]
v
o
v
i
=
R
R
+
j
ω
L
=
1
1
+
j
ω
L
R
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega L}}={\frac {1}{1+j\omega {\frac {L}{R}}}}={\frac {1}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
[ sửa ]
v
o
v
i
=
j
ω
L
R
+
j
ω
L
=
j
ω
L
R
1
+
j
ω
L
R
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega L}{R+j\omega L}}={\frac {j\omega {\frac {L}{R}}}{1+j\omega {\frac {L}{R}}}}={\frac {j\omega T}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
=
2
π
f
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}=2\pi f}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
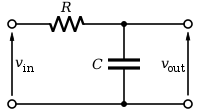
Mạch điện RC là mạch điện điện tử có 2 linh kiện tử Điện trở R và Tụ điện C cùng với các lối mắc để tạo ra một bộ phận điện tử có khả năng thực thi một việc
[ sửa ] Ở trạng thái cân bằng, tổng mạch điện của tụ điện và điện trở bằng không
C
d
v
(
t
)
d
t
+
v
(
t
)
R
=
0
{\displaystyle C{\frac {dv(t)}{dt}}+v(t)R=0}
d
v
(
t
)
d
t
=
−
1
T
v
(
t
)
R
{\displaystyle {\frac {dv(t)}{dt}}=-{\frac {1}{T}}v(t)R}
d
v
(
t
)
v
(
t
)
=
−
1
T
d
t
{\displaystyle {\frac {dv(t)}{v(t)}}=-{\frac {1}{T}}dt}
∫
d
v
(
t
)
v
(
t
)
=
−
1
T
∫
d
t
{\displaystyle \int {\frac {dv(t)}{v(t)}}=-{\frac {1}{T}}\int dt}
L
n
v
(
t
)
=
−
1
T
t
+
c
{\displaystyle Lnv(t)=-{\frac {1}{T}}t+c}
v
(
t
)
=
e
−
1
T
+
c
{\displaystyle v(t)=e^{-{\frac {1}{T}}+c}}
v
(
t
)
=
A
e
−
1
T
{\displaystyle v(t)=Ae^{-{\frac {1}{T}}}}
T
=
R
C
{\displaystyle T=RC}
[ sửa ]
v
o
v
i
=
j
ω
C
R
+
j
ω
C
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega C}{R+j\omega C}}={\frac {1}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
{\displaystyle \omega _{o}={\frac {1}{T}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
1
2
v
i
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {1}{2}}v_{i}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
[ sửa ]
v
o
v
i
=
R
R
+
j
ω
C
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega C}}={\frac {j\omega T}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
{\displaystyle \omega _{o}={\frac {1}{T}}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
1
2
v
i
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {1}{2}}v_{i}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
Mạch điện LC là mạch điện điện tử có 2 linh kiện tử Cuộn từ L và Tụ điện C cùng với các lối mắc để tạo ra một bộ phận điện tử có khả năng thực thi một việc
[ sửa ] Mạch điện RLC nối tiếp . Mạch điện điện tử của 3 linh kiện điện tử R, L và C mắc nối tiếp với nhau
[ sửa ] Mạch điện với R,C,L≠0
[ sửa ]
V
L
+
V
C
+
V
R
=
0
{\displaystyle V_{L}+V_{C}+V_{R}=0}
L
d
2
i
d
t
2
+
1
C
∫
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {d^{2}i}{dt^{2}}}+{\frac {1}{C}}\int idt+iR=0}
d
2
i
d
t
2
+
R
L
d
i
d
t
+
1
L
C
i
=
0
{\displaystyle {\frac {d^{2}i}{dt^{2}}}+{\frac {R}{L}}{\frac {di}{dt}}+{\frac {1}{LC}}i=0}
d
2
i
d
t
2
=
−
R
2
L
d
i
d
t
−
1
L
C
i
{\displaystyle {\frac {d^{2}i}{dt^{2}}}=-{\frac {R}{2L}}{\frac {di}{dt}}-{\frac {1}{LC}}i}
d
2
i
d
t
2
=
−
2
α
d
i
d
t
−
β
i
{\displaystyle {\frac {d^{2}i}{dt^{2}}}=-2\alpha {\frac {di}{dt}}-\beta i}
Nghiệm phương trình
Một nghiệm thực .
α
=
β
{\displaystyle \alpha =\beta }
i
=
A
e
−
α
t
=
A
(
α
)
{\displaystyle i=Ae^{-\alpha t}=A(\alpha )}
Hai nghiệm thực .
α
>
β
{\displaystyle \alpha >\beta }
i
=
A
e
(
−
α
±
λ
)
t
{\displaystyle i=Ae^{(-\alpha \pm \lambda )t}}
Hai nghiệm phức .
α
<
β
{\displaystyle \alpha <\beta }
i
=
A
e
(
−
α
±
j
ω
)
t
=
A
(
α
)
sin
ω
t
{\displaystyle i=Ae^{(-\alpha \pm j\omega )t}=A(\alpha )\sin \omega t}
A
(
α
)
=
A
e
−
α
t
{\displaystyle A(\alpha )=Ae^{-\alpha t}}
ω
=
β
−
α
{\displaystyle \omega ={\sqrt {\beta -\alpha }}}
λ
=
α
−
β
{\displaystyle \lambda ={\sqrt {\alpha -\beta }}}
β
=
1
T
=
1
L
C
{\displaystyle \beta ={\frac {1}{T}}={\frac {1}{LC}}}
α
=
β
γ
=
R
2
L
{\displaystyle \alpha =\beta \gamma ={\frac {R}{2L}}}
T
=
L
C
{\displaystyle T=LC}
γ
=
R
C
{\displaystyle \gamma =RC}
[ sửa ] R,C,L≠0
Z
C
=
−
Z
L
{\displaystyle Z_{C}=-Z_{L}}
Z
t
=
R
{\displaystyle Z_{t}=R}
i
(
ω
=
0
)
=
0
{\displaystyle i(\omega =0)=0}
i
(
ω
=
ω
o
)
=
v
R
{\displaystyle i(\omega =\omega _{o})={\frac {v}{R}}}
i
(
ω
=
00
)
=
0
{\displaystyle i(\omega =00)=0}
ω
o
=
1
T
{\displaystyle \omega _{o}={\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
Với R=0 mạch điện RLC nối tiếp trở thành mạch điện LC nối tiếp
[ sửa ]
V
L
+
V
C
=
0
{\displaystyle V_{L}+V_{C}=0}
L
d
2
i
d
t
2
+
1
C
∫
i
d
t
=
0
{\displaystyle L{\frac {d^{2}i}{dt^{2}}}+{\frac {1}{C}}\int idt=0}
d
2
i
d
t
2
+
1
L
C
i
=
0
{\displaystyle {\frac {d^{2}i}{dt^{2}}}+{\frac {1}{LC}}i=0}
d
2
i
d
t
2
=
−
1
T
i
{\displaystyle {\frac {d^{2}i}{dt^{2}}}=-{\frac {1}{T}}i}
i
=
A
e
−
1
T
t
=
A
e
±
j
ω
t
=
A
sin
ω
t
{\displaystyle i=Ae^{{\sqrt {-{\frac {1}{T}}}}t}=Ae^{\pm j\omega t}=A\sin \omega t}
ω
=
1
T
{\displaystyle \omega ={\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
Z
C
=
−
Z
L
{\displaystyle Z_{C}=-Z_{L}}
V
C
=
−
V
L
{\displaystyle V_{C}=-V_{L}}
v
(
θ
)
=
A
sin
(
ω
o
t
+
2
π
)
−
A
sin
(
ω
o
t
−
2
π
)
{\displaystyle v(\theta )=A\sin(\omega _{o}t+2\pi )-A\sin(\omega _{o}t-2\pi )}
ω
o
=
±
j
1
T
{\displaystyle \omega _{o}=\pm j{\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
Với L=0 mạch điện RLC nối tiếp trở thành mạch điện RC nối tiếp
Ở trạng thái cân bằng
v
C
+
v
R
=
0
{\displaystyle v_{C}+v_{R}=0}
C
d
v
d
t
+
v
R
=
0
{\displaystyle C{\frac {dv}{dt}}+{\frac {v}{R}}=0}
d
v
d
t
=
−
1
T
{\displaystyle {\frac {dv}{dt}}=-{\frac {1}{T}}}
d
v
v
=
−
1
T
d
t
{\displaystyle {\frac {dv}{v}}=-{\frac {1}{T}}dt}
∫
d
v
v
=
−
1
T
∫
d
t
{\displaystyle \int {\frac {dv}{v}}=-{\frac {1}{T}}\int dt}
L
n
v
=
−
1
T
t
+
c
{\displaystyle Lnv=-{\frac {1}{T}}t+c}
v
=
e
−
1
T
t
+
c
=
A
e
−
1
T
t
{\displaystyle v=e^{-{\frac {1}{T}}t+c}=Ae^{-{\frac {1}{T}}t}}
T
=
R
C
{\displaystyle T=RC}
Với C=0 mạch điện RLC nối tiếp trở thành mạch điện RL nối tiếp
Ở trạng thái cân bằng
v
L
+
v
R
=
0
{\displaystyle v_{L}+v_{R}=0}
L
d
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {di}{dt}}+iR=0}
d
i
d
t
=
−
1
T
{\displaystyle {\frac {di}{dt}}=-{\frac {1}{T}}}
d
i
i
=
−
1
T
d
t
{\displaystyle {\frac {di}{i}}=-{\frac {1}{T}}dt}
∫
d
i
v
=
−
1
T
∫
d
t
{\displaystyle \int {\frac {di}{v}}=-{\frac {1}{T}}\int dt}
L
n
i
=
−
1
T
t
+
c
{\displaystyle Lni=-{\frac {1}{T}}t+c}
i
=
e
−
1
T
t
+
c
=
A
e
−
1
T
t
{\displaystyle i=e^{-{\frac {1}{T}}t+c}=Ae^{-{\frac {1}{T}}t}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
[ sửa ] Với R=0 mạch điện RLC nối tiếp trở thành mạch điện của cuộn từ L
[ sửa ]
∇
2
E
=
−
ω
E
{\displaystyle \nabla ^{2}E=-\omega E}
∇
2
B
=
−
ω
B
{\displaystyle \nabla ^{2}B=-\omega B}
E
=
A
sin
ω
t
{\displaystyle E=A\sin \omega t}
B
=
A
sin
ω
t
{\displaystyle B=A\sin \omega t}
ω
=
1
T
{\displaystyle \omega ={\sqrt {\frac {1}{T}}}}
T
=
μ
ϵ
{\displaystyle T=\mu \epsilon }
[ sửa ]
∇
2
E
=
−
ω
o
E
{\displaystyle \nabla ^{2}E=-\omega _{o}E}
∇
2
B
=
−
ω
o
B
{\displaystyle \nabla ^{2}B=-\omega _{o}B}
E
=
A
sin
ω
o
t
{\displaystyle E=A\sin \omega _{o}t}
B
=
A
sin
ω
o
t
{\displaystyle B=A\sin \omega _{o}t}
ω
o
=
1
T
o
{\displaystyle \omega _{o}={\sqrt {\frac {1}{T_{o}}}}}
T
o
=
μ
o
ϵ
o
{\displaystyle T_{o}=\mu _{o}\epsilon _{o}}
[ sửa ] [ sửa ] Schematic of a 555 in monostable mode
Thời gian của sóng đơn , Thời gian để nạp điện bằng 2/3 điện cung cấp
t
=
R
C
ln
(
3
)
≈
1.1
R
C
{\displaystyle t=RC\ln(3)\approx 1.1RC}
Với
t,R, đo bằng đơn vị seconds, ohms và farads [ sửa ] Standard 555 Astable Circuit 1 , R2 and C:
f
=
1
ln
(
2
)
⋅
C
⋅
(
R
1
+
2
R
2
)
{\displaystyle f={\frac {1}{\ln(2)\cdot C\cdot (R_{1}+2R_{2})}}}
Thời gian cao
t
h
=
ln
(
2
)
⋅
(
R
1
+
R
2
)
⋅
C
{\displaystyle t_{h}=\ln(2)\cdot (R_{1}+R_{2})\cdot C}
Thời gian thấp
t
l
=
ln
(
2
)
⋅
R
2
⋅
C
{\displaystyle t_{l}=\ln(2)\cdot R_{2}\cdot C}
Năng xuất của R1 phải cao hơn giá trị của
V
c
c
2
R
1
{\displaystyle {\frac {V_{cc}^{2}}{R_{1}}}}
Mạch Điện
V
o
V
i
{\displaystyle {\frac {V_{o}}{V_{i}}}}
Chức năng
V
o
u
t
=
−
V
i
n
(
R
f
R
1
)
{\displaystyle V_{\mathrm {out} }=-V_{\mathrm {in} }\left({R_{f} \over R_{1}}\right)}
Khuếch Đại Điện Âm
V
o
u
t
=
V
i
n
(
1
+
R
2
R
1
)
{\displaystyle V_{\mathrm {out} }=V_{\mathrm {in} }\left(1+{R_{2} \over R_{1}}\right)}
V
o
u
t
=
V
i
n
{\displaystyle V_{\mathrm {out} }=V_{\mathrm {in} }\!\ }
V
o
u
t
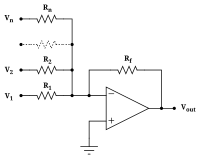
=
−
R
f
(
V
1
R
1
+
V
2
R
2
+
⋯
+
V
n
R
n
)
{\displaystyle V_{\mathrm {out} }=-R_{\mathrm {f} }\left({V_{1} \over R_{1}}+{V_{2} \over R_{2}}+\cdots +{V_{n} \over R_{n}}\right)}
V
o
u
t
=
∫
0
t
−
V
i
n
R
C
d
t
+
V
i
n
i
t
i
a
l
{\displaystyle V_{\mathrm {out} }=\int _{0}^{t}-{V_{\mathrm {in} } \over RC}\,dt+V_{\mathrm {initial} }}
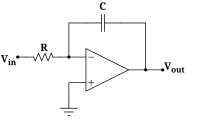
V
o
u
t
=
−
R
C
(
d
V
i
n
d
t
)
{\displaystyle V_{\mathrm {out} }=-RC\left({dV_{\mathrm {in} } \over dt}\right)}
−
R
1
R
2
V
s
a
t
{\displaystyle {\frac {-R_{1}}{R_{2}}}V_{sat}}
R
1
R
2
V
s
a
t
{\displaystyle {\frac {R_{1}}{R_{2}}}V_{sat}}
L RC
R
i
n
=
−
R
3
R
1
R
2
{\displaystyle R_{\mathrm {in} }=-R_{3}{\frac {R_{1}}{R_{2}}}}
v
o
u
t
=
−
V
γ
ln
(
v
i
n
I
S
⋅
R
)
{\displaystyle v_{\mathrm {out} }=-V_{\gamma }\ln \left({\frac {v_{\mathrm {in} }}{I_{\mathrm {S} }\cdot R}}\right)}
v
o
u
t
=
−
R
I
S
e
v
i
n
V
γ
{\displaystyle v_{\mathrm {out} }=-RI_{\mathrm {S} }e^{v_{\mathrm {in} } \over V_{\gamma }}}