Sách điện tử/Linh kiện điện tử/Cuộn từ

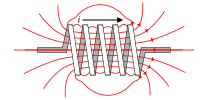
Cuộn Từ là một linh kiện điện tử có khả năng sanh từ trường khi mắc nối với điện .

Biểu Tượng mạch điện

Cuộn Từ có Biểu Tượng mạch điện

Từ dung

Tính chất

Từ Dung là tính chất vật lý của cuộn từ đại diện cho từ lượng sinh ra bởi một dòng điện trên cuộn từ . Từ Dung có ký hiệu mạch điện L đo bằng đơn vị Henry H . Từ dung của mọi vật dẩn điện dẩn điện đượ tính theo Định luật Ampere

$B={\frac {\mu }{A}}I=LI$

Từ đó, từ dung

$L={\frac {B}{I}}={\frac {\mu }{A}}$

Thí dụ

Cộng dây thẳng dẩn điện

$L={\frac {\mu }{2\pi r}}$

Vòng tròn dẩn điện

$L={\frac {\mu }{2r}}$

Cuộn tròn của N vòng tròn dẩn điện

$L=\mu {\frac {N}{l}}$

Phản ứng điện

Điện DC

Từ Cảm

$B=LI$

Từ Dung

$L={\frac {B}{I}}=N{\frac {\mu }{l}}$

Dòng Điện

$I={\frac {B}{L}}$

Điện AC

Điện Thế cuộn từ

$v(t)_{L}=\epsilon ={\frac {d}{dt}}\phi =L{\frac {d}{dt}}i(t)$

Dòng Điện

$i_{L}(t)={\frac {1}{L}}\int v(t)dt$

Điện Ứng

$X_{L}=\omega L\angle 90^{o}=j\omega L=sL$

Điện Kháng

$Z_{L}={\frac {v(t)}{i(t)}}=R_{L}+X_{L}$
$Z_{L}=R\angle 0+\omega L\angle 90=R+j\omega L=R+sL$

Góc Độ Khác Biệt Giửa Điện thế và Dòng Điện

$Tan\theta =\omega T=2\pi fT$

Hằng số thời gian

$T={\frac {L}{R}}$

Điện từ của cuộn từ

Điện từ cảm theo Định luật Ampere

$B=Li={\frac {N\mu _{o}}{l}}i$

Điện từ dung

$L={\frac {B}{i}}={\frac {N\mu _{o}}{l}}$

Điện lực

$F=Bl=N\mu _{o}i$

Điện từ thông nghịch theo Định luật Lenz

$-\phi =-NB=-NLi$

Điện từ cảm ứng nghịch theo Định luật Faraday

$-\epsilon ={\frac {d}{dt}}\phi =-NL{\frac {d}{dt}}i$

Điện từ thông thuận

$\phi =B=Li$

Điện từ cảm ứng thuận

$\epsilon ={\frac {d}{dt}}\phi =L{\frac {d}{dt}}i$

Điện nhiệt của cuộn từ

Nhiệt bên trong cuộn từ

Cuộn từ khi dẩn điện phát sinh ra nhiệt bên trong cuộn từ có năng lực nhiệt tính bằng

$W_{i}=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}$

Nhiệt tỏa vào môi trường xung quanh

Cuộn từ khi dẩn điện phát sinh ra nhiệt bên trong cuộn từ và sau một thời gian có khả năng giải thoát nhiệt vào môi trường xung quanh dưới dạng năng lượng nhiệt của Phóng xạ sóng điện từ

Tần số sóng điện từ

$\omega _{o}={\sqrt {\frac {1}{\mu _{o}\epsilon _{o}}}}=C=\lambda _{o}f_{o}$

Vận tốc di chuyển của sóng điện từ

$v=\omega _{o}$

Năng lực sóng điện từ

$W=pv=pC=p\lambda _{o}f_{o}=hf_{o}$

$h=p\lambda _{o}$

$p={\frac {h}{\lambda _{o}}}$

$\lambda _{o}={\frac {h}{p}}={\frac {C}{f_{o}}}$

Mạch điện cuộn từ

Mạch điện cuộn từ nối tiếp

$I=I_{1}+I_{2}+...I_{n}=V({\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+...{\frac {1}{L_{n}}})$

${\frac {I}{V}}={\frac {1}{L_{t}}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+...+{\frac {1}{L_{n}}}$

$V=IL_{t}$

Từ trên,

• Khi mắc nối tiếp nhiều cuôn từ lại với nhau, tổng từ dung sẻ tăng và bằng tổng của các từ dung

$L_{t}=L_{1}+L_{2}+...+L_{n}$

• Khi mắc nối tiếp n cuộn dây cùng giá trị từ dung, tổng từ dung sẻ tăng gấp n

$L_{t}=L_{1}+L_{2}+...+L_{n}=L+L+...+L=nL$

Mạch điện cuộn từ song song

$V=V_{1}+V_{2}+...V_{n}=IL_{1}+IL_{2}+...+IL_{n}=I(L_{1}+L_{2}+...+L_{n})$

$L_{t}={\frac {V}{I}}=(L_{1}+L_{2}+...+L_{n})$

$I={\frac {V}{L_{t}}}={\frac {V}{L_{1}+L_{2}+...+L_{n}}}$

Từ trên,

• Khi mắc nối tiếp nhiều cuôn từ lại với nhau, tổng từ dung sẻ tăng và bằng tổng của các từ dung

$L_{t}=L_{1}+L_{2}+...+L_{n}$

• Khi mắc nối tiếp n cuộn dây cùng giá trị từ dung, tổng từ dung sẻ tăng gấp n

$L_{t}=L_{1}+L_{2}+...+L_{n}=L+L+...+L=nL$