Sách toán ứng dụng kỹ sư

Vật

Tính chất vật lý và hóa học

Vật lượng

$M=\rho V$

Chất lượng

$\rho ={\frac {M}{V}}$

Thể tích vật chất

$V={\frac {M}{\rho }}$

Trạng thái vật chất

1. Rắn
2. Đặc
3. Lỏng
4. Khí

Thân nhiệt

1. Rắn - 0^oC
2. Đặc - 25^oC
3. Lỏng - 75^oC
4. Khí - 100^oC

Cấu tạo Vật

Vạt --> Nguyên chất --> Nguyên tố --> Nguyên tử

Mô hình nguyen tử vật chất

Mô hình Rutherford

Nguyen tử vật chất được tạo ra từ 2 mô hình

• Mô hình Rutherford cho rằng

Hạt nhân chứa điẹn tử dương và điện tử trung hòa ở trong tâm cùng với các vòng tròn quỹ đạo chứa điện tử âm quay quanh Hạt nhân

Lực

Lực cơ bản

Dạng lực	Công thức
Lực chuyển động	$F_{a}=ma$
Động lực	$F_{p}=m{\frac {v}{t}}={\frac {p}{t}}$
Trọng lực	$-F_{g}=mg=m{\frac {MG}{h^{2}}}$
Phản lực	$F_{-}=-F$
Áp lực	$F_{A}={\frac {F}{A}}$
Lực ma sát	$-F_{\mu }=\mu F_{N}$
Lực đàn hồi	$F_{x}=-kx$ $F_{y}=-ky$ $F_{\theta }=-l\theta$
Lực ly tâm	$F_{v}=m{\frac {v^{2}}{r}}=pvr$
Lực hướng tâm	$F_{r}=mvr=pr$
Lực Ampere	$F_{E}=QE$
Lực Coulomb	$F_{Q}=K{\frac {Q_{+}Q_{-}}{r^{2}}}$
Lực Lorentz	$F_{B}=\pm QvB$
Lực điện từ	$F_{EB}=F_{E}+F_{B}=Q(E\pm vB)$
Lực tương tác yếu
Lực tương tác mạnh

Lực và chuyển động

Các định luật về Chuyển động của Newton là một hệ thống gồm 3 định luật đặt nền móng cơ bản cho cơ học cổ điển.

F = 0	Không có lực tương tác , không có chuyển động	Vật sẽ đứng yên
F≠ 0	Lực tương tác với vật làm cho vật di chuyển tạo ra chuyển động	Vật sẽ di chuyển
Σ F = 0	Tổng lực trên vật bằng không, vật ở trạng thái cân bằng	Vật ở trạng thái cân bằng

Di chuyển tự do trên mặt phảng không bị cản trở

O →

$F_{p}=ma=m{\frac {v}{t}}={\frac {p}{t}}$

$p=mv=Ft$

$v={\frac {Ft}{m}}={\frac {p}{m}}$

$t={\frac {Ft}{m}}={\frac {p}{F_{p}}}$

Di chuyển tự do rơi xuống đất

O

↓

$-F_{g}=-mg=-{\frac {mMG}{h^{2}}}$

$-g=-{\frac {MG}{h^{2}}}$

$h={\sqrt {\frac {mMG}{g}}}$

Di chuyển điện tích theo đường thẳng ngang

$F_{Q}=QE=Q{\frac {V}{l}}={\frac {W}{l}}$

$W=QV=F_{Q}l$

$U={\frac {W}{t}}={\frac {QV}{t}}={\frac {F_{Q}l}{t}}=IV=F_{Q}v$

$E={\frac {F_{Q}}{Q}}={\frac {V}{l}}$

$l={\frac {W}{F_{Q}}}$

$v={\frac {l}{t}}={\frac {W}{F_{Q}t}}={\frac {U}{F_{Q}t}}$

$t={\frac {l}{v}}={\frac {W}{U}}$

Di chuyển điện tích theo đườn thẳng dọc

Chuyển động thẳng hàng của điện tích

$F_{B}=\pm QvB=QItB=QlB$

$W=F_{B}l=Ql^{2}B$

$U={\frac {W}{t}}={\frac {Ql^{2}B}{t}}$

$l={\frac {F_{B}}{IB}}$

$v={\frac {F_{B}}{QB}}$

$t={\frac {l}{v}}={\frac {Q}{I}}$

Di chuyển điện tích theo đường thẳng nghiêng

$F_{EB}=F_{E}+F_{B}=QE\pm QvB=Q(E\pm vB)$

$l\angle \theta ={\sqrt {l_{E}^{2}+l_{B}^{2}}}\angle tan^{-1}{\frac {l_{B}}{l_{E}}}$

$l_{E}={\frac {QV}{F_{E}}}$

$l_{B}={\frac {F_{B}}{IB}}$

Chuyển động lực hút điện tích khác loại

$F_{Q}=k{\frac {Q_{+}Q_{-}}{r^{2}}}=k{\frac {Q^{2}}{r^{2}}}$ Với $Q_{+}=Q_{-}$

$E={\frac {F_{Q}}{Q}}=k{\frac {Q}{r^{2}}}$

$W=\int Edr=k{\frac {Q}{r}}$

$U={\frac {W}{t}}=k{\frac {Q}{rt}}$

$r={\sqrt {k{\frac {Q^{2}}{F_{Q}}}}}$

Di chuyển trên mặt đất bị lực ma sát cản trở

$F_{p}=F_{\mu }$

$m{\frac {v}{t}}=\mu F_{N}$

$v={\frac {\mu F_{N}t}{m}}$

$v={\frac {mv}{\mu F_{N}}}$

$W_{\mu }=W_{p}$

$\mu F_{N}d=mgh$

$d={\frac {mgh}{\mu F_{N}}}$

$h={\frac {\mu F_{N}d}{mg}}$

Di chuyển tự do lơ lửng trên không trung

$F_{p}=F_{g}$

${\frac {mv}{t}}=mg$

$a=g={\frac {MG}{h^{2}}}$

$h={\sqrt {\frac {MG}{a}}}$

$v=gt$

$t={\frac {v}{g}}$

$W_{p}=W_{g}$

${\frac {mv^{2}}{2}}=mgh$

$v={\sqrt {2gh}}$

$d={\frac {v^{2}}{2g}}$

Di chuyển theo vòng tròn lơ lửng trong không trung

$F_{r}=F_{g}$

$mvr=mg$

$v={\frac {g}{r}}$

$r={\frac {g}{v}}$

$W_{r}=W_{g}$

${\frac {mv^{2}}{r}}=mgh$

$v={\sqrt {rgh}}$

$h={\frac {v^{2}}{rg}}$

Di chuyển theo hình cong rơi xuống đất với lực cản trở của không khí

${\vec {F}}={\vec {F}}_{p}+{\vec {F}}_{g}=F_{p}{\vec {i}}+F_{g}{\vec {j}}$

$F\angle \theta ={\sqrt {F_{p}^{2}+F_{g}^{2}}}\angle Tan^{-1}{\frac {F_{g}}{F_{p}}}$

$F_{p}=m{\frac {v}{t}}=Fcos\theta$

$F_{g}=mg=Fsin\theta$

$F={\frac {F_{p}}{cos\theta }}=F_{p}sec\theta =m{\frac {v}{t}}sec\theta$

$F={\frac {F_{g}}{sin\theta }}=F_{g}csc\theta =mgcsc\theta$

$\theta =cos^{-1}{\frac {F_{p}}{F}}=cos^{-1}{\frac {m{\frac {v}{t}}}{F}}$

$\theta =sin^{-1}{\frac {F_{g}}{F}}=cos^{-1}{\frac {mg}{F}}$

Di chuyển điện tích theo vòng tròn từ

$F_{B}=F_{r}$

$QvB=m{\frac {v^{2}}{r}}$

$v={\frac {Q}{m}}Br$

$r={\frac {mv^{2}}{QB}}$

Di chuyển sóng dợn từ dao động đàn hồi của Lò xo

Theo chiều ngang

$F_{a}=-F_{x}(t)$

$ma=-kx(t)$

$a=-\beta x(t)={\frac {d^{2}}{dt^{2}}}x(t)$

$x(t)=Ae^{st}=Ae^{\pm j\omega t}=Asin\omega t$

Với

$\omega ={\sqrt {\beta }}=\lambda f$

$\beta =-{\frac {k}{m}}$

Theo chiều dọc

$-F_{g}=F_{y}$

$-mg=-ky(t)$

$g=-\beta y(t)={\frac {d^{2}}{dt^{2}}}y(t)$

$y(t)=Ae^{st}=Ae^{\pm j\omega t}=Asin\omega t$

Với

$\omega ={\sqrt {\beta }}=\lambda f$

$\beta =-{\frac {k}{m}}$

Di chuyển sóng dợn từ dao động đong đưa của Con lắc đồng hồ

$-F_{g}=F_{\theta }$

$-mg=-k\theta (t)$

$g=-\beta \theta (t)={\frac {d^{2}}{dt^{2}}}theta(t)$

$\theta (t)=Ae^{st}=Ae^{\pm j\omega t}=Asin\omega t$

Với

$\omega ={\sqrt {\beta }}=\lambda f$

$\beta =-{\frac {l}{m}}$

Chuyển động

Dạng chuyển động

Động lượng

v < C

$v=v$

$a={\frac {v}{t}}$

$s=vt$

$F=ma=m{\frac {v}{t}}={\frac {p}{t}}$

$W=Fs={\frac {P}{t}}s=pv$

$E={\frac {W}{t}}={\frac {pv}{t}}=pa$

$p=mv=Ft$

$m={\frac {p}{v}}={\frac {Ft}{v}}$

v = C

$v=C=\lambda f$

$a={\frac {C}{t}}$

$s=Ct$

$F={\frac {p}{t}}={\frac {\frac {h}{\lambda }}{t}}={\frac {hf}{\lambda }}$

$W=pv=p\omega =pC=p\lambda f=hf$

$E=pa={\frac {pC}{t}}=hf^{2}$

$p={\frac {h}{\lambda }}$

$\lambda ={\frac {h}{p}}$

$h=p\lambda$

v ≈ C

$v=C=\beta$

$a={\frac {C}{t}}\beta$

$s=Ct\beta$

$F={\frac {p}{t}}\beta$

$W=pv\beta$

$E=pa\beta$

$p={\frac {p_{o}}{\gamma }}$

$p_{o}=p\gamma$

Di chuyển theo đường thẳng nghiêng

$a={\frac {\Delta v}{\Delta t}}={\frac {v-v_{o}}{t-t_{o}}}$

$v=v_{o}+a\Delta t$

$s=\Delta t(v_{o}+{\frac {\Delta v}{2}})=\Delta t(v_{o}+{\frac {a\Delta t}{2}})=\Delta t(v-{\frac {a\Delta t}{2}})={\frac {v^{2}-v_{o}^{2}}{2a}}$

$F=ma=m{\frac {\Delta v}{\Delta t}}=m{\frac {v-v_{o}}{t-t_{o}}}$

$W=Fs=F\Delta t(v_{o}+{\frac {at^{2}}{2}})$

$E={\frac {W}{t}}=F(v_{o}+{\frac {at^{2}}{2}})$

Di chuyển theo đường cong

$v=v(t)$

$a={\frac {d}{\Delta t}}v(t)$

$s=\int v(t)dt$

$F=ma=m{\frac {d}{\Delta t}}v(t)$

$W=Fs=F\int v(t)dt$

$E={\frac {W}{t}}={\frac {F}{t}}\int v(t)dt$

$s=s(t)$

$v={\frac {d}{\Delta t}}s(t)$

$a={\frac {d^{2}}{\Delta t^{2}}}s(t)$

$F=ma=m{\frac {d^{2}}{\Delta t^{2}}}s(t)$

$W=Fs=Fvt=pv=p{\frac {d}{\Delta t}}s(t)$

$E={\frac {W}{t}}={\frac {pv}{t}}=pa=p{\frac {d^{2}}{\Delta dt^{2}}}s(t)$

Di chuyển theo vòng tròn

$s=2\pi$

$v={\frac {s}{t}}={\frac {2\pi }{t}}=2\pi f=\omega$

$a={\frac {v}{t}}={\frac {\omega }{t}}$

$F=ma==m{\frac {\omega }{t}}$

$W=Fs=Fvt=pv=p\omega$

$E={\frac {W}{t}}={\frac {pv}{t}}=pa=p{\frac {\omega }{t}}$

Di chuyển theo cung tròn

$s=r\theta$

$v=r\omega$

$a=r\alpha$

$F=ma=mr\alpha$

$W=Fs=Fvt=pv=pr\omega$

$E={\frac {W}{t}}={\frac {pv}{t}}=pa=pr{\frac {\omega }{t}}$

Với

$\alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\omega -\omega _{o}}{t-t_{o}}}$

$\omega =\omega _{o}+\alpha \Delta t$

$\theta =\Delta t(\omega _{o}+{\frac {\Delta \omega }{2}})$

Di chuyển theo sóng sin

$s=k\lambda$

$v={\frac {s}{t}}={\frac {k\lambda }{t}}=k\lambda f=k\omega$

$a={\frac {v}{t}}={\frac {k\omega }{t}}$

$F=ma={\frac {k\omega }{t}}$

$W=Fs=Fvt=pv=pk\omega$

$E={\frac {W}{t}}={\frac {pv}{t}}=pa=p{\frac {k\omega }{t}}$

$k={\frac {s}{\lambda }}={\frac {v}{\omega }}$

$\omega =\lambda f={\frac {\lambda }{t}}={\frac {v}{k}}$

$\lambda ={\frac {\omega }{f}}=\omega t={\frac {s}{k}}$

$f={\frac {\omega }{\lambda }}={\frac {1}{t}}$

$t={\frac {\omega }{\lambda }}={\frac {1}{f}}$

Vector chuyển động

Chuyển động định hướng là một loại chuyển động theo một hướng cố định . Chuyển động định hướng được biểu diển bằng vector chuyển động như sau

${\vec {A}}=A{\vec {a}}$

'Vector chuyển động	Công thức toán
Vector chuyển động theo đường thẳng ngang	${\vec {X}}=X{\vec {i}}$
Vector chuyển động theo đường thẳng dọc	${\vec {Y}}=Y{\vec {j}}$
Vector chuyển động theo đường thẳng nghiêng	${\vec {Z}}=Z{\vec {k}}$
Vector chuyển động theo đường tròn	${\vec {R}}=R{\vec {r}}={\vec {Z}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}$

Bán kín Bohr

$Q_{e}=e$

$Q_{pn}=Ze$

$F_{Q}=F_{r}$

$k{\frac {Ze^{2}}{r^{2}}}={\frac {mv^{2}}{r}}$

$r={\frac {kZe^{2}}{mv^{2}}}$

$p_{h}=p_{r}$

$nh=2\pi mvr$

$v={\frac {n\hbar }{mr}}$

$r={\frac {kZe^{2}}{m({\frac {n\hbar }{mr}})^{2}}}$

Cân bàng năng lượng

$E=E_{p}+E=0$

Vạch sáng

$\Delta E=E_{n}-E_{n-1}=nhf=nh{\frac {C}{\lambda }}$

$f={\frac {\Delta E}{nh}}$

${\frac {1}{\lambda }}={\frac {\Delta E}{nhC}}$

Lượng tử sáng của điện tử đi ra khỏ nguyên tử

$hf=hf_{o}+{\frac {1}{2}}mv^{2}$

$h={\frac {mv^{2}}{2\Delta f}}$

$v={\sqrt {\frac {2h\Delta f}{m}}}$

Lượng tử tối đi vô trong nguyên tử

$nhf=mvr2\pi$

$\hbar ={\frac {h}{2\pi }}={\frac {mvr}{nf}}$

$v={\frac {nf\hbar }{mr}}$

Điện

Điện nguồn

Điện DC được tạo ra từ các nguồn phát điện sau

• Điện giải

$v(t)=V$ || Bình ắc quy

• Điện cực

|| $v(t)=V$ || Pin cục

• Quang tuyến nhiệt điện

|| $v(t)=V$ || Pin mặt trời

• Biến điện AC ra điện DC

||
$v(t)=V$

Điện loại

Điện DC

Điện nguồn

Nguồn điện	Hình	Công thức	Ứng dụng
Điện giải		$v(t)=V$	Bình ắc quy
Điện cực		$v(t)=V$	Pin cục
Quang tuyến nhiệt điện		$v(t)=V$	Pin mặt trời
Biến điện AC ra điện DC		$v(t)=V$

Tính chất

Ký hiệu

Công thức toán

$v(t)=V$

Tính toán điện DC

$I={\frac {Q}{t}}$

$Q=It$

$V={\frac {W}{Q}}$

$W=QV$

$E={\frac {W}{t}}={\frac {QV}{t}}=IV$

Điện AC

Điện nguồn

Tính chất

Ký hiệu

Công thức toán

$v(t)=Vsin\omega t$

Tính toán điện AC

$i(t)={\frac {d}{dt}}Q(t)$

$Q(t)=\int i(t)dt$

$v(t)={\frac {dW(t)}{Q(t)dt}}$

$W(t)=\int v(t)dQ(t)=\int v(t)i(t)dt=\int p(t)dt$

$E(t)={\frac {d}{dt}}W(t)={\frac {d}{dt}}p(t)dt$

Định luật điện

Định luật Vôn	$V=IR$
Định luật Ampe	$V=IR$
Định luật Wat	$P=IV=I^{2}R={\frac {V^{2}}{R}}$
Định luật Ôm	$R={\frac {V}{I}}$

Điện từ

Điện từ là một hiện tượng của mọi vật dẩn điện mắc nối với điện tạo ra từ trường có khả năng hút các kim loại nằm kề bên khi có dòng điện đi qua vật dẩn điện nên được gọi là Nam châm điện

Nam châm điện

Nam châm điện thường

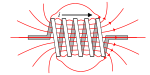
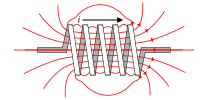
Thí nghiệm cho thấy, Nam châm điện thường được tạo ra từ mắc nối các dẩn điện như Cộng dây thẳng dẩn điện, Vòng tròn dẩn điện và Cuộn tròn dẩn điện với điện

Nam châm điện thường tạo ra từ các lối mắc trên đều có các tính chất sau

• Từ sinh khi Nam châm điện thường dẩn điện

I ≠ 0 . B ≠ 0 = LI

• Từ biến mất khi Nam châm điện thường không dẩn điện

I = 0 . B = 0

Nam châm điện vĩnh cửu

Thí nghiệm cho thấy, Nam châm điện vĩnh cửu được tạo ra bằng cách để một từ vật nằm trong các vòng tròn của cuộn tròn dẩn điện mắc nối với điện

Nam châm điện vỉnh cửu tạo ra từ lối mắc trên có các tính chất sau

• Từ sinh khi Nam châm điện thường dẩn điện

I ≠ 0 . B ≠ 0 . H ≠ 0

• Từ biến mất khi Nam châm điện thường không dẩn điện

I = 0 . B = 0 . H ≠ 0

Định luật Điện từ trường

Định luật Điện từ trường	Ý nghỉa	Công thức
Định luật Gauss	Mật độ điện trường và từ trường trong một diện tích	$\Phi _{E}=\oint _{S}\mathbf {E} \cdot d\mathbf {A} ={1 \over \epsilon _{o}}\int _{V}\rho \ dV={\frac {Q_{A}}{\epsilon _{o}}}$ $\Phi _{B}=\oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }$
Định luật Ampere	Từ cảm của cuộn từ dẩn điện	$B=Li={\frac {\mu }{A}}i$
Định luật Lentz	Từ cảm ứng của cuộn từ dẩn điện	$-\phi =-NB=-NLi$
Định luật Faraday	Điện từ cảm ứng của cuộn từ dẩn điện	$-\epsilon =-\int Edl=-{\frac {d\phi _{B}}{dt}}=-NL{\frac {di}{dt}}$
Định luật Maxwell	Từ nhiểm của cuộn từ dẩn điện	$H={\frac {B}{\mu }}$
Định luật Maxwell-Ampere	Dòng điện	$i=\oint _{C}\mathbf {H} \cdot \mathrm {d} \mathbf {l} =\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {A} +{\mathrm {d} \over \mathrm {d} t}\iint _{S}\mathbf {D} \cdot \mathrm {d} \mathbf {A}$ $\oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }+{\frac {d\mathbf {\Phi _{E}} }{dt}}$

Điện tích

Cường độ Điện lượng, Điện trường, Từ trường

$EA={\frac {Q}{\epsilon }}$

$BA=\mu I$

$Q=\epsilon EA=DA$

$I={\frac {BA}{\mu }}=HA$

$E={\frac {Q}{\epsilon A}}={\frac {D}{\epsilon }}$

$B={\frac {\mu I}{A}}=\mu H$

Tính chất

Vật tích điện bằng cách cho hay nhận điện tử âm trở thành điện tích dương hay điện tích âm . Mọi điện tích dương hay điện tích âm đều có các tính chất sau

Điện tích	Ký hiệu	Tích điện	Điện lượng	Điện trường	Từ trường
Điện tích âm	(-)	Vật + e	-Q	→E←	B
Điện tích dương	(+)	Vật - e	+Q	←E↔	B

Tương tác Điện tích

Tương tác giửa điện tích với điện tích , với điện trường , với từ trường tạo ra các lực tương tác điện tích sau

Lực tương tác điện tích	Hình	Công thức lực tương tác
Lực điện động	→ O → O	$F=QE$
Lực từ đông		$F=\pm QvB$
Lực điện từ		$F=Q(E\pm vB)$
Lực hút điện tích		$F=K{\frac {Q_{+}Q_{-}}{r^{2}}}$

Lực động điện

Lực động điện làm cho điện tích đứng yên di chuyển theo đường thẳng ngang . Di chuyển của điện tích có các tính chất sau

$F_{E}=QE=Q{\frac {V}{l}}={\frac {W}{l}}$

$W_{E}=QV=F_{E}l$

$F_{E}={\frac {W_{E}}{t}}={\frac {QV}{t}}=VI={\frac {F_{E}l}{t}}=F_{E}v$

$l={\frac {W}{F}}$

$v={\frac {l}{t}}={\frac {W}{lt}}={\frac {U}{l}}$

$t={\frac {l}{v}}={\frac {W}{U}}$

Lực động từ

Lực động từ làm cho điện tích đứng yên di chuyển theo đường thẳng dọc . Di chuyển của điện tích có các tính chất sau

Di chuyển điện tích theo đường thẳng không đổi

$F_{B}=QvB=ItvB=IBl$

$W_{B}=F_{B}l=IBl^{2}$

$E_{B}={\frac {W_{E}}{t}}={\frac {IBl^{2}}{t}}=IBlv=F_{B}v$

$l={\frac {F}{IB}}$

$v={\frac {F}{QB}}$

$t={\frac {l}{v}}={\frac {Q}{I}}$

Di chuyển điện tích theo quỹ đạo vòng tròn

$F_{B}=F_{p}$

$QvB=m{\frac {v^{2}}{r}}$

$v={\frac {Q}{m}}Br$

$r={\frac {mv^{2}}{Qv}}$

Lực điện từ

Lực điện từ làm cho điện tích đứng yên di chuyển theo đường thẳng nghiêng. Di chuyển của điện tích có các tính chất sau

${\vec {F}}_{EB}={\vec {F}}_{E}+{\vec {F}}_{B}=F_{E}{\vec {i}}+F_{B}{\vec {j}}=Q({\vec {E}}\pm v{\vec {B}})$

Từ trên

• Khi, $v=0$

${\vec {F}}_{EB}=QE$ .

• Khi, $E=0$

${\vec {F}}_{EB}=QvB$ .

• Khi, $E\pm vB=0$

${\vec {F}}_{EB}=0$

$E=vB$

$B={\frac {1}{v}}E$

$v={\frac {E}{B}}$

Lực hút điện tích

Lực hút của điện tích âm hút điện tích dương về hướng mình tạo ra chuyển động có các tính chất sau

$F_{Q}=K{\frac {Q_{+}Q_{-}}{r^{2}}}$

Với $Q_{+}=Q_{-}$

$F_{Q}=K{\frac {Q^{2}}{r^{2}}}$

$r={\sqrt {\frac {KQ^{2}}{F_{Q}}}}$

Điện từ và dẩn điện

Cộng dây thẳng dẩn điện

$B=Li={\frac {\mu }{2\pi r}}i$

$i={\frac {B}{L}}={\frac {\mu }{2\pi r}}$

Vòng tròn dẩn điện

$B=Li={\frac {\mu }{2\pi }}i$

$i={\frac {B}{L}}={\frac {\mu }{2\pi }}$

$\phi =B=Li$

N Vòng tròn dẩn điện

H ≠ 0

$B=Li={\frac {N\mu }{l}}i$

$i={\frac {B}{L}}={\frac {N\mu }{l}}$

$\phi =B=Li$

$\epsilon ={\frac {d}{dt}}\phi =L{\frac {d}{dt}}i$

$-\phi =-NB=-NLi$

$-\epsilon =-{\frac {d}{dt}}\phi =-NL{\frac {d}{dt}}i$

$H={\frac {B}{\mu }}$

$F=Bl=N\mu i$

H = 0

$B=Li={\frac {N\mu }{l}}i$

$i={\frac {B}{L}}={\frac {N\mu }{l}}$

$\phi =B=Li$

$\epsilon ={\frac {d}{dt}}\phi =L{\frac {d}{dt}}i$

$-\phi =-NB=-NLi$

$-\epsilon =-{\frac {d}{dt}}\phi =-NL{\frac {d}{dt}}i$

$F=Bl=N\mu i$

Sóng điện từ

Trong môi trường vật chất , H≠0

Phương trình vector dao động điện từ

Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T}}B$
$T=\mu \epsilon$

Phương trình và hàm sóng điện từ

Cho một Phương trình sóng điện từ

$\nabla ^{2}E=-\beta E$

$\nabla ^{2}B=-\beta B$

$\beta ={\sqrt {\frac {1}{T}}}$

Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ

$E=ASin\omega t$

$B=ASin\omega t$

$\omega =\lambda f={\sqrt {\frac {1}{T}}}=C$

$T=\mu \epsilon$

Trong môi trường chân không , H=0

Phương trình vector dao động điện từ

Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B

$\nabla \cdot E=0$
$\nabla \times E=-{\frac {1}{T_{o}}}E$
$\nabla \cdot B=0$
$\nabla \times B=-{\frac {1}{T_{o}}}B$
$T_{o}=\mu _{o}\epsilon _{o}$

Phương trình và hàm sóng điện từ

Cho một Phương trình sóng điện từ

$\nabla ^{2}E=-\beta _{o}E$

$\nabla ^{2}B=-\beta _{o}B$

$\omega _{o}={\sqrt {\frac {1}{T_{o}}}}$

Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ

$E=ASin\omega _{o}t$

$B=ASin\omega _{o}t$

$\omega _{o}=\lambda _{o}f_{o}={\sqrt {\frac {1}{T_{o}}}}=C$

$T_{o}=\mu _{o}\epsilon _{o}$

Nhiệt điện từ, hiện tượng nhiệt tìm thấy từ các mạch điện tạo ra từ trường của cộng dây thẳng dẫn điện và cuộn từ dẫn điện

Nhiệt điện từ

≈≈≈ || ≈≈≈==|| ≈≈≈e

Nhiệt điện từ	Nhiệt	Nhiệt quang	Nhiệt điện
Lối mắc	Cộng dây thẳng dẫn điện	Cuộn tròn của N vòng tròn dẫn điện	Cuộn tròn của N vòng tròn dẫn điện với từ vật nằm trong các vòng quấn
Tần số thời gian	$f<f_{o}$	$f=f_{o}$	$f>f_{o}$
Năng lực nhiệt	$W=pv=mC\Delta T$	$W_{o}=pv=pC=hf_{o}$	$W=pv=pC=hf$
Hằng số C	$C=p{\frac {v}{m\Delta T}}$	$C={\sqrt {\frac {1}{\mu _{o}\epsilon _{o}}}}=\omega _{o}=\lambda _{o}f_{o}$	$C={\sqrt {\frac {1}{\mu \epsilon }}}=\omega =\lambda f$
Khối lượng/Lượng tử	$m=p\lambda =p{\frac {C\Delta T}{v}}$	$h=p\lambda _{o}$	$h=p\lambda$
Động lượng	$p={\frac {m}{\lambda }}=m{\frac {v}{C\Delta T}}$	$p={\frac {h}{\lambda _{o}}}$	$p={\frac {h}{\lambda }}$
Bước sóng	$\lambda ={\frac {m}{p}}={\frac {C\Delta T}{v}}$	$\lambda _{o}={\frac {C}{f_{o}}}={\frac {h}{p}}$	$\lambda ={\frac {C}{f}}={\frac {h}{p}}$