Hàm số là một biểu thức đại số được dùng trong việc biểu diển tương quan giửa 2 đại lương với nhau . Thí dụ như
y
=
2
x
+
5
{\displaystyle y=2x+5}
Mọi hàm số đều có một hay nhiều hơn một biến số
Mọi hàm số của một biến số
f
(
x
)
{\displaystyle f(x)}
y
=
2
x
{\displaystyle y=2x}
Hàm số 2 biến số
f
(
x
,
y
)
{\displaystyle f(x,y)}
r
2
=
x
2
+
y
2
{\displaystyle r^{2}=x^{2}+y^{2}}
f
(
r
,
θ
)
{\displaystyle f(r,\theta )}
Z
∠
θ
=
(
x
2
+
y
2
)
∠
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {(}}x^{2}+y^{2})\angle tan^{-1}{\frac {y}{x}}}
Hàm số 3 biến số
f
(
x
,
y
,
z
)
{\displaystyle f(x,y,z)}
r
2
=
x
2
+
y
2
+
z
2
{\displaystyle r^{2}=x^{2}+y^{2}+z^{2}}
Hàm số bằng không
f
(
x
)
=
0
{\displaystyle f(x)=0}
Hàm số bằng hằng số không đổi
f
(
x
)
=
C
{\displaystyle f(x)=C}
Hàm số khác không
f
(
x
)
=
y
(
x
)
{\displaystyle f(x)=y(x)}
Dạng hàm số Công thức Thí dụ
Hàm số tuần hoàn (Periodic function)
f
(
x
)
=
f
(
x
+
T
)
{\displaystyle f(x)=f(x+T)}
s
i
n
x
=
s
i
n
(
x
+
k
2
π
)
{\displaystyle sinx=sin(x+k2\pi )}
Hàm số chẳn (Even function)
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
Hàm số lẽ (Odd function)
f
(
x
)
=
−
f
(
x
)
{\displaystyle f(x)=-f(x)}
y
(
x
)
=
−
y
(
x
)
{\displaystyle y(x)=-y(x)}
Hàm số nghịch đảo (Inverse function)
f
−
1
(
x
)
=
1
f
(
x
)
{\displaystyle f^{-1}(x)={\frac {1}{f(x)}}}
s
i
n
−
1
x
=
1
s
i
n
x
{\displaystyle sin^{-1}{x}={\frac {1}{sinx}}}
Hàm số trong hàm số (Composite function)
f
(
x
)
=
f
(
g
(
x
)
)
{\displaystyle f(x)=f(g(x))}
Hàm số nhiều biến số (Parametric function)
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Hàm số tương quan/]] (Recursive function)
Hàm số chia/]] (Rational function)
Q
(
x
)
=
N
(
x
)
M
(
x
)
−
R
(
x
)
{\displaystyle Q(x)={\frac {N(x)}{M(x)}}-R(x)}
[ sửa ]
Dạng hàm số Công thức Thí dụ
y
=
y
o
+
Z
(
x
−
x
o
)
{\displaystyle y=y_{o}+Z(x-x_{o})}
y
=
a
x
+
b
{\displaystyle y=ax+b}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
(
Z
Z
)
2
=
(
X
Z
)
2
+
(
Y
Z
)
2
{\displaystyle ({\frac {Z}{Z}})^{2}=({\frac {X}{Z}})^{2}+({\frac {Y}{Z}})^{2}}
1
=
c
o
s
2
+
s
i
n
2
{\displaystyle 1=cos^{2}+sin^{2}}
1
=
s
e
c
2
+
t
a
n
2
{\displaystyle 1=sec^{2}+tan^{2}}
1
=
c
s
c
2
+
c
o
t
2
{\displaystyle 1=csc^{2}+cot^{2}}
y
=
a
x
n
{\displaystyle y=ax^{n}}
y
(
x
)
=
L
o
g
x
{\displaystyle y(x)=Logx}
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
s
e
c
θ
=
1
X
{\displaystyle sec\theta ={\frac {1}{X}}}
c
s
c
θ
=
1
Y
{\displaystyle csc\theta ={\frac {1}{Y}}}
t
a
n
θ
=
Y
X
{\displaystyle tan\theta ={\frac {Y}{X}}}
c
o
t
θ
=
X
Y
{\displaystyle cot\theta ={\frac {X}{Y}}}
[ sửa ] Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
+
.
.
.
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
+
.
.
.
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}+...=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}+...}
Chứng minh Khi x=0
f
(
0
)
=
a
0
{\displaystyle f(0)=a_{0}}
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
f
′
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
4
a
4
x
3
{\displaystyle f^{'}(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+4a_{4}x^{3}}
f
′
(
0
)
=
a
1
{\displaystyle f^{'}(0)=a_{1}}
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
f
″
(
x
)
=
2
a
2
+
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
a
4
x
2
+
(
5
)
(
4
)
a
5
x
3
{\displaystyle f^{''}(x)=2a_{2}+(3)(2)a_{3}x+(4)(3)a_{4}x^{2}+(5)(4)a_{5}x^{3}}
f
″
(
0
)
=
2
a
2
{\displaystyle f^{''}(0)=2a_{2}}
a
2
=
f
″
(
0
)
2
{\displaystyle a_{2}={\frac {f^{''}(0)}{2}}}
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
f
‴
(
x
)
=
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
(
2
)
a
4
x
+
(
5
)
(
4
)
(
3
)
a
5
x
2
{\displaystyle f^{'''}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_{5}x^{2}}
f
‴
(
0
)
=
(
3
)
(
2
)
a
3
{\displaystyle f^{'''}(0)=(3)(2)a_{3}}
a
3
=
f
‴
(
0
)
3
!
{\displaystyle a_{3}={\frac {f^{'''}(0)}{3!}}}
Thế
a
0
,
a
−
1
,
a
−
2
{\displaystyle a_{0},a-1,a-2}
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}}
f
(
x
)
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
{\displaystyle f(x)=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}}
Thí dụ
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f(0)=\sin(0)=0}
f
″
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{''}(x)=-\sin(x)}
f
″
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{''}(0)=-\sin(0)=0}
f
‴
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{'''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
sin
(
x
)
=
0
+
x
(
1
)
+
x
2
2
!
(
0
)
+
x
3
3
!
(
−
1
)
+
x
5
5
!
(
1
)
=
x
−
x
3
3
!
+
x
5
5
!
{\displaystyle \sin(x)=0+x(1)+{\frac {x^{2}}{2!}}(0)+{\frac {x^{3}}{3!}}(-1)+{\frac {x^{5}}{5!}}(1)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
0
)
=
cos
(
0
)
=
1
{\displaystyle f(0)=\cos(0)=1}
f
′
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{'}(x)=-\sin(x)}
f
′
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{'}(0)=-\sin(0)=0}
f
″
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
f
‴
(
x
)
=
sin
(
x
)
{\displaystyle f^{'''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
cos
(
x
)
=
1
+
x
(
0
)
+
x
2
2
!
(
−
1
)
+
x
3
3
!
(
0
)
+
x
4
4
!
(
1
)
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
{\displaystyle \cos(x)=1+x(0)+{\frac {x^{2}}{2!}}(-1)+{\frac {x^{3}}{3!}}(0)+{\frac {x^{4}}{4!}}(1)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}}
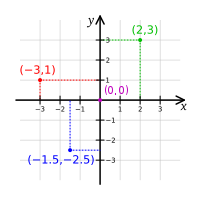
Đồ Thị là một cách hiển thị Tọa độ của một điểm trên một mặt phẳng . Có hai loại đồ thị Đồ Thị điểm XY và Đồ Thị điểm Rθ
Tương quan giửa 2 đại lượng x, y biểu thị bằng hàm sô
y
=
x
{\displaystyle y=x}
Lập bảng tương quan giửa hai giá trị x và y
x -2
-1
0
1
2
y = x -2
-1
0
1
2
Đặt điểm (x,y) trên đồ thi x-y ta có Đồ thị hàm số đường thẳng đi qua điểm gốc (0,0) có độ nghiêng bằng 1
Đồ thị của các hàm số cơ bản
Dạng hàm số Công thức Đồ thị
Hàm số đường thẳng
Hàm số đường thẳng qua 2 điểm bất kỳ
y
=
y
o
+
a
(
x
−
x
o
)
{\displaystyle y=y_{o}+a(x-x_{o})}
y
=
a
x
+
b
{\displaystyle y=ax+b}
x
o
=
0
,
y
o
=
b
{\displaystyle x_{o}=0,y_{o}=b}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
Z
Z
2
=
X
Z
2
+
Y
Z
2
{\displaystyle {\frac {Z}{Z}}^{2}={\frac {X}{Z}}^{2}+{\frac {Y}{Z}}^{2}}
1
=
c
o
s
2
+
s
i
n
2
{\displaystyle 1=cos^{2}+sin^{2}}
1
=
s
e
c
2
+
t
a
n
2
{\displaystyle 1=sec^{2}+tan^{2}}
1
=
c
s
c
2
+
c
o
t
2
{\displaystyle 1=csc^{2}+cot^{2}}
y
=
a
x
n
{\displaystyle y=ax^{n}}
y
(
x
)
=
L
o
g
x
{\displaystyle y(x)=Logx}
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
c
o
s
θ
=
Y
Z
{\displaystyle cos\theta ={\frac {Y}{Z}}}
c
o
s
θ
=
1
X
{\displaystyle cos\theta ={\frac {1}{X}}}
c
o
s
θ
=
1
Y
{\displaystyle cos\theta ={\frac {1}{Y}}}
c
o
s
θ
=
Y
X
{\displaystyle cos\theta ={\frac {Y}{X}}}
c
o
s
θ
=
X
Y
{\displaystyle cos\theta ={\frac {X}{Y}}}
Radial lines (those running through the pole) are represented by the equation
φ
=
γ
,
{\displaystyle \varphi =\gamma ,}
γ
{\displaystyle \gamma }
φ
=
arctan
m
{\displaystyle \varphi =\arctan m}
m
{\displaystyle m}
slope of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line
φ
=
γ
{\displaystyle \varphi =\gamma }
perpendicularly at the point
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
r
(
φ
)
=
r
0
sec
(
φ
−
γ
)
.
{\displaystyle r(\varphi )=r_{0}\sec(\varphi -\gamma ).}
Otherwise stated
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
r
0
{\displaystyle r_{0}}
A circle with equation r (φ ) = 1 The general equation for a circle with a center at
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
a is
r
2
−
2
r
r
0
cos
(
φ
−
γ
)
+
r
0
2
=
a
2
.
{\displaystyle r^{2}-2rr_{0}\cos(\varphi -\gamma )+r_{0}^{2}=a^{2}.}
This can be simplified in various ways, to conform to more specific cases, such as the equation
r
(
φ
)
=
a
{\displaystyle r(\varphi )=a}
a .
When r 0 = a
r
=
2
a
cos
(
φ
−
γ
)
.
{\displaystyle r=2a\cos(\varphi -\gamma ).}
In the general case, the equation can be solved for r
r
=
r
0
cos
(
φ
−
γ
)
+
a
2
−
r
0
2
sin
2
(
φ
−
γ
)
{\displaystyle r=r_{0}\cos(\varphi -\gamma )+{\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\varphi -\gamma )}}}
A polar rose with equation r (φ ) = 2 sin 4φ A polar rose is a mathematical curve that looks like a petaled flower, and that can be expressed as a simple polar equation,
r
(
φ
)
=
a
cos
(
k
φ
+
γ
0
)
{\displaystyle r(\varphi )=a\cos \left(k\varphi +\gamma _{0}\right)}
for any constant γ0 (including 0). If k is an integer, these equations will produce a k -petaled rose if k is odd , or a 2k -petaled rose if k is even. If k is rational, but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable a directly represents the length or amplitude of the petals of the rose, while k relates to their spatial frequency. The constant γ0 can be regarded as a phase angle.
One arm of an Archimedean spiral with equation r (φ ) = φ / 2π 0 < φ < 6π pi The Archimedean spiral is a spiral discovered by Archimedes which can also be expressed as a simple polar equation. It is represented by the equation
r
(
φ
)
=
a
+
b
φ
.
{\displaystyle r(\varphi )=a+b\varphi .}
a will turn the spiral, while b controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for φ > 0φ < 0a = 0conic sections , to be described in a mathematical treatise, and as a prime example of a curve best defined by a polar equation.
Ellipse, showing semi-latus rectum A conic section with one focus on the pole and the other somewhere on the 0° ray (so that the conic's major axis lies along the polar axis) is given by:
r
=
ℓ
1
−
e
cos
φ
{\displaystyle r={\ell \over {1-e\cos \varphi }}}
e is the eccentricity and
ℓ
{\displaystyle \ell }
semi-latus rectum (the perpendicular distance at a focus from the major axis to the curve). If e > 1hyperbola ; if e = 1parabola ; and if e < 1ellipse . The special case e = 0
ℓ
{\displaystyle \ell }
Intersection of two polar curves [ sửa ] The graphs of two polar functions
r
=
f
(
θ
)
{\displaystyle r=f(\theta )}
r
=
g
(
θ
)
{\displaystyle r=g(\theta )}
In the origin, if the equations
f
(
θ
)
=
0
{\displaystyle f(\theta )=0}
g
(
θ
)
=
0
{\displaystyle g(\theta )=0}
All the points
[
g
(
θ
i
)
,
θ
i
]
{\displaystyle [g(\theta _{i}),\theta _{i}]}
θ
i
{\displaystyle \theta _{i}}
f
(
θ
+
2
k
π
)
=
g
(
θ
)
{\displaystyle f(\theta +2k\pi )=g(\theta )}
k
{\displaystyle k}
All the points
[
g
(
θ
i
)
,
θ
i
]
{\displaystyle [g(\theta _{i}),\theta _{i}]}
θ
i
{\displaystyle \theta _{i}}
f
(
θ
+
(
2
k
+
1
)
π
)
=
−
g
(
θ
)
{\displaystyle f(\theta +(2k+1)\pi )=-g(\theta )}
k
{\displaystyle k}
Thay đổi biến số x
Δ
x
=
(
x
+
Δ
x
)
−
x
{\displaystyle \Delta x=(x+\Delta x)-x}
Thay đổi biến số y
Δ
y
=
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=\Delta f(x)=f(x+\Delta x)-f(x)}
Biến đổi hàm số tính bằng tỉ lệ thay đổi biến số y trên thay đổi biến số x
Δ
y
Δ
x
=
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}}
Phép toán giải tích tìm biến đổi của một hàm số toán
Đạo hàm
d
d
x
f
(
x
)
=
f
′
(
x
)
=
lim
Δ
x
→
0
∑
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
∑
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=f^{'}(x)=\lim _{\Delta x\to 0}\sum {\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}\sum {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
Phép toán giải tích tìm tổng biến đổi của một hàm số toán
Loại tích phân Hình Công thức
Tích phân xác định
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)}
Tích phân bất định
∫
f
(
x
)
d
x
=
lim
Δ
x
→
0
∑
(
f
(
x
)
+
Δ
f
(
x
)
2
)
Δ
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)dx=\lim _{\Delta x\rightarrow 0}\sum (f(x)+{\frac {\Delta f(x)}{2}})\Delta x=F(x)+C}




















































































































![{\displaystyle [g(\theta _{i}),\theta _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3942e962cea54fd104a33ebac17dde8bffa819)










