[ sửa ]
Name
Usual notation
Definition
Domain of
x
{\displaystyle x}
Range of usual principal value radians )
Range of usual principal value degrees )
arcsine
y
=
arcsin
(
x
)
{\displaystyle y=\arcsin(x)}
x = sin (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
−
π
2
≤
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
≤
90
∘
{\displaystyle -90^{\circ }\leq y\leq 90^{\circ }}
arccosine
y
=
arccos
(
x
)
{\displaystyle y=\arccos(x)}
x = cos (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
0
≤
y
≤
π
{\displaystyle 0\leq y\leq \pi }
0
∘
≤
y
≤
180
∘
{\displaystyle 0^{\circ }\leq y\leq 180^{\circ }}
arctangent
y
=
arctan
(
x
)
{\displaystyle y=\arctan(x)}
x = tan (y )all real numbers
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}
−
90
∘
<
y
<
90
∘
{\displaystyle -90^{\circ }<y<90^{\circ }}
arccotangent
y
=
arccot
(
x
)
{\displaystyle y=\operatorname {arccot}(x)}
x = cot (y )all real numbers
0
<
y
<
π
{\displaystyle 0<y<\pi }
0
∘
<
y
<
180
∘
{\displaystyle 0^{\circ }<y<180^{\circ }}
arcsecant
y
=
arcsec
(
x
)
{\displaystyle y=\operatorname {arcsec}(x)}
x = sec (y )
|
x
|
≥
1
{\displaystyle {\left\vert x\right\vert }\geq 1}
0
≤
y
<
π
2
or
π
2
<
y
≤
π
{\displaystyle 0\leq y<{\frac {\pi }{2}}{\text{ or }}{\frac {\pi }{2}}<y\leq \pi }
0
∘
≤
y
<
90
∘
or
90
∘
<
y
≤
180
∘
{\displaystyle 0^{\circ }\leq y<90^{\circ }{\text{ or }}90^{\circ }<y\leq 180^{\circ }}
arccosecant
y
=
arccsc
(
x
)
{\displaystyle y=\operatorname {arccsc}(x)}
x = csc (y )
|
x
|
≥
1
{\displaystyle {\left\vert x\right\vert }\geq 1}
−
π
2
≤
y
<
0
or
0
<
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y<0{\text{ or }}0<y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
<
0
∘
or
0
∘
<
y
≤
90
∘
{\displaystyle -90^{\circ }\leq y<0^{\circ }{\text{ or }}0^{\circ }<y\leq 90^{\circ }}
Relationships among the inverse trigonometric functions [ sửa ] The usual principal values of the arcsin(x ) (red) and arccos(x ) (blue) functions graphed on the cartesian plane. The usual principal values of the arctan(x ) and arccot(x ) functions graphed on the cartesian plane. Principal values of the arcsec(x ) and arccsc(x ) functions graphed on the cartesian plane. Complementary angles:
arccos
(
x
)
=
π
2
−
arcsin
(
x
)
arccot
(
x
)
=
π
2
−
arctan
(
x
)
arccsc
(
x
)
=
π
2
−
arcsec
(
x
)
{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}
Negative arguments:
arcsin
(
−
x
)
=
−
arcsin
(
x
)
arccos
(
−
x
)
=
π
−
arccos
(
x
)
arctan
(
−
x
)
=
−
arctan
(
x
)
arccot
(
−
x
)
=
π
−
arccot
(
x
)
arcsec
(
−
x
)
=
π
−
arcsec
(
x
)
arccsc
(
−
x
)
=
−
arccsc
(
x
)
{\displaystyle {\begin{aligned}\arcsin(-x)&=-\arcsin(x)\\\arccos(-x)&=\pi -\arccos(x)\\\arctan(-x)&=-\arctan(x)\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot}(x)\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec}(x)\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc}(x)\end{aligned}}}
Reciprocal arguments:
arccos
(
1
x
)
=
arcsec
(
x
)
arcsin
(
1
x
)
=
arccsc
(
x
)
arctan
(
1
x
)
=
π
2
−
arctan
(
x
)
=
arccot
(
x
)
,
if
x
>
0
arctan
(
1
x
)
=
−
π
2
−
arctan
(
x
)
=
arccot
(
x
)
−
π
,
if
x
<
0
arccot
(
1
x
)
=
π
2
−
arccot
(
x
)
=
arctan
(
x
)
,
if
x
>
0
arccot
(
1
x
)
=
3
π
2
−
arccot
(
x
)
=
π
+
arctan
(
x
)
,
if
x
<
0
arcsec
(
1
x
)
=
arccos
(
x
)
arccsc
(
1
x
)
=
arcsin
(
x
)
{\displaystyle {\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}}
Useful identities if one only has a fragment of a sine table:
arccos
(
x
)
=
arcsin
(
1
−
x
2
)
,
if
0
≤
x
≤
1
, from which you get
arccos
(
1
−
x
2
1
+
x
2
)
=
arcsin
(
2
x
1
+
x
2
)
,
if
0
≤
x
≤
1
arcsin
(
1
−
x
2
)
=
π
2
−
sgn
(
x
)
arcsin
(
x
)
arccos
(
x
)
=
1
2
arccos
(
2
x
2
−
1
)
,
if
0
≤
x
≤
1
arcsin
(
x
)
=
1
2
arccos
(
1
−
2
x
2
)
,
if
0
≤
x
≤
1
arcsin
(
x
)
=
arctan
(
x
1
−
x
2
)
arccos
(
x
)
=
arctan
(
1
−
x
2
x
)
arctan
(
x
)
=
arcsin
(
x
1
+
x
2
)
arccot
(
x
)
=
arccos
(
x
1
+
x
2
)
{\displaystyle {\begin{aligned}\arccos(x)&=\arcsin \left({\sqrt {1-x^{2}}}\right)\,,{\text{ if }}0\leq x\leq 1{\text{ , from which you get }}\\\arccos &\left({\frac {1-x^{2}}{1+x^{2}}}\right)=\arcsin \left({\frac {2x}{1+x^{2}}}\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin &\left({\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}-\operatorname {sgn}(x)\arcsin(x)\\\arccos(x)&={\frac {1}{2}}\arccos \left(2x^{2}-1\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin(x)&={\frac {1}{2}}\arccos \left(1-2x^{2}\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin(x)&=\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)\\\arccos(x)&=\arctan \left({\frac {\sqrt {1-x^{2}}}{x}}\right)\\\arctan(x)&=\arcsin \left({\frac {x}{\sqrt {1+x^{2}}}}\right)\\\operatorname {arccot}(x)&=\arccos \left({\frac {x}{\sqrt {1+x^{2}}}}\right)\end{aligned}}}
Whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part if the square was negative real).
A useful form that follows directly from the table above is
arctan
(
x
)
=
arccos
(
1
1
+
x
2
)
,
if
x
≥
0
{\displaystyle \arctan \left(x\right)=\arccos \left({\sqrt {\frac {1}{1+x^{2}}}}\right)\,,{\text{ if }}x\geq 0}
It is obtained by recognizing that
cos
(
arctan
(
x
)
)
=
1
1
+
x
2
=
cos
(
arccos
(
1
1
+
x
2
)
)
{\displaystyle \cos \left(\arctan \left(x\right)\right)={\sqrt {\frac {1}{1+x^{2}}}}=\cos \left(\arccos \left({\sqrt {\frac {1}{1+x^{2}}}}\right)\right)}
From the half-angle formula ,
tan
(
θ
2
)
=
sin
(
θ
)
1
+
cos
(
θ
)
{\displaystyle \tan \left({\tfrac {\theta }{2}}\right)={\tfrac {\sin(\theta )}{1+\cos(\theta )}}}
arcsin
(
x
)
=
2
arctan
(
x
1
+
1
−
x
2
)
arccos
(
x
)
=
2
arctan
(
1
−
x
2
1
+
x
)
,
if
−
1
<
x
≤
1
arctan
(
x
)
=
2
arctan
(
x
1
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ if }}-1<x\leq 1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}}
arctan
(
u
)
±
arctan
(
v
)
=
arctan
(
u
±
v
1
∓
u
v
)
(
mod
π
)
,
u
v
≠
1
.
{\displaystyle \arctan(u)\pm \arctan(v)=\arctan \left({\frac {u\pm v}{1\mp uv}}\right){\pmod {\pi }}\,,\quad uv\neq 1\,.}
This is derived from the tangent addition formula
tan
(
α
±
β
)
=
tan
(
α
)
±
tan
(
β
)
1
∓
tan
(
α
)
tan
(
β
)
,
{\displaystyle \tan(\alpha \pm \beta )={\frac {\tan(\alpha )\pm \tan(\beta )}{1\mp \tan(\alpha )\tan(\beta )}}\,,}
by letting
α
=
arctan
(
u
)
,
β
=
arctan
(
v
)
.
{\displaystyle \alpha =\arctan(u)\,,\quad \beta =\arctan(v)\,.}
[ sửa ] The derivatives for complex values of z are as follows:
d
d
z
arcsin
(
z
)
=
1
1
−
z
2
;
z
≠
−
1
,
+
1
d
d
z
arccos
(
z
)
=
−
1
1
−
z
2
;
z
≠
−
1
,
+
1
d
d
z
arctan
(
z
)
=
1
1
+
z
2
;
z
≠
−
i
,
+
i
d
d
z
arccot
(
z
)
=
−
1
1
+
z
2
;
z
≠
−
i
,
+
i
d
d
z
arcsec
(
z
)
=
1
z
2
1
−
1
z
2
;
z
≠
−
1
,
0
,
+
1
d
d
z
arccsc
(
z
)
=
−
1
z
2
1
−
1
z
2
;
z
≠
−
1
,
0
,
+
1
{\displaystyle {\begin{aligned}{\frac {d}{dz}}\arcsin(z)&{}={\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {d}{dz}}\arccos(z)&{}=-{\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {d}{dz}}\arctan(z)&{}={\frac {1}{1+z^{2}}}\;;&z&{}\neq -i,+i\\{\frac {d}{dz}}\operatorname {arccot}(z)&{}=-{\frac {1}{1+z^{2}}}\;;&z&{}\neq -i,+i\\{\frac {d}{dz}}\operatorname {arcsec}(z)&{}={\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\\{\frac {d}{dz}}\operatorname {arccsc}(z)&{}=-{\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\end{aligned}}}
Only for real values of x :
d
d
x
arcsec
(
x
)
=
1
|
x
|
x
2
−
1
;
|
x
|
>
1
d
d
x
arccsc
(
x
)
=
−
1
|
x
|
x
2
−
1
;
|
x
|
>
1
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arcsec}(x)&{}={\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\\{\frac {d}{dx}}\operatorname {arccsc}(x)&{}=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\end{aligned}}}
For a sample derivation: if
θ
=
arcsin
(
x
)
{\displaystyle \theta =\arcsin(x)}
d
arcsin
(
x
)
d
x
=
d
θ
d
sin
(
θ
)
=
d
θ
cos
(
θ
)
d
θ
=
1
cos
(
θ
)
=
1
1
−
sin
2
(
θ
)
=
1
1
−
x
2
{\displaystyle {\frac {d\arcsin(x)}{dx}}={\frac {d\theta }{d\sin(\theta )}}={\frac {d\theta }{\cos(\theta )\,d\theta }}={\frac {1}{\cos(\theta )}}={\frac {1}{\sqrt {1-\sin ^{2}(\theta )}}}={\frac {1}{\sqrt {1-x^{2}}}}}
Expression as definite integrals [ sửa ] Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
arctan
(
x
)
=
∫
0
x
1
z
2
+
1
d
z
,
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
arcsec
(
x
)
=
∫
1
x
1
z
z
2
−
1
d
z
=
π
+
∫
−
x
−
1
1
z
z
2
−
1
d
z
,
x
≥
1
arccsc
(
x
)
=
∫
x
∞
1
z
z
2
−
1
d
z
=
∫
−
∞
−
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\int _{-\infty }^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\end{aligned}}}
When x equals 1, the integrals with limited domains are improper integrals , but still well-defined.
Similar to the sine and cosine functions, the inverse trigonometric functions can also be calculated using power series , as follows. For arcsine, the series can be derived by expanding its derivative,
1
1
−
z
2
{\textstyle {\tfrac {1}{\sqrt {1-z^{2}}}}}
binomial series , and integrating term by term (using the integral definition as above). The series for arctangent can similarly be derived by expanding its derivative
1
1
+
z
2
{\textstyle {\frac {1}{1+z^{2}}}}
geometric series , and applying the integral definition above (see Leibniz series ).
arcsin
(
z
)
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}
arctan
(
z
)
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq i,-i}
Series for the other inverse trigonometric functions can be given in terms of these according to the relationships given above. For example,
arccos
(
x
)
=
π
/
2
−
arcsin
(
x
)
{\displaystyle \arccos(x)=\pi /2-\arcsin(x)}
arccsc
(
x
)
=
arcsin
(
1
/
x
)
{\displaystyle \operatorname {arccsc}(x)=\arcsin(1/x)}
2
(
arcsin
(
x
2
)
)
2
=
∑
n
=
1
∞
x
2
n
n
2
(
2
n
n
)
.
{\displaystyle 2\left(\arcsin \left({\frac {x}{2}}\right)\right)^{2}=\sum _{n=1}^{\infty }{\frac {x^{2n}}{n^{2}{\binom {2n}{n}}}}.}
Leonhard Euler found a series for the arctangent that converges more quickly than its Taylor series :
arctan
(
z
)
=
z
1
+
z
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
z
2
(
2
k
+
1
)
(
1
+
z
2
)
.
{\displaystyle \arctan(z)={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}
(The term in the sum for n = 0 is the empty product , so is 1.)
Alternatively, this can be expressed as
arctan
(
z
)
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
z
2
n
+
1
(
1
+
z
2
)
n
+
1
.
{\displaystyle \arctan(z)=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}
Another series for the arctangent function is given by
arctan
(
z
)
=
i
∑
n
=
1
∞
1
2
n
−
1
(
1
(
1
+
2
i
/
z
)
2
n
−
1
−
1
(
1
−
2
i
/
z
)
2
n
−
1
)
,
{\displaystyle \arctan(z)=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{(1+2i/z)^{2n-1}}}-{\frac {1}{(1-2i/z)^{2n-1}}}\right),}
where
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
imaginary unit .
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Indefinite integrals of inverse trigonometric functions [ sửa ] For real and complex values of z :
∫
arcsin
(
z
)
d
z
=
z
arcsin
(
z
)
+
1
−
z
2
+
C
∫
arccos
(
z
)
d
z
=
z
arccos
(
z
)
−
1
−
z
2
+
C
∫
arctan
(
z
)
d
z
=
z
arctan
(
z
)
−
1
2
ln
(
1
+
z
2
)
+
C
∫
arccot
(
z
)
d
z
=
z
arccot
(
z
)
+
1
2
ln
(
1
+
z
2
)
+
C
∫
arcsec
(
z
)
d
z
=
z
arcsec
(
z
)
−
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
∫
arccsc
(
z
)
d
z
=
z
arccsc
(
z
)
+
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}
For real x ≥ 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
For all real x not between -1 and 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\end{aligned}}}
The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions :
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
arcosh
(
|
x
|
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
arcosh
(
|
x
|
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {arcosh} (|x|)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {arcosh} (|x|)+C\\\end{aligned}}}
The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.
All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.
Using
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,dv=uv-\int v\,du}
integration by parts ), set
u
=
arcsin
(
x
)
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}}
Then
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
−
∫
x
1
−
x
2
d
x
,
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,dx,}
which by the simple substitution
w
=
1
−
x
2
,
d
w
=
−
2
x
d
x
{\displaystyle w=1-x^{2},\ dw=-2x\,dx}
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
These functions may also be expressed using complex logarithms . This extends their domains to the complex plane in a natural fashion. The following identities for principal values of the functions hold everywhere that they are defined, even on their branch cuts.
arcsin
(
z
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
=
i
ln
(
1
−
z
2
−
i
z
)
=
arccsc
(
1
z
)
arccos
(
z
)
=
−
i
ln
(
i
1
−
z
2
+
z
)
=
π
2
−
arcsin
(
z
)
=
arcsec
(
1
z
)
arctan
(
z
)
=
−
i
2
ln
(
i
−
z
i
+
z
)
=
−
i
2
ln
(
1
+
i
z
1
−
i
z
)
=
arccot
(
1
z
)
arccot
(
z
)
=
−
i
2
ln
(
z
+
i
z
−
i
)
=
−
i
2
ln
(
i
z
−
1
i
z
+
1
)
=
arctan
(
1
z
)
arcsec
(
z
)
=
−
i
ln
(
i
1
−
1
z
2
+
1
z
)
=
π
2
−
arccsc
(
z
)
=
arccos
(
1
z
)
arccsc
(
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
=
i
ln
(
1
−
1
z
2
−
i
z
)
=
arcsin
(
1
z
)
{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}
Because all of the inverse trigonometric functions output an angle of a right triangle, they can be generalized by using Euler's formula to form a right triangle in the complex plane. Algebraically, this gives us:
c
e
i
θ
=
c
cos
(
θ
)
+
i
c
sin
(
θ
)
{\displaystyle ce^{i\theta }=c\cos(\theta )+ic\sin(\theta )}
or
c
e
i
θ
=
a
+
i
b
{\displaystyle ce^{i\theta }=a+ib}
where
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
θ
{\displaystyle \theta }
e
ln
(
c
)
+
i
θ
=
a
+
i
b
ln
c
+
i
θ
=
ln
(
a
+
i
b
)
θ
=
Im
(
ln
(
a
+
i
b
)
)
{\displaystyle {\begin{aligned}e^{\ln(c)+i\theta }&=a+ib\\\ln c+i\theta &=\ln(a+ib)\\\theta &=\operatorname {Im} \left(\ln(a+ib)\right)\end{aligned}}}
or
θ
=
−
i
ln
(
a
+
i
b
c
)
{\displaystyle \theta =-i\ln \left({\frac {a+ib}{c}}\right)}
Simply taking the imaginary part works for any real-valued
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
ln
(
a
+
b
i
)
{\displaystyle \ln(a+bi)}
c
{\displaystyle c}
z
{\displaystyle z}
Pythagorean Theorem relation
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
The table below shows the values of a, b, and c for each of the inverse trig functions and the equivalent expressions for
θ
{\displaystyle \theta }
a
b
c
−
i
ln
(
a
+
i
b
c
)
θ
θ
a
,
b
∈
R
arcsin
(
z
)
1
−
z
2
z
1
−
i
ln
(
1
−
z
2
+
i
z
1
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
Im
(
ln
(
1
−
z
2
+
i
z
)
)
arccos
(
z
)
z
1
−
z
2
1
−
i
ln
(
z
+
i
1
−
z
2
1
)
=
−
i
ln
(
z
+
z
2
−
1
)
Im
(
ln
(
z
+
z
2
−
1
)
)
arctan
(
z
)
1
z
1
+
z
2
−
i
ln
(
1
+
i
z
1
+
z
2
)
=
−
i
ln
(
1
+
i
z
1
+
z
2
)
Im
(
ln
(
1
+
i
z
)
)
arccot
(
z
)
z
1
z
2
+
1
−
i
ln
(
z
+
i
z
2
+
1
)
=
−
i
ln
(
z
+
i
z
2
+
1
)
Im
(
ln
(
z
+
i
)
)
arcsec
(
z
)
1
z
2
−
1
z
−
i
ln
(
1
+
i
z
2
−
1
z
)
=
−
i
ln
(
1
z
+
1
z
2
−
1
)
Im
(
ln
(
1
z
+
1
z
2
−
1
)
)
arccsc
(
z
)
z
2
−
1
1
z
−
i
ln
(
z
2
−
1
+
i
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
Im
(
ln
(
1
−
1
z
2
+
i
z
)
)
{\displaystyle {\begin{aligned}&a&&b&&c&&-i\ln \left({\frac {a+ib}{c}}\right)&&\theta &&\theta _{a,b\in \mathbb {R} }\\\arcsin(z)\ \ &{\sqrt {1-z^{2}}}&&z&&1&&-i\ln \left({\frac {{\sqrt {1-z^{2}}}+iz}{1}}\right)&&=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-z^{2}}}+iz\right)\right)\\\arccos(z)\ \ &z&&{\sqrt {1-z^{2}}}&&1&&-i\ln \left({\frac {z+i{\sqrt {1-z^{2}}}}{1}}\right)&&=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)&&\operatorname {Im} \left(\ln \left(z+{\sqrt {z^{2}-1}}\right)\right)\\\arctan(z)\ \ &1&&z&&{\sqrt {1+z^{2}}}&&-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&=-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&\operatorname {Im} \left(\ln \left(1+iz\right)\right)\\\operatorname {arccot}(z)\ \ &z&&1&&{\sqrt {z^{2}+1}}&&-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&=-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&\operatorname {Im} \left(\ln \left(z+i\right)\right)\\\operatorname {arcsec}(z)\ \ &1&&{\sqrt {z^{2}-1}}&&z&&-i\ln \left({\frac {1+i{\sqrt {z^{2}-1}}}{z}}\right)&&=-i\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)&&\operatorname {Im} \left(\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)\right)\\\operatorname {arccsc}(z)\ \ &{\sqrt {z^{2}-1}}&&1&&z&&-i\ln \left({\frac {{\sqrt {z^{2}-1}}+i}{z}}\right)&&=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)\right)\\\end{aligned}}}
In order to match the principal branch of the natural log and square root functions to the usual principal branch of the inverse trig functions, the particular form of the simplified formulation matters. The formulations given in the two rightmost columns assume
Im
(
ln
z
)
∈
(
−
π
,
π
]
{\displaystyle \operatorname {Im} \left(\ln z\right)\in (-\pi ,\pi ]}
Re
(
z
)
≥
0
{\displaystyle \operatorname {Re} \left({\sqrt {z}}\right)\geq 0}
Im
(
ln
z
)
∈
[
0
,
2
π
)
{\displaystyle \operatorname {Im} \left(\ln z\right)\in [0,2\pi )}
Im
(
z
)
≥
0
{\displaystyle \operatorname {Im} \left({\sqrt {z}}\right)\geq 0}
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
Re
(
θ
)
>
π
{\displaystyle \operatorname {Re} (\theta )>\pi }
In this sense, all of the inverse trig functions can be thought of as specific cases of the complex-valued log function. Since these definition work for any complex-valued
z
{\displaystyle z}
hyperbolic angles as outputs and can be used to further define the inverse hyperbolic functions . Elementary proofs of the relations may also proceed via expansion to exponential forms of the trigonometric functions.
sin
(
ϕ
)
=
z
ϕ
=
arcsin
(
z
)
{\displaystyle {\begin{aligned}\sin(\phi )&=z\\\phi &=\arcsin(z)\end{aligned}}}
Using the exponential definition of sine , and letting
ξ
=
e
i
ϕ
,
{\displaystyle \xi =e^{i\phi },}
z
=
e
i
ϕ
−
e
−
i
ϕ
2
i
2
i
z
=
ξ
−
1
ξ
0
=
ξ
2
−
2
i
z
ξ
−
1
ξ
=
i
z
±
1
−
z
2
ϕ
=
−
i
ln
(
i
z
±
1
−
z
2
)
{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}
(the positive branch is chosen)
ϕ
=
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
{\displaystyle \phi =\arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)}
Color wheel graphs of inverse trigonometric functions in the complex plane
arcsin
(
z
)
{\displaystyle \arcsin(z)}
arccos
(
z
)
{\displaystyle \arccos(z)}
arctan
(
z
)
{\displaystyle \arctan(z)}
arccsc
(
z
)
{\displaystyle \operatorname {arccsc}(z)}
arcsec
(
z
)
{\displaystyle \operatorname {arcsec}(z)}
arccot
(
z
)
{\displaystyle \operatorname {arccot}(z)}
Expression as definite integrals [ sửa ] Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
arctan
(
x
)
=
∫
0
x
1
z
2
+
1
d
z
,
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
arcsec
(
x
)
=
∫
1
x
1
z
z
2
−
1
d
z
=
π
+
∫
−
x
−
1
1
z
z
2
−
1
d
z
,
x
≥
1
arccsc
(
x
)
=
∫
x
∞
1
z
z
2
−
1
d
z
=
∫
−
∞
−
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\int _{-\infty }^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\end{aligned}}}
When x equals 1, the integrals with limited domains are improper integrals , but still well-defined.
Similar to the sine and cosine functions, the inverse trigonometric functions can also be calculated using power series , as follows. For arcsine, the series can be derived by expanding its derivative,
1
1
−
z
2
{\textstyle {\tfrac {1}{\sqrt {1-z^{2}}}}}
binomial series , and integrating term by term (using the integral definition as above). The series for arctangent can similarly be derived by expanding its derivative
1
1
+
z
2
{\textstyle {\frac {1}{1+z^{2}}}}
geometric series , and applying the integral definition above (see Leibniz series ).
arcsin
(
z
)
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}
arctan
(
z
)
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq i,-i}
Series for the other inverse trigonometric functions can be given in terms of these according to the relationships given above. For example,
arccos
(
x
)
=
π
/
2
−
arcsin
(
x
)
{\displaystyle \arccos(x)=\pi /2-\arcsin(x)}
arccsc
(
x
)
=
arcsin
(
1
/
x
)
{\displaystyle \operatorname {arccsc}(x)=\arcsin(1/x)}
2
(
arcsin
(
x
2
)
)
2
=
∑
n
=
1
∞
x
2
n
n
2
(
2
n
n
)
.
{\displaystyle 2\left(\arcsin \left({\frac {x}{2}}\right)\right)^{2}=\sum _{n=1}^{\infty }{\frac {x^{2n}}{n^{2}{\binom {2n}{n}}}}.}
Leonhard Euler found a series for the arctangent that converges more quickly than its Taylor series :
arctan
(
z
)
=
z
1
+
z
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
z
2
(
2
k
+
1
)
(
1
+
z
2
)
.
{\displaystyle \arctan(z)={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}
(The term in the sum for n = 0 is the empty product , so is 1.)
Alternatively, this can be expressed as
arctan
(
z
)
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
z
2
n
+
1
(
1
+
z
2
)
n
+
1
.
{\displaystyle \arctan(z)=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}
Another series for the arctangent function is given by
arctan
(
z
)
=
i
∑
n
=
1
∞
1
2
n
−
1
(
1
(
1
+
2
i
/
z
)
2
n
−
1
−
1
(
1
−
2
i
/
z
)
2
n
−
1
)
,
{\displaystyle \arctan(z)=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{(1+2i/z)^{2n-1}}}-{\frac {1}{(1-2i/z)^{2n-1}}}\right),}
where
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
imaginary unit .
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Indefinite integrals of inverse trigonometric functions [ sửa ] For real and complex values of z :
∫
arcsin
(
z
)
d
z
=
z
arcsin
(
z
)
+
1
−
z
2
+
C
∫
arccos
(
z
)
d
z
=
z
arccos
(
z
)
−
1
−
z
2
+
C
∫
arctan
(
z
)
d
z
=
z
arctan
(
z
)
−
1
2
ln
(
1
+
z
2
)
+
C
∫
arccot
(
z
)
d
z
=
z
arccot
(
z
)
+
1
2
ln
(
1
+
z
2
)
+
C
∫
arcsec
(
z
)
d
z
=
z
arcsec
(
z
)
−
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
∫
arccsc
(
z
)
d
z
=
z
arccsc
(
z
)
+
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}
For real x ≥ 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
For all real x not between -1 and 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\end{aligned}}}
The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions :
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
arcosh
(
|
x
|
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
arcosh
(
|
x
|
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {arcosh} (|x|)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {arcosh} (|x|)+C\\\end{aligned}}}
The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.
All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.
Using
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,dv=uv-\int v\,du}
integration by parts ), set
u
=
arcsin
(
x
)
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}}
Then
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
−
∫
x
1
−
x
2
d
x
,
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,dx,}
which by the simple substitution
w
=
1
−
x
2
,
d
w
=
−
2
x
d
x
{\displaystyle w=1-x^{2},\ dw=-2x\,dx}
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
These functions may also be expressed using complex logarithms . This extends their domains to the complex plane in a natural fashion. The following identities for principal values of the functions hold everywhere that they are defined, even on their branch cuts.
arcsin
(
z
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
=
i
ln
(
1
−
z
2
−
i
z
)
=
arccsc
(
1
z
)
arccos
(
z
)
=
−
i
ln
(
i
1
−
z
2
+
z
)
=
π
2
−
arcsin
(
z
)
=
arcsec
(
1
z
)
arctan
(
z
)
=
−
i
2
ln
(
i
−
z
i
+
z
)
=
−
i
2
ln
(
1
+
i
z
1
−
i
z
)
=
arccot
(
1
z
)
arccot
(
z
)
=
−
i
2
ln
(
z
+
i
z
−
i
)
=
−
i
2
ln
(
i
z
−
1
i
z
+
1
)
=
arctan
(
1
z
)
arcsec
(
z
)
=
−
i
ln
(
i
1
−
1
z
2
+
1
z
)
=
π
2
−
arccsc
(
z
)
=
arccos
(
1
z
)
arccsc
(
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
=
i
ln
(
1
−
1
z
2
−
i
z
)
=
arcsin
(
1
z
)
{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}
Because all of the inverse trigonometric functions output an angle of a right triangle, they can be generalized by using Euler's formula to form a right triangle in the complex plane. Algebraically, this gives us:
c
e
i
θ
=
c
cos
(
θ
)
+
i
c
sin
(
θ
)
{\displaystyle ce^{i\theta }=c\cos(\theta )+ic\sin(\theta )}
or
c
e
i
θ
=
a
+
i
b
{\displaystyle ce^{i\theta }=a+ib}
where
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
θ
{\displaystyle \theta }
e
ln
(
c
)
+
i
θ
=
a
+
i
b
ln
c
+
i
θ
=
ln
(
a
+
i
b
)
θ
=
Im
(
ln
(
a
+
i
b
)
)
{\displaystyle {\begin{aligned}e^{\ln(c)+i\theta }&=a+ib\\\ln c+i\theta &=\ln(a+ib)\\\theta &=\operatorname {Im} \left(\ln(a+ib)\right)\end{aligned}}}
or
θ
=
−
i
ln
(
a
+
i
b
c
)
{\displaystyle \theta =-i\ln \left({\frac {a+ib}{c}}\right)}
Simply taking the imaginary part works for any real-valued
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
ln
(
a
+
b
i
)
{\displaystyle \ln(a+bi)}
c
{\displaystyle c}
z
{\displaystyle z}
Pythagorean Theorem relation
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
The table below shows the values of a, b, and c for each of the inverse trig functions and the equivalent expressions for
θ
{\displaystyle \theta }
a
b
c
−
i
ln
(
a
+
i
b
c
)
θ
θ
a
,
b
∈
R
arcsin
(
z
)
1
−
z
2
z
1
−
i
ln
(
1
−
z
2
+
i
z
1
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
Im
(
ln
(
1
−
z
2
+
i
z
)
)
arccos
(
z
)
z
1
−
z
2
1
−
i
ln
(
z
+
i
1
−
z
2
1
)
=
−
i
ln
(
z
+
z
2
−
1
)
Im
(
ln
(
z
+
z
2
−
1
)
)
arctan
(
z
)
1
z
1
+
z
2
−
i
ln
(
1
+
i
z
1
+
z
2
)
=
−
i
ln
(
1
+
i
z
1
+
z
2
)
Im
(
ln
(
1
+
i
z
)
)
arccot
(
z
)
z
1
z
2
+
1
−
i
ln
(
z
+
i
z
2
+
1
)
=
−
i
ln
(
z
+
i
z
2
+
1
)
Im
(
ln
(
z
+
i
)
)
arcsec
(
z
)
1
z
2
−
1
z
−
i
ln
(
1
+
i
z
2
−
1
z
)
=
−
i
ln
(
1
z
+
1
z
2
−
1
)
Im
(
ln
(
1
z
+
1
z
2
−
1
)
)
arccsc
(
z
)
z
2
−
1
1
z
−
i
ln
(
z
2
−
1
+
i
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
Im
(
ln
(
1
−
1
z
2
+
i
z
)
)
{\displaystyle {\begin{aligned}&a&&b&&c&&-i\ln \left({\frac {a+ib}{c}}\right)&&\theta &&\theta _{a,b\in \mathbb {R} }\\\arcsin(z)\ \ &{\sqrt {1-z^{2}}}&&z&&1&&-i\ln \left({\frac {{\sqrt {1-z^{2}}}+iz}{1}}\right)&&=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-z^{2}}}+iz\right)\right)\\\arccos(z)\ \ &z&&{\sqrt {1-z^{2}}}&&1&&-i\ln \left({\frac {z+i{\sqrt {1-z^{2}}}}{1}}\right)&&=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)&&\operatorname {Im} \left(\ln \left(z+{\sqrt {z^{2}-1}}\right)\right)\\\arctan(z)\ \ &1&&z&&{\sqrt {1+z^{2}}}&&-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&=-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&\operatorname {Im} \left(\ln \left(1+iz\right)\right)\\\operatorname {arccot}(z)\ \ &z&&1&&{\sqrt {z^{2}+1}}&&-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&=-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&\operatorname {Im} \left(\ln \left(z+i\right)\right)\\\operatorname {arcsec}(z)\ \ &1&&{\sqrt {z^{2}-1}}&&z&&-i\ln \left({\frac {1+i{\sqrt {z^{2}-1}}}{z}}\right)&&=-i\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)&&\operatorname {Im} \left(\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)\right)\\\operatorname {arccsc}(z)\ \ &{\sqrt {z^{2}-1}}&&1&&z&&-i\ln \left({\frac {{\sqrt {z^{2}-1}}+i}{z}}\right)&&=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)\right)\\\end{aligned}}}
In order to match the principal branch of the natural log and square root functions to the usual principal branch of the inverse trig functions, the particular form of the simplified formulation matters. The formulations given in the two rightmost columns assume
Im
(
ln
z
)
∈
(
−
π
,
π
]
{\displaystyle \operatorname {Im} \left(\ln z\right)\in (-\pi ,\pi ]}
Re
(
z
)
≥
0
{\displaystyle \operatorname {Re} \left({\sqrt {z}}\right)\geq 0}
Im
(
ln
z
)
∈
[
0
,
2
π
)
{\displaystyle \operatorname {Im} \left(\ln z\right)\in [0,2\pi )}
Im
(
z
)
≥
0
{\displaystyle \operatorname {Im} \left({\sqrt {z}}\right)\geq 0}
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
Re
(
θ
)
>
π
{\displaystyle \operatorname {Re} (\theta )>\pi }
In this sense, all of the inverse trig functions can be thought of as specific cases of the complex-valued log function. Since these definition work for any complex-valued
z
{\displaystyle z}
hyperbolic angles as outputs and can be used to further define the inverse hyperbolic functions . Elementary proofs of the relations may also proceed via expansion to exponential forms of the trigonometric functions.
sin
(
ϕ
)
=
z
ϕ
=
arcsin
(
z
)
{\displaystyle {\begin{aligned}\sin(\phi )&=z\\\phi &=\arcsin(z)\end{aligned}}}
Using the exponential definition of sine , and letting
ξ
=
e
i
ϕ
,
{\displaystyle \xi =e^{i\phi },}
z
=
e
i
ϕ
−
e
−
i
ϕ
2
i
2
i
z
=
ξ
−
1
ξ
0
=
ξ
2
−
2
i
z
ξ
−
1
ξ
=
i
z
±
1
−
z
2
ϕ
=
−
i
ln
(
i
z
±
1
−
z
2
)
{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}
(the positive branch is chosen)
ϕ
=
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
{\displaystyle \phi =\arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)}
Color wheel graphs of inverse trigonometric functions in the complex plane
arcsin
(
z
)
{\displaystyle \arcsin(z)}
arccos
(
z
)
{\displaystyle \arccos(z)}
arctan
(
z
)
{\displaystyle \arctan(z)}
arccsc
(
z
)
{\displaystyle \operatorname {arccsc}(z)}
arcsec
(
z
)
{\displaystyle \operatorname {arcsec}(z)}
arccot
(
z
)
{\displaystyle \operatorname {arccot}(z)}
Expression as definite integrals [ sửa ] Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
arctan
(
x
)
=
∫
0
x
1
z
2
+
1
d
z
,
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
arcsec
(
x
)
=
∫
1
x
1
z
z
2
−
1
d
z
=
π
+
∫
−
x
−
1
1
z
z
2
−
1
d
z
,
x
≥
1
arccsc
(
x
)
=
∫
x
∞
1
z
z
2
−
1
d
z
=
∫
−
∞
−
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\int _{-\infty }^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\end{aligned}}}
When x equals 1, the integrals with limited domains are improper integrals , but still well-defined.
Similar to the sine and cosine functions, the inverse trigonometric functions can also be calculated using power series , as follows. For arcsine, the series can be derived by expanding its derivative,
1
1
−
z
2
{\textstyle {\tfrac {1}{\sqrt {1-z^{2}}}}}
binomial series , and integrating term by term (using the integral definition as above). The series for arctangent can similarly be derived by expanding its derivative
1
1
+
z
2
{\textstyle {\frac {1}{1+z^{2}}}}
geometric series , and applying the integral definition above (see Leibniz series ).
arcsin
(
z
)
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}
arctan
(
z
)
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq i,-i}
Series for the other inverse trigonometric functions can be given in terms of these according to the relationships given above. For example,
arccos
(
x
)
=
π
/
2
−
arcsin
(
x
)
{\displaystyle \arccos(x)=\pi /2-\arcsin(x)}
arccsc
(
x
)
=
arcsin
(
1
/
x
)
{\displaystyle \operatorname {arccsc}(x)=\arcsin(1/x)}
2
(
arcsin
(
x
2
)
)
2
=
∑
n
=
1
∞
x
2
n
n
2
(
2
n
n
)
.
{\displaystyle 2\left(\arcsin \left({\frac {x}{2}}\right)\right)^{2}=\sum _{n=1}^{\infty }{\frac {x^{2n}}{n^{2}{\binom {2n}{n}}}}.}
Leonhard Euler found a series for the arctangent that converges more quickly than its Taylor series :
arctan
(
z
)
=
z
1
+
z
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
z
2
(
2
k
+
1
)
(
1
+
z
2
)
.
{\displaystyle \arctan(z)={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}
(The term in the sum for n = 0 is the empty product , so is 1.)
Alternatively, this can be expressed as
arctan
(
z
)
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
z
2
n
+
1
(
1
+
z
2
)
n
+
1
.
{\displaystyle \arctan(z)=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}
Another series for the arctangent function is given by
arctan
(
z
)
=
i
∑
n
=
1
∞
1
2
n
−
1
(
1
(
1
+
2
i
/
z
)
2
n
−
1
−
1
(
1
−
2
i
/
z
)
2
n
−
1
)
,
{\displaystyle \arctan(z)=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{(1+2i/z)^{2n-1}}}-{\frac {1}{(1-2i/z)^{2n-1}}}\right),}
where
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
imaginary unit .
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Indefinite integrals of inverse trigonometric functions [ sửa ] For real and complex values of z :
∫
arcsin
(
z
)
d
z
=
z
arcsin
(
z
)
+
1
−
z
2
+
C
∫
arccos
(
z
)
d
z
=
z
arccos
(
z
)
−
1
−
z
2
+
C
∫
arctan
(
z
)
d
z
=
z
arctan
(
z
)
−
1
2
ln
(
1
+
z
2
)
+
C
∫
arccot
(
z
)
d
z
=
z
arccot
(
z
)
+
1
2
ln
(
1
+
z
2
)
+
C
∫
arcsec
(
z
)
d
z
=
z
arcsec
(
z
)
−
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
∫
arccsc
(
z
)
d
z
=
z
arccsc
(
z
)
+
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}
For real x ≥ 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
For all real x not between -1 and 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\end{aligned}}}
The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions :
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
arcosh
(
|
x
|
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
arcosh
(
|
x
|
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {arcosh} (|x|)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {arcosh} (|x|)+C\\\end{aligned}}}
The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.
All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.
Using
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,dv=uv-\int v\,du}
integration by parts ), set
u
=
arcsin
(
x
)
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}}
Then
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
−
∫
x
1
−
x
2
d
x
,
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,dx,}
which by the simple substitution
w
=
1
−
x
2
,
d
w
=
−
2
x
d
x
{\displaystyle w=1-x^{2},\ dw=-2x\,dx}
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
These functions may also be expressed using complex logarithms . This extends their domains to the complex plane in a natural fashion. The following identities for principal values of the functions hold everywhere that they are defined, even on their branch cuts.
arcsin
(
z
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
=
i
ln
(
1
−
z
2
−
i
z
)
=
arccsc
(
1
z
)
arccos
(
z
)
=
−
i
ln
(
i
1
−
z
2
+
z
)
=
π
2
−
arcsin
(
z
)
=
arcsec
(
1
z
)
arctan
(
z
)
=
−
i
2
ln
(
i
−
z
i
+
z
)
=
−
i
2
ln
(
1
+
i
z
1
−
i
z
)
=
arccot
(
1
z
)
arccot
(
z
)
=
−
i
2
ln
(
z
+
i
z
−
i
)
=
−
i
2
ln
(
i
z
−
1
i
z
+
1
)
=
arctan
(
1
z
)
arcsec
(
z
)
=
−
i
ln
(
i
1
−
1
z
2
+
1
z
)
=
π
2
−
arccsc
(
z
)
=
arccos
(
1
z
)
arccsc
(
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
=
i
ln
(
1
−
1
z
2
−
i
z
)
=
arcsin
(
1
z
)
{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}
Because all of the inverse trigonometric functions output an angle of a right triangle, they can be generalized by using Euler's formula to form a right triangle in the complex plane. Algebraically, this gives us:
c
e
i
θ
=
c
cos
(
θ
)
+
i
c
sin
(
θ
)
{\displaystyle ce^{i\theta }=c\cos(\theta )+ic\sin(\theta )}
or
c
e
i
θ
=
a
+
i
b
{\displaystyle ce^{i\theta }=a+ib}
where
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
θ
{\displaystyle \theta }
e
ln
(
c
)
+
i
θ
=
a
+
i
b
ln
c
+
i
θ
=
ln
(
a
+
i
b
)
θ
=
Im
(
ln
(
a
+
i
b
)
)
{\displaystyle {\begin{aligned}e^{\ln(c)+i\theta }&=a+ib\\\ln c+i\theta &=\ln(a+ib)\\\theta &=\operatorname {Im} \left(\ln(a+ib)\right)\end{aligned}}}
or
θ
=
−
i
ln
(
a
+
i
b
c
)
{\displaystyle \theta =-i\ln \left({\frac {a+ib}{c}}\right)}
Simply taking the imaginary part works for any real-valued
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
ln
(
a
+
b
i
)
{\displaystyle \ln(a+bi)}
c
{\displaystyle c}
z
{\displaystyle z}
Pythagorean Theorem relation
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
The table below shows the values of a, b, and c for each of the inverse trig functions and the equivalent expressions for
θ
{\displaystyle \theta }
a
b
c
−
i
ln
(
a
+
i
b
c
)
θ
θ
a
,
b
∈
R
arcsin
(
z
)
1
−
z
2
z
1
−
i
ln
(
1
−
z
2
+
i
z
1
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
Im
(
ln
(
1
−
z
2
+
i
z
)
)
arccos
(
z
)
z
1
−
z
2
1
−
i
ln
(
z
+
i
1
−
z
2
1
)
=
−
i
ln
(
z
+
z
2
−
1
)
Im
(
ln
(
z
+
z
2
−
1
)
)
arctan
(
z
)
1
z
1
+
z
2
−
i
ln
(
1
+
i
z
1
+
z
2
)
=
−
i
ln
(
1
+
i
z
1
+
z
2
)
Im
(
ln
(
1
+
i
z
)
)
arccot
(
z
)
z
1
z
2
+
1
−
i
ln
(
z
+
i
z
2
+
1
)
=
−
i
ln
(
z
+
i
z
2
+
1
)
Im
(
ln
(
z
+
i
)
)
arcsec
(
z
)
1
z
2
−
1
z
−
i
ln
(
1
+
i
z
2
−
1
z
)
=
−
i
ln
(
1
z
+
1
z
2
−
1
)
Im
(
ln
(
1
z
+
1
z
2
−
1
)
)
arccsc
(
z
)
z
2
−
1
1
z
−
i
ln
(
z
2
−
1
+
i
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
Im
(
ln
(
1
−
1
z
2
+
i
z
)
)
{\displaystyle {\begin{aligned}&a&&b&&c&&-i\ln \left({\frac {a+ib}{c}}\right)&&\theta &&\theta _{a,b\in \mathbb {R} }\\\arcsin(z)\ \ &{\sqrt {1-z^{2}}}&&z&&1&&-i\ln \left({\frac {{\sqrt {1-z^{2}}}+iz}{1}}\right)&&=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-z^{2}}}+iz\right)\right)\\\arccos(z)\ \ &z&&{\sqrt {1-z^{2}}}&&1&&-i\ln \left({\frac {z+i{\sqrt {1-z^{2}}}}{1}}\right)&&=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)&&\operatorname {Im} \left(\ln \left(z+{\sqrt {z^{2}-1}}\right)\right)\\\arctan(z)\ \ &1&&z&&{\sqrt {1+z^{2}}}&&-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&=-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&\operatorname {Im} \left(\ln \left(1+iz\right)\right)\\\operatorname {arccot}(z)\ \ &z&&1&&{\sqrt {z^{2}+1}}&&-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&=-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&\operatorname {Im} \left(\ln \left(z+i\right)\right)\\\operatorname {arcsec}(z)\ \ &1&&{\sqrt {z^{2}-1}}&&z&&-i\ln \left({\frac {1+i{\sqrt {z^{2}-1}}}{z}}\right)&&=-i\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)&&\operatorname {Im} \left(\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)\right)\\\operatorname {arccsc}(z)\ \ &{\sqrt {z^{2}-1}}&&1&&z&&-i\ln \left({\frac {{\sqrt {z^{2}-1}}+i}{z}}\right)&&=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)\right)\\\end{aligned}}}
In order to match the principal branch of the natural log and square root functions to the usual principal branch of the inverse trig functions, the particular form of the simplified formulation matters. The formulations given in the two rightmost columns assume
Im
(
ln
z
)
∈
(
−
π
,
π
]
{\displaystyle \operatorname {Im} \left(\ln z\right)\in (-\pi ,\pi ]}
Re
(
z
)
≥
0
{\displaystyle \operatorname {Re} \left({\sqrt {z}}\right)\geq 0}
Im
(
ln
z
)
∈
[
0
,
2
π
)
{\displaystyle \operatorname {Im} \left(\ln z\right)\in [0,2\pi )}
Im
(
z
)
≥
0
{\displaystyle \operatorname {Im} \left({\sqrt {z}}\right)\geq 0}
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
Re
(
θ
)
>
π
{\displaystyle \operatorname {Re} (\theta )>\pi }
In this sense, all of the inverse trig functions can be thought of as specific cases of the complex-valued log function. Since these definition work for any complex-valued
z
{\displaystyle z}
hyperbolic angles as outputs and can be used to further define the inverse hyperbolic functions . Elementary proofs of the relations may also proceed via expansion to exponential forms of the trigonometric functions.
sin
(
ϕ
)
=
z
ϕ
=
arcsin
(
z
)
{\displaystyle {\begin{aligned}\sin(\phi )&=z\\\phi &=\arcsin(z)\end{aligned}}}
Using the exponential definition of sine , and letting
ξ
=
e
i
ϕ
,
{\displaystyle \xi =e^{i\phi },}
z
=
e
i
ϕ
−
e
−
i
ϕ
2
i
2
i
z
=
ξ
−
1
ξ
0
=
ξ
2
−
2
i
z
ξ
−
1
ξ
=
i
z
±
1
−
z
2
ϕ
=
−
i
ln
(
i
z
±
1
−
z
2
)
{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}
(the positive branch is chosen)
ϕ
=
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
{\displaystyle \phi =\arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)}
Color wheel graphs of inverse trigonometric functions in the complex plane
arcsin
(
z
)
{\displaystyle \arcsin(z)}
arccos
(
z
)
{\displaystyle \arccos(z)}
arctan
(
z
)
{\displaystyle \arctan(z)}
arccsc
(
z
)
{\displaystyle \operatorname {arccsc}(z)}
arcsec
(
z
)
{\displaystyle \operatorname {arcsec}(z)}
arccot
(
z
)
{\displaystyle \operatorname {arccot}(z)}
Expression as definite integrals [ sửa ] Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
arctan
(
x
)
=
∫
0
x
1
z
2
+
1
d
z
,
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
arcsec
(
x
)
=
∫
1
x
1
z
z
2
−
1
d
z
=
π
+
∫
−
x
−
1
1
z
z
2
−
1
d
z
,
x
≥
1
arccsc
(
x
)
=
∫
x
∞
1
z
z
2
−
1
d
z
=
∫
−
∞
−
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\int _{-\infty }^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\end{aligned}}}
When x equals 1, the integrals with limited domains are improper integrals , but still well-defined.
Similar to the sine and cosine functions, the inverse trigonometric functions can also be calculated using power series , as follows. For arcsine, the series can be derived by expanding its derivative,
1
1
−
z
2
{\textstyle {\tfrac {1}{\sqrt {1-z^{2}}}}}
binomial series , and integrating term by term (using the integral definition as above). The series for arctangent can similarly be derived by expanding its derivative
1
1
+
z
2
{\textstyle {\frac {1}{1+z^{2}}}}
geometric series , and applying the integral definition above (see Leibniz series ).
arcsin
(
z
)
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}
arctan
(
z
)
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq i,-i}
Series for the other inverse trigonometric functions can be given in terms of these according to the relationships given above. For example,
arccos
(
x
)
=
π
/
2
−
arcsin
(
x
)
{\displaystyle \arccos(x)=\pi /2-\arcsin(x)}
arccsc
(
x
)
=
arcsin
(
1
/
x
)
{\displaystyle \operatorname {arccsc}(x)=\arcsin(1/x)}
[ 1]
2
(
arcsin
(
x
2
)
)
2
=
∑
n
=
1
∞
x
2
n
n
2
(
2
n
n
)
.
{\displaystyle 2\left(\arcsin \left({\frac {x}{2}}\right)\right)^{2}=\sum _{n=1}^{\infty }{\frac {x^{2n}}{n^{2}{\binom {2n}{n}}}}.}
Leonhard Euler found a series for the arctangent that converges more quickly than its Taylor series :
arctan
(
z
)
=
z
1
+
z
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
z
2
(
2
k
+
1
)
(
1
+
z
2
)
.
{\displaystyle \arctan(z)={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}
[ 2] (The term in the sum for n = 0 is the empty product , so is 1.)
Alternatively, this can be expressed as
arctan
(
z
)
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
z
2
n
+
1
(
1
+
z
2
)
n
+
1
.
{\displaystyle \arctan(z)=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}
Another series for the arctangent function is given by
arctan
(
z
)
=
i
∑
n
=
1
∞
1
2
n
−
1
(
1
(
1
+
2
i
/
z
)
2
n
−
1
−
1
(
1
−
2
i
/
z
)
2
n
−
1
)
,
{\displaystyle \arctan(z)=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{(1+2i/z)^{2n-1}}}-{\frac {1}{(1-2i/z)^{2n-1}}}\right),}
where
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
imaginary unit .[ 3]
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Continued fractions for arctangent [ sửa ] Two alternatives to the power series for arctangent are these generalized continued fractions :
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
Indefinite integrals of inverse trigonometric functions [ sửa ] For real and complex values of z :
∫
arcsin
(
z
)
d
z
=
z
arcsin
(
z
)
+
1
−
z
2
+
C
∫
arccos
(
z
)
d
z
=
z
arccos
(
z
)
−
1
−
z
2
+
C
∫
arctan
(
z
)
d
z
=
z
arctan
(
z
)
−
1
2
ln
(
1
+
z
2
)
+
C
∫
arccot
(
z
)
d
z
=
z
arccot
(
z
)
+
1
2
ln
(
1
+
z
2
)
+
C
∫
arcsec
(
z
)
d
z
=
z
arcsec
(
z
)
−
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
∫
arccsc
(
z
)
d
z
=
z
arccsc
(
z
)
+
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}
For real x ≥ 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
For all real x not between -1 and 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\end{aligned}}}
The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions :
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
arcosh
(
|
x
|
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
arcosh
(
|
x
|
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {arcosh} (|x|)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {arcosh} (|x|)+C\\\end{aligned}}}
The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.
All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.
Using
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,dv=uv-\int v\,du}
integration by parts ), set
u
=
arcsin
(
x
)
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}}
Then
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
−
∫
x
1
−
x
2
d
x
,
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,dx,}
which by the simple substitution
w
=
1
−
x
2
,
d
w
=
−
2
x
d
x
{\displaystyle w=1-x^{2},\ dw=-2x\,dx}
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
These functions may also be expressed using complex logarithms . This extends their domains to the complex plane in a natural fashion. The following identities for principal values of the functions hold everywhere that they are defined, even on their branch cuts.
arcsin
(
z
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
=
i
ln
(
1
−
z
2
−
i
z
)
=
arccsc
(
1
z
)
arccos
(
z
)
=
−
i
ln
(
i
1
−
z
2
+
z
)
=
π
2
−
arcsin
(
z
)
=
arcsec
(
1
z
)
arctan
(
z
)
=
−
i
2
ln
(
i
−
z
i
+
z
)
=
−
i
2
ln
(
1
+
i
z
1
−
i
z
)
=
arccot
(
1
z
)
arccot
(
z
)
=
−
i
2
ln
(
z
+
i
z
−
i
)
=
−
i
2
ln
(
i
z
−
1
i
z
+
1
)
=
arctan
(
1
z
)
arcsec
(
z
)
=
−
i
ln
(
i
1
−
1
z
2
+
1
z
)
=
π
2
−
arccsc
(
z
)
=
arccos
(
1
z
)
arccsc
(
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
=
i
ln
(
1
−
1
z
2
−
i
z
)
=
arcsin
(
1
z
)
{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}
Because all of the inverse trigonometric functions output an angle of a right triangle, they can be generalized by using Euler's formula to form a right triangle in the complex plane. Algebraically, this gives us:
c
e
i
θ
=
c
cos
(
θ
)
+
i
c
sin
(
θ
)
{\displaystyle ce^{i\theta }=c\cos(\theta )+ic\sin(\theta )}
or
c
e
i
θ
=
a
+
i
b
{\displaystyle ce^{i\theta }=a+ib}
where
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
θ
{\displaystyle \theta }
e
ln
(
c
)
+
i
θ
=
a
+
i
b
ln
c
+
i
θ
=
ln
(
a
+
i
b
)
θ
=
Im
(
ln
(
a
+
i
b
)
)
{\displaystyle {\begin{aligned}e^{\ln(c)+i\theta }&=a+ib\\\ln c+i\theta &=\ln(a+ib)\\\theta &=\operatorname {Im} \left(\ln(a+ib)\right)\end{aligned}}}
or
θ
=
−
i
ln
(
a
+
i
b
c
)
{\displaystyle \theta =-i\ln \left({\frac {a+ib}{c}}\right)}
Simply taking the imaginary part works for any real-valued
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
ln
(
a
+
b
i
)
{\displaystyle \ln(a+bi)}
c
{\displaystyle c}
z
{\displaystyle z}
Pythagorean Theorem relation
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
The table below shows the values of a, b, and c for each of the inverse trig functions and the equivalent expressions for
θ
{\displaystyle \theta }
a
b
c
−
i
ln
(
a
+
i
b
c
)
θ
θ
a
,
b
∈
R
arcsin
(
z
)
1
−
z
2
z
1
−
i
ln
(
1
−
z
2
+
i
z
1
)
=
−
i
ln
(
1
−
z
2
+
i
z
)
Im
(
ln
(
1
−
z
2
+
i
z
)
)
arccos
(
z
)
z
1
−
z
2
1
−
i
ln
(
z
+
i
1
−
z
2
1
)
=
−
i
ln
(
z
+
z
2
−
1
)
Im
(
ln
(
z
+
z
2
−
1
)
)
arctan
(
z
)
1
z
1
+
z
2
−
i
ln
(
1
+
i
z
1
+
z
2
)
=
−
i
ln
(
1
+
i
z
1
+
z
2
)
Im
(
ln
(
1
+
i
z
)
)
arccot
(
z
)
z
1
z
2
+
1
−
i
ln
(
z
+
i
z
2
+
1
)
=
−
i
ln
(
z
+
i
z
2
+
1
)
Im
(
ln
(
z
+
i
)
)
arcsec
(
z
)
1
z
2
−
1
z
−
i
ln
(
1
+
i
z
2
−
1
z
)
=
−
i
ln
(
1
z
+
1
z
2
−
1
)
Im
(
ln
(
1
z
+
1
z
2
−
1
)
)
arccsc
(
z
)
z
2
−
1
1
z
−
i
ln
(
z
2
−
1
+
i
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
Im
(
ln
(
1
−
1
z
2
+
i
z
)
)
{\displaystyle {\begin{aligned}&a&&b&&c&&-i\ln \left({\frac {a+ib}{c}}\right)&&\theta &&\theta _{a,b\in \mathbb {R} }\\\arcsin(z)\ \ &{\sqrt {1-z^{2}}}&&z&&1&&-i\ln \left({\frac {{\sqrt {1-z^{2}}}+iz}{1}}\right)&&=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-z^{2}}}+iz\right)\right)\\\arccos(z)\ \ &z&&{\sqrt {1-z^{2}}}&&1&&-i\ln \left({\frac {z+i{\sqrt {1-z^{2}}}}{1}}\right)&&=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)&&\operatorname {Im} \left(\ln \left(z+{\sqrt {z^{2}-1}}\right)\right)\\\arctan(z)\ \ &1&&z&&{\sqrt {1+z^{2}}}&&-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&=-i\ln \left({\frac {1+iz}{\sqrt {1+z^{2}}}}\right)&&\operatorname {Im} \left(\ln \left(1+iz\right)\right)\\\operatorname {arccot}(z)\ \ &z&&1&&{\sqrt {z^{2}+1}}&&-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&=-i\ln \left({\frac {z+i}{\sqrt {z^{2}+1}}}\right)&&\operatorname {Im} \left(\ln \left(z+i\right)\right)\\\operatorname {arcsec}(z)\ \ &1&&{\sqrt {z^{2}-1}}&&z&&-i\ln \left({\frac {1+i{\sqrt {z^{2}-1}}}{z}}\right)&&=-i\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)&&\operatorname {Im} \left(\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right)\right)\\\operatorname {arccsc}(z)\ \ &{\sqrt {z^{2}-1}}&&1&&z&&-i\ln \left({\frac {{\sqrt {z^{2}-1}}+i}{z}}\right)&&=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&&\operatorname {Im} \left(\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)\right)\\\end{aligned}}}
In order to match the principal branch of the natural log and square root functions to the usual principal branch of the inverse trig functions, the particular form of the simplified formulation matters. The formulations given in the two rightmost columns assume
Im
(
ln
z
)
∈
(
−
π
,
π
]
{\displaystyle \operatorname {Im} \left(\ln z\right)\in (-\pi ,\pi ]}
Re
(
z
)
≥
0
{\displaystyle \operatorname {Re} \left({\sqrt {z}}\right)\geq 0}
Im
(
ln
z
)
∈
[
0
,
2
π
)
{\displaystyle \operatorname {Im} \left(\ln z\right)\in [0,2\pi )}
Im
(
z
)
≥
0
{\displaystyle \operatorname {Im} \left({\sqrt {z}}\right)\geq 0}
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
Re
(
θ
)
>
π
{\displaystyle \operatorname {Re} (\theta )>\pi }
In this sense, all of the inverse trig functions can be thought of as specific cases of the complex-valued log function. Since these definition work for any complex-valued
z
{\displaystyle z}
hyperbolic angles as outputs and can be used to further define the inverse hyperbolic functions . Elementary proofs of the relations may also proceed via expansion to exponential forms of the trigonometric functions.
sin
(
ϕ
)
=
z
ϕ
=
arcsin
(
z
)
{\displaystyle {\begin{aligned}\sin(\phi )&=z\\\phi &=\arcsin(z)\end{aligned}}}
Using the exponential definition of sine , and letting
ξ
=
e
i
ϕ
,
{\displaystyle \xi =e^{i\phi },}
z
=
e
i
ϕ
−
e
−
i
ϕ
2
i
2
i
z
=
ξ
−
1
ξ
0
=
ξ
2
−
2
i
z
ξ
−
1
ξ
=
i
z
±
1
−
z
2
ϕ
=
−
i
ln
(
i
z
±
1
−
z
2
)
{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}
(the positive branch is chosen)
ϕ
=
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
{\displaystyle \phi =\arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)}
Color wheel graphs of inverse trigonometric functions in the complex plane
arcsin
(
z
)
{\displaystyle \arcsin(z)}
arccos
(
z
)
{\displaystyle \arccos(z)}
arctan
(
z
)
{\displaystyle \arctan(z)}
arccsc
(
z
)
{\displaystyle \operatorname {arccsc}(z)}
arcsec
(
z
)
{\displaystyle \operatorname {arcsec}(z)}
arccot
(
z
)
{\displaystyle \operatorname {arccot}(z)}
▲ Chú thích có lỗi Thẻ <ref> sai; không có nội dung trong thẻ ref có tên Borwein_2004; $2 ▲ Bản mẫu:Citation ▲ Bản mẫu:Citation
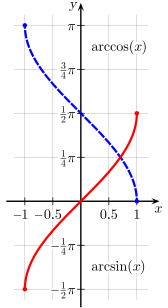
















































![{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec43798232f580abb074cf15f3d77692edd36af0)

![{\displaystyle {\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecb0a376d9148e3cf65ea6e6ed5fb37752a581c7)




![{\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ if }}-1<x\leq 1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dd6a9370a877ca5e198e28b7582bd06b377bdc3)










![{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0f778db7f760db059cf12f13ee5c2bf239fbb2f)









![{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e2dde92bb82231c4326e45ce8b50e7298688bb)








![{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13b511be341b52fcd0c0660f3a4b1e5a164bfcb1)












![{\displaystyle \operatorname {Im} \left(\ln z\right)\in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/781cef7f2317c18794eeaaddeef4073aadd51b75)







![{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed03e8cf773fa44cc78823d65f7d82f41276fb96)






