Số đại số được phân loai thành các loại số dưới đây
Loai số loại số Ký hiệu Thí dụ
Số tự nhiên
N
{\displaystyle N}
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle 1,2,3,4,5,6,7,8,9}
Số chẳn
2
N
{\displaystyle 2N}
2
,
4
,
6
,
8
{\displaystyle 2,4,6,8}
Số lẻ
2
N
+
1
{\displaystyle 2N+1}
1
,
3
,
5
,
7
,
9
{\displaystyle 1,3,5,7,9}
Số nguyên tố
P
{\displaystyle P}
1
,
3
,
5
,
7
{\displaystyle 1,3,5,7}
Phân số
c
=
a
b
{\displaystyle c={\frac {a}{b}}}
1
2
{\displaystyle {\frac {1}{2}}}
Số thập phân
a
=
0.
a
b
c
d
{\displaystyle a=0.abcd}
0.
a
b
c
d
{\displaystyle 0.abcd}
Số hửu tỉ
a
=
0.
a
a
a
a
a
a
{\displaystyle a=0.aaaaaa}
0.33333
{\displaystyle 0.33333}
Số vô tỉ
a
=
0.
a
b
c
d
e
f
{\displaystyle a=0.abcdef}
0.1345
{\displaystyle 0.1345}
Số nguyên
I
=
+
I
,
0
,
−
I
{\displaystyle I=+I,0,-I}
−
1
,
−
2
,
−
3
,
−
4
,
−
5
,
−
6
,
−
7
,
−
8
,
−
9
,
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle -1,-2,-3,-4,-5,-6,-7,-8,-9,0,1,2,3,4,5,6,7,8,9}
Số phức
Z
=
a
±
j
b
{\displaystyle Z=a\pm jb}
Z
=
2
±
j
3
{\displaystyle Z=2\pm j3}
Số thực
a
{\displaystyle a}
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle 1,2,3,4,5,6,7,8,9}
Số ảo
j
=
−
1
{\displaystyle j={\sqrt {-1}}}
j
5
{\displaystyle j5}
Toán Ký Hiệu Công Thức Định Nghỉa
Toán cộng
+
{\displaystyle +}
A
+
B
{\displaystyle A+B}
Toán Cộng hai số đại số
Toán trừ
−
{\displaystyle -}
A
−
B
{\displaystyle A-B}
Toán Trừ hai số đại số
Toán nhân
x
{\displaystyle x}
A
×
B
{\displaystyle A\times B}
Toán Nhân hai số đại số
Toán chia
/
{\displaystyle /}
A
/
B
{\displaystyle A/B}
Toán Chia hai số đại số
Toán lũy thừa
a
n
{\displaystyle a^{n}}
a
n
=
a
×
a
×
a
.
.
.
{\displaystyle a^{n}=a\times a\times a...}
Toán tìm tích n lần của chính số nhân
Toán căn
{\displaystyle {\sqrt {}}}
a
=
b
{\displaystyle {\sqrt {a}}=b}
b
n
=
a
{\displaystyle b^{n}=a}
Toán lủy thừa nghịch
Toán log
L
o
g
,
L
n
{\displaystyle Log,Ln}
L
o
g
a
=
b
{\displaystyle Loga=b}
10
b
=
a
{\displaystyle 10^{b}=a}
Toán Toán lủy thừa nghịch của một lủy thừa
Mọi số đếm đều là số tự nhiên có ký hiệu
N
{\displaystyle N}
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle 1,2,3,4,5,6,7,8,9}
Mọi số chẳn đều chia hết cho 2 không có số dư và có
Ký hiệu
2
N
{\displaystyle 2N}
Thí dụ
2
,
4
,
6
,
8
{\displaystyle 2,4,6,8}
Mọi số lẻ không chia hết cho 2 và có số dư bằng 1 và có
Ký hiệu
2
N
+
1
{\displaystyle 2N+1}
Thí dụ
1
,
3
,
5
,
7
,
9
{\displaystyle 1,3,5,7,9}
Mọi số nguyên tố đều chia hết cho 1 và cho chính nó và có
Ký hiệu
P
{\displaystyle P}
Thí dụ
1
,
3
,
5
,
7
{\displaystyle 1,3,5,7}
a
b
{\displaystyle {\frac {a}{b}}}
1
2
{\displaystyle {\frac {1}{2}}}
[ sửa ] Phân số đại diện cho một tỉ lệ của 2 đại lượng cho biết thành phần của một đại lượng so với một đại lượng khác
Thí dụ
1 phần 2 cái bánh được viết là
1
2
{\displaystyle {\frac {1}{2}}}
1 phần 3 cái bánh được viết là
1
3
{\displaystyle {\frac {1}{3}}}
1 phần n cái bánh được viết là
1
n
{\displaystyle {\frac {1}{n}}}
Khi so sánh 2 đại lượng đại số
a
b
=
1
{\displaystyle {\frac {a}{b}}=1}
a
=
b
{\displaystyle a=b}
a
b
>
1
{\displaystyle {\frac {a}{b}}>1}
a
>
b
{\displaystyle a>b}
a
b
<
1
{\displaystyle {\frac {a}{b}}<1}
a
<
b
{\displaystyle a<b}
[ sửa ]
a
b
=
a
/
b
{\displaystyle {\frac {a}{b}}=a/b}
Khi chia hết, được một thương só và không có số dư
a
b
=
c
{\displaystyle {\frac {a}{b}}=c}
a
c
=
b
{\displaystyle ac=b}
Khi không chia hết , được một thương só và có số dư
a
b
=
c
{\displaystyle {\frac {a}{b}}=c}
a
c
+
r
=
b
{\displaystyle ac+r=b}
Số thập phân, số có dạng 0.abcd
1
2
=
0.5
{\displaystyle {\frac {1}{2}}=0.5}
1
4
=
0.25
{\displaystyle {\frac {1}{4}}=0.25}
1
8
=
0.125
{\displaystyle {\frac {1}{8}}=0.125}
Số hửu tỉ , số thập phân lặp lại
1
3
=
0.333333...
{\displaystyle {\frac {1}{3}}=0.333333...}
Số vô tỉ , số thập phân không lặp lại
π
=
3.1415...
{\displaystyle \pi =3.1415...}
Hổn số là một phân số có giá trị lớn hơn 1 .
Thí dụ
a
b
c
{\displaystyle a{\frac {b}{c}}}
Chuyển đổi Hỗn số sang phân số được thực hiện như sau
a
b
c
=
a
+
b
c
=
a
c
+
b
c
{\displaystyle a{\frac {b}{c}}=a+{\frac {b}{c}}={\frac {ac+b}{c}}}
Phân số tối giản là phân số nhỏ nhứt không thể đơn giản nhỏ hơn được .
Thí dụ, phân số tối giản
1
2
{\displaystyle {\frac {1}{2}}}
2
4
{\displaystyle {\frac {2}{4}}}
5
10
{\displaystyle {\frac {5}{10}}}
a chia hết cho b khi
a
b
=
c
{\displaystyle {\frac {a}{b}}=c}
a
=
b
c
{\displaystyle a=bc}
a không chia hết cho b khi
a
b
=
c
{\displaystyle {\frac {a}{b}}=c}
a
=
b
c
+
r
{\displaystyle a=bc+r}
a
b
{\displaystyle {\frac {a}{b}}}
c
d
{\displaystyle {\frac {c}{d}}}
a
=
c
{\displaystyle a=c}
b
=
d
{\displaystyle b=d}
a
d
b
d
=
b
c
b
d
{\displaystyle {\frac {ad}{bd}}={\frac {bc}{bd}}}
a
d
=
b
c
{\displaystyle ad=bc}
a
b
>
c
d
{\displaystyle {\frac {a}{b}}>{\frac {c}{d}}}
a
b
<
c
d
{\displaystyle {\frac {a}{b}}<{\frac {c}{d}}}
a
b
+
c
d
=
a
d
+
b
c
b
d
{\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}}
a
b
−
c
d
=
a
d
−
b
c
b
d
{\displaystyle {\frac {a}{b}}-{\frac {c}{d}}={\frac {ad-bc}{bd}}}
a
b
×
c
d
=
a
c
b
d
{\displaystyle {\frac {a}{b}}\times {\frac {c}{d}}={\frac {ac}{bd}}}
a
b
/
c
d
=
a
b
×
d
c
=
a
d
b
c
{\displaystyle {\frac {a}{b}}/{\frac {c}{d}}={\frac {a}{b}}\times {\frac {d}{c}}={\frac {ad}{bc}}}
Mọi số tự nhiên có giá trị bằng không được gọi là số nguyên không, lớn hơn không được gọi là số nguyên dương , nhỏ hơn không được gọi là số nguyên âm
Số nguyên Số nguyên dương Số nguyên không Số nguyên âm
I
+I>0
I=0
-I <0
−
1
,
−
2
,
−
3
,
−
4
,
−
5
,
−
6
,
−
7
,
−
8
,
−
9
,
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
{\displaystyle -1,-2,-3,-4,-5,-6,-7,-8,-9,0,1,2,3,4,5,6,7,8,9}
Toán cộng
0
+
±
a
=
±
a
{\displaystyle 0+\pm a=\pm a}
Toán trừ
0
−
±
a
=
∓
a
{\displaystyle 0-\pm a=\mp a}
Toán nhân
0
×
±
a
=
0
{\displaystyle 0\times \pm a=0}
toán chia
0
/
±
a
=
0
{\displaystyle 0/\pm a=0}
Toán cộng
a
+
a
=
2
a
{\displaystyle a+a=2a}
a
+
0
=
a
{\displaystyle a+0=a}
a
−
a
=
0
{\displaystyle a-a=0}
a
−
0
=
a
{\displaystyle a-0=a}
a
×
a
=
a
2
{\displaystyle a\times a=a^{2}}
a
×
1
=
a
{\displaystyle a\times 1=a}
a
×
0
=
0
{\displaystyle a\times 0=0}
a
/
a
=
1
{\displaystyle a/a=1}
a
/
1
=
a
{\displaystyle a/1=a}
a
/
0
=
00
{\displaystyle a/0=00}
a
0
=
1
{\displaystyle a^{0}=1}
a
n
=
a
×
a
×
a
.
.
.
{\displaystyle a^{n}=a\times a\times a...}
a
−
n
=
1
a
n
{\displaystyle a^{-n}={\frac {1}{a^{n}}}}
a
1
n
=
n
a
{\displaystyle a^{\frac {1}{n}}=n{\sqrt {a}}}
n
a
=
a
1
n
{\displaystyle n{\sqrt {a}}=a^{\frac {1}{n}}}
0
=
E
r
r
o
r
{\displaystyle {\sqrt {0}}=Error}
1
=
1
{\displaystyle {\sqrt {1}}=1}
−
1
=
j
{\displaystyle {\sqrt {-1}}=j}
a
n
m
=
a
m
n
=
a
1
m
n
{\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}}
a
b
n
=
a
n
b
n
{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}}
a
b
n
{\displaystyle {\sqrt[{n}]{ab}}}
a
n
{\displaystyle {\sqrt[{n}]{a}}}
b
n
{\displaystyle {\sqrt[{n}]{b}}}
a
a
=
a
2
×
a
=
a
3
{\displaystyle a{\sqrt {a}}={\sqrt {a^{2}\times a}}={\sqrt {a^{3}}}}
a
n
=
a
a
n
−
2
{\displaystyle {\sqrt {a^{n}}}=a{\sqrt {a^{n-2}}}}
L
o
g
10
n
=
n
{\displaystyle Log10^{n}=n}
log
b
(
a
c
)
=
log
b
(
a
)
+
log
b
(
c
)
{\displaystyle \log _{b}(ac)=\log _{b}(a)+\log _{b}(c)\ }
log
b
(
a
/
c
)
=
log
b
(
a
)
−
log
b
(
c
)
{\displaystyle \log _{b}(a/c)=\log _{b}(a)-\log _{b}(c)\ }
log
b
(
b
a
)
=
a
{\displaystyle \log _{b}(b^{a})=a\ }
log
b
(
a
)
=
log
d
(
a
)
log
d
(
b
)
{\displaystyle \log _{b}(a)={\frac {\log _{d}(a)}{\log _{d}(b)}}}
d
>
0
,
d
<>
1
{\displaystyle d>0,d<>1}
log
b
(
y
a
)
=
a
log
b
(
y
)
{\displaystyle \log _{b}(y^{a})=a\log _{b}(y)\ }
−
a
+
(
−
a
)
=
−
2
a
{\displaystyle -a+(-a)=-2a}
−
a
+
0
=
−
a
{\displaystyle -a+0=-a}
−
a
−
(
−
a
)
=
0
{\displaystyle -a-(-a)=0}
−
a
−
0
=
−
a
{\displaystyle -a-0=-a}
−
a
×
(
−
a
)
=
a
2
{\displaystyle -a\times (-a)=a^{2}}
−
a
×
1
=
−
a
{\displaystyle -a\times 1=-a}
−
a
×
0
=
0
{\displaystyle -a\times 0=0}
−
a
/
(
−
a
)
=
1
{\displaystyle -a/(-a)=1}
−
a
/
1
=
−
a
{\displaystyle -a/1=-a}
−
a
/
0
=
00
{\displaystyle -a/0=00}
(
−
a
)
0
=
1
{\displaystyle (-a)^{0}=1}
(
−
a
)
n
=
−
a
n
{\displaystyle (-a)^{n}=-a^{n}}
n
=
2
m
+
1
{\displaystyle n=2m+1}
(
−
a
)
n
=
a
n
{\displaystyle (-a)^{n}=a^{n}}
n
=
2
m
{\displaystyle n=2m}
−
a
=
±
j
a
{\displaystyle {\sqrt {-a}}=\pm j{\sqrt {a}}}
Số phức đại diện cho tổng hay hiệu của một số thực và một số ảo
Z
=
a
+
j
b
{\displaystyle Z=a+jb}
Z
=
a
−
j
b
{\displaystyle Z=a-jb}
Ký hiệu tổng quát
Z
=
a
±
j
b
{\displaystyle Z=a\pm jb}
Z
=
2
±
j
3
{\displaystyle Z=2\pm j3}
Số phức thuận
Z
=
(
a
+
i
b
)
{\displaystyle Z=(a+ib)}
Z
∠
θ
{\displaystyle Z\angle \theta }
Z
=
Z
(
cos
θ
+
i
sin
θ
)
{\displaystyle Z=Z(\cos \theta +i\sin \theta )}
Z
e
j
θ
{\displaystyle Ze^{j\theta }}
Số phức nghịch
Z
=
(
a
−
i
b
)
{\displaystyle Z=(a-ib)}
Z
∠
−
θ
{\displaystyle Z\angle -\theta }
Z
=
Z
(
cos
θ
−
i
sin
θ
)
{\displaystyle Z=Z(\cos \theta -i\sin \theta )}
Z
e
−
j
θ
{\displaystyle Ze^{-j\theta }}
+
2
a
{\displaystyle 2a}
Z
(
∠
θ
+
∠
−
θ
)
{\displaystyle Z(\angle \theta +\angle -\theta )}
2
Z
cos
θ
{\displaystyle 2Z\cos \theta }
Z
(
e
j
θ
+
e
−
j
θ
)
{\displaystyle Z(e^{j\theta }+e^{-j\theta })}
-
i
2
b
{\displaystyle i2b}
Z
(
∠
θ
−
∠
−
θ
)
{\displaystyle Z(\angle \theta -\angle -\theta )}
i
2
Z
sin
θ
{\displaystyle i2Z\sin \theta }
Z
(
e
j
θ
−
e
−
j
θ
)
{\displaystyle Z(e^{j\theta }-e^{-j\theta })}
x
a
2
−
b
2
{\displaystyle a^{2}-b^{2}}
Z
2
∠
0
{\displaystyle Z^{2}\angle 0}
Z
2
(
cos
2
θ
−
sin
2
θ
)
{\displaystyle Z^{2}(\cos ^{2}\theta -\sin ^{2}\theta )}
Z
2
e
{\displaystyle Z^{2}e}
/
a
2
−
b
2
a
−
i
b
{\displaystyle {\frac {a^{2}-b^{2}}{a-ib}}}
1
∠
2
θ
{\displaystyle 1\angle 2\theta }
cos
2
θ
−
sin
2
θ
(
cos
θ
−
i
sin
θ
)
{\displaystyle {\frac {\cos ^{2}\theta -\sin ^{2}\theta }{(\cos \theta -i\sin \theta )}}}
e
j
2
θ
{\displaystyle e^{j2\theta }}
(
)
n
{\displaystyle ()^{n}}
(
a
+
i
b
)
n
{\displaystyle (a+ib)^{n}}
Định luật De Moive
(
Z
∠
θ
)
n
=
Z
n
∠
n
θ
{\displaystyle (Z\angle \theta )^{n}=Z^{n}\angle n\theta }
[
e
j
θ
]
n
=
e
j
n
θ
{\displaystyle [e^{j\theta }]^{n}=e^{jn\theta }}
±
j
b
{\displaystyle \pm jb}
Với
j
=
−
1
{\displaystyle j={\sqrt {-1}}}
±
5
j
{\displaystyle \pm 5j}
a
{\displaystyle a}
Dải Số là một chuổi số có định dạng . Thí dụ
Dải số của các số tự nhiên .
1
,
2
,
3
,
4
,
5
,
.
.
.
.
,
n
{\displaystyle 1,2,3,4,5,....,n}
Dải số của các số tự nhiên chẳn .
2
,
4
,
6
,
8
,
10
,
.
.
.
,
2
n
{\displaystyle 2,4,6,8,10,...,2n}
Dải số của các số tự nhiên lẻ .
1
,
3
,
5
,
7
,
.
.
.
,
2
n
+
1
{\displaystyle 1,3,5,7,...,2n+1}
Tổng số một phép toán giải tích tìm tổng của một dải số như sau
s
=
1
+
2
+
3
+
.
.
.
+
n
{\displaystyle s=1+2+3+...+n}
Tổng dải số có ký hiệu
∑
{\displaystyle \sum }
Tổng của dải số từ 1 đến n có thể viết như sau
S
n
=
∑
i
=
1
n
a
i
=
1
+
2
+
⋯
+
n
=
k
(
1
+
n
)
{\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}=1+2+\cdots +n=k(1+n)}
[ sửa ] Tổng chuổi số cấp số cộng có dạng tổng quát
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}
∑
k
=
0
∞
[
a
+
(
n
−
1
)
d
]
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
=
n
2
(
2
a
+
(
n
−
1
)
d
)
{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}
S
=
a
+
(
a
+
d
)
+
(
a
+
2
d
)
+
.
.
.
+
[
a
+
(
n
−
1
)
d
]
{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}
S
=
[
a
+
(
n
−
1
)
d
]
+
.
.
.
+
(
n
−
1
)
d
]
+
a
{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}
2
S
=
[
2
a
+
(
n
−
1
)
d
]
n
{\displaystyle 2S=[2a+(n-1)d]n}
S
=
[
2
a
+
(
n
−
1
)
d
]
n
2
{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}
Dải số cấp số cộng có dạng tổng quát
1
,
2
,
3
,
.
.
.9
{\displaystyle 1,2,3,...9}
Tổng số của dải số
1
+
2
+
3
+
4
+
5
+
.
.
.9
=
50
{\displaystyle 1+2+3+4+5+...9=50}
Cách giải
S
=
(
1
+
9
)
+
(
2
+
8
)
+
(
3
+
7
)
+
(
4
+
6
)
+
(
5
+
5
)
=
10
(
5
)
=
50
{\displaystyle S=(1+9)+(2+8)+(3+7)+(4+6)+(5+5)=10(5)=50}
[ sửa ] Tổng chuổi số cấp số nhân có dạng tổng quát
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
∑
k
=
0
∞
(
a
r
k
)
{\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}=\sum _{k=0}^{\infty }(ar^{k})}
∑
k
=
0
∞
(
a
r
k
)
=
a
+
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
…
+
a
r
n
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle \sum _{k=0}^{\infty }(ar^{k})=a+ar+ar^{2}+ar^{3}+ar^{4}+\ldots +ar^{n}={\frac {a(1-r^{n})}{1-r}}}
S
=
a
+
a
r
+
a
r
2
+
a
r
3
+
.
.
.
+
a
r
n
−
1
{\displaystyle S=a+ar+ar^{2}+ar^{3}+...+ar^{n-1}}
r
S
=
a
r
+
a
r
2
+
a
r
3
+
a
r
4
+
.
.
.
+
a
r
n
{\displaystyle rS=ar+ar^{2}+ar^{3}+ar^{4}+...+ar^{n}}
S
−
r
S
=
a
−
a
r
n
{\displaystyle S-rS=a-ar^{n}}
S
=
a
(
1
−
r
n
)
1
−
r
{\displaystyle S={\frac {a(1-r^{n})}{1-r}}}
S
=
a
1
−
r
{\displaystyle S={\frac {a}{1-r}}}
n
<
1
{\displaystyle n<1}
1
+
1.1
+
1.1
2
+
1.1
3
=
4
{\displaystyle 1+1.1+1.1^{2}+1.1^{3}=4}
1
+
1.2
+
1.2
2
+
1.2
3
=
1
+
2
+
4
+
8
=
15
{\displaystyle 1+1.2+1.2^{2}+1.2^{3}=1+2+4+8=15}
[ sửa ]
(
x
+
y
)
n
{\displaystyle (x+y)^{n}}
Công thức tổng quát lũy thừa n của một tổng
(
x
+
y
)
n
=
∑
r
=
0
n
(
n
r
)
x
r
y
n
−
r
{\displaystyle (x+y)^{n}=\sum _{r=0}^{n}{n \choose r}x^{r}y^{n-r}}
(
x
+
y
)
n
=
(
n
0
)
x
0
y
n
+
(
n
1
)
x
1
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
(
n
n
−
1
)
x
n
−
1
y
1
+
(
n
n
)
x
n
y
0
{\displaystyle (x+y)^{n}={n \choose 0}x^{0}y^{n}+{n \choose 1}x^{1}y^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+{n \choose {n-1}}x^{n-1}y^{1}+{n \choose n}x^{n}y^{0}}
(
x
+
y
)
n
=
y
n
+
n
x
y
n
−
1
+
(
n
2
)
x
2
y
n
−
2
+
⋯
+
(
n
n
−
2
)
x
n
−
2
y
2
+
n
x
n
−
1
y
+
x
n
{\displaystyle (x+y)^{n}=y^{n}+nxy^{n-1}+{n \choose 2}x^{2}y^{n-2}+\dots +{n \choose {n-2}}x^{n-2}y^{2}+nx^{n-1}y+x^{n}}
Với
(
n
r
)
=
n
!
r
!
(
n
−
r
)
!
{\displaystyle {n \choose r}={\frac {n!}{r!(n-r)!}}}
(
x
+
1
)
1
=
{\displaystyle (x+1)^{1}=}
1
x
+
1
{\displaystyle 1x+1}
(
x
+
1
)
2
=
{\displaystyle (x+1)^{2}=}
1
x
2
+
2
x
+
1
{\displaystyle 1x^{2}+2x+1}
(
x
+
1
)
3
=
{\displaystyle (x+1)^{3}=}
1
x
3
+
3
x
2
+
3
x
+
1
{\displaystyle 1x^{3}+3x^{2}+3x+1}
(
x
+
1
)
4
=
{\displaystyle (x+1)^{4}=}
1
x
4
+
4
x
3
+
6
x
2
+
4
x
+
1
{\displaystyle 1x^{4}+4x^{3}+6x^{2}+4x+1}
(
x
+
1
)
5
=
{\displaystyle (x+1)^{5}=}
1
x
5
+
5
x
4
+
10
x
3
+
10
x
2
+
5
x
+
1
{\displaystyle 1x^{5}+5x^{4}+10x^{3}+10x^{2}+5x+1}
[ sửa ] Từ trên , ta thấy hằng số trước biến số x tạo hình tam giác Pascal dưới đây
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
[ sửa ]
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
f
‴
(
a
)
3
!
(
x
−
a
)
3
+
⋯
=
∑
n
=
0
∞
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}
[ sửa ] Tổng chuổi số Fourier có dạng tổng quát tổng của sine and cosine như sau
s
N
(
x
)
=
a
0
⏞
A
0
/
2
+
∑
n
=
1
N
(
a
n
⏞
A
n
sin
(
ϕ
n
)
cos
(
2
π
n
x
P
)
+
b
n
⏞
A
n
cos
(
ϕ
n
)
sin
(
2
π
n
x
P
)
)
,
{\displaystyle {\begin{aligned}s_{N}(x)&=\overbrace {a_{0}} ^{A_{0}}/2+\sum _{n=1}^{N}\left(\overbrace {a_{n}} ^{A_{n}\sin(\phi _{n})}\cos \left({\tfrac {2\pi nx}{P}}\right)+\overbrace {b_{n}} ^{A_{n}\cos(\phi _{n})}\sin \left({\tfrac {2\pi nx}{P}}\right)\right),\\\end{aligned}}}
a
0
=
A
0
a
n
=
A
n
sin
(
ϕ
n
)
for
n
≥
1
b
n
=
A
n
cos
(
ϕ
n
)
for
n
≥
1
{\displaystyle {\begin{aligned}a_{0}&=A_{0}\\a_{n}&=A_{n}\sin(\phi _{n})&{\text{for }}n\geq 1\\b_{n}&=A_{n}\cos(\phi _{n})&{\text{for }}n\geq 1\end{aligned}}}
Giá trị hằng số a,b
a
n
=
2
P
∫
x
0
x
0
+
P
s
(
x
)
⋅
cos
(
2
π
n
x
P
)
d
x
for
n
≥
0
b
n
=
2
P
∫
x
0
x
0
+
P
s
(
x
)
⋅
sin
(
2
π
n
x
P
)
d
x
for
n
>
0
{\displaystyle {\begin{aligned}a_{n}&={\frac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot \cos \left({\tfrac {2\pi nx}{P}}\right)\ dx&{\text{for }}n\geq 0\\b_{n}&={\frac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot \sin \left({\tfrac {2\pi nx}{P}}\right)\ dx&{\text{for }}n>0\end{aligned}}}
[ sửa ]
s
N
(
x
)
=
∑
n
=
−
N
N
c
n
⋅
e
i
2
π
n
x
P
,
{\displaystyle {\begin{aligned}s_{N}(x)&=\sum _{n=-N}^{N}c_{n}\cdot e^{i{\tfrac {2\pi nx}{P}}},\end{aligned}}}
Với
c
n
≜
{
A
n
2
i
e
i
ϕ
n
=
1
2
(
a
n
−
i
b
n
)
for
n
>
0
1
2
A
0
=
1
2
a
0
for
n
=
0
−
A
−
n
2
i
e
−
i
ϕ
−
n
=
1
2
(
a
−
n
+
i
b
−
n
)
=
c
|
n
|
∗
for
n
<
0.
{\displaystyle c_{n}\ \triangleq \ {\begin{cases}{\frac {A_{n}}{2i}}e^{i\phi _{n}}={\frac {1}{2}}(a_{n}-ib_{n})&{\text{for }}n>0\\{\frac {1}{2}}A_{0}={\frac {1}{2}}a_{0}&{\text{for }}n=0\\{\frac {-A_{-n}}{2i}}e^{-i\phi _{-n}}={\frac {1}{2}}(a_{-n}+ib_{-n})=c_{|n|}^{*}&{\text{for }}n<0.\end{cases}}}
Giá trị hằng số c
c
n
=
1
P
∫
x
0
x
0
+
P
s
(
x
)
⋅
e
−
i
2
π
n
x
P
d
x
for
n
∈
N
{\displaystyle c_{n}={\frac {1}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\quad {\text{for }}n\in \mathbb {N} }
Sóng vuông Tổng chuổi số Fourier đại diện cho tổng chuổi số hàm số sóng sine
s
N
(
x
)
=
A
0
2
+
∑
n
=
1
N
A
n
⋅
sin
(
2
π
n
x
P
+
ϕ
n
)
,
for integer
N
≥
1.
{\displaystyle s_{N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}A_{n}\cdot \sin \left({\tfrac {2\pi nx}{P}}+\phi _{n}\right),\quad {\text{for integer}}\ N\ \geq \ 1.}
Biểu thức đại số tạo từ nhiều đơn thức đại số cùng , các ngoặc đơn kép cùng với các phép toán đại số . Thí dụ
(
2
x
+
3
y
)
+
6
x
/
2
{\displaystyle (2x+3y)+6x/2}
Với
Đơn thức đại số .
2
x
,
3
y
,
6
x
,
2
{\displaystyle 2x,3y,6x,2}
Dấu ngoặc đơn . ()
Toán đại số . +, / [ sửa ] Thí dụ
(
2
x
+
3
y
)
=
6
x
/
2
{\displaystyle (2x+3y)=6x/2}
Bình phương tổng 2 số đại số
(
a
+
b
)
2
=
(
a
+
b
)
(
a
+
b
)
=
a
2
+
a
b
+
a
b
+
b
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=(a+b)(a+b)=a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}}
Bình phương hiệu 2 số đại số
(
a
−
b
)
2
=
(
a
−
b
)
(
a
−
b
)
=
a
2
−
a
b
−
a
b
+
b
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=(a-b)(a-b)=a^{2}-ab-ab+b^{2}=a^{2}-2ab+b^{2}}
Tổng 2 bình phương ||
a
2
+
b
2
=
(
a
+
b
)
2
−
2
a
b
{\displaystyle a^{2}+b^{2}=(a+b)^{2}-2ab}
a
2
+
b
2
=
(
a
−
b
)
2
+
2
a
b
{\displaystyle a^{2}+b^{2}=(a-b)^{2}+2ab}
Hiệu 2 bình phương
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
Tổng 2 lập phương
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})}
Hiệu 2 lập phương
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}
[ sửa ] Thí dụ
(
2
x
+
3
y
)
>
6
x
/
2
{\displaystyle (2x+3y)>6x/2}
(
2
x
+
3
y
)
<
6
x
/
2
{\displaystyle (2x+3y)<6x/2}
[ sửa ] Thứ tự thực thi phép toán biểu thức đại số như sau
A
=
2
x
+
5
y
−
3
{\displaystyle A=2x+5y-3}
B
=
52
y
−
5
{\displaystyle B=52y-5}
A
+
B
=
(
2
x
+
5
y
−
3
)
+
(
52
y
−
5
)
=
2
x
+
(
5
y
+
52
y
)
+
(
−
3
−
5
)
=
2
x
+
57
y
−
8
{\displaystyle A+B=(2x+5y-3)+(52y-5)=2x+(5y+52y)+(-3-5)=2x+57y-8}
A
−
B
=
(
2
x
+
5
y
−
3
)
−
(
52
y
−
5
)
=
2
x
+
(
5
y
−
52
y
)
+
[
−
3
−
(
−
5
)
]
=
2
x
−
47
y
+
2
{\displaystyle A-B=(2x+5y-3)-(52y-5)=2x+(5y-52y)+[-3-(-5)]=2x-47y+2}
Hàm số là một biểu thức đại số được dùng trong việc biểu diển tương quan giửa 2 đại lương với nhau . Thí dụ như
y
=
2
x
+
5
{\displaystyle y=2x+5}
Mọi hàm số đều có một hay nhiều hơn một biến số
Mọi hàm số của một biến số
f
(
x
)
{\displaystyle f(x)}
y
=
2
x
{\displaystyle y=2x}
Hàm số 2 biến số
f
(
x
,
y
)
{\displaystyle f(x,y)}
r
2
=
x
2
+
y
2
{\displaystyle r^{2}=x^{2}+y^{2}}
f
(
r
,
θ
)
{\displaystyle f(r,\theta )}
Z
∠
θ
=
(
x
2
+
y
2
)
∠
t
a
n
−
1
y
x
{\displaystyle Z\angle \theta ={\sqrt {(}}x^{2}+y^{2})\angle tan^{-1}{\frac {y}{x}}}
Hàm số 3 biến số
f
(
x
,
y
,
z
)
{\displaystyle f(x,y,z)}
r
2
=
x
2
+
y
2
+
z
2
{\displaystyle r^{2}=x^{2}+y^{2}+z^{2}}
Hàm số bằng không
f
(
x
)
=
0
{\displaystyle f(x)=0}
Hàm số bằng hằng số không đổi
f
(
x
)
=
C
{\displaystyle f(x)=C}
Hàm số khác không
f
(
x
)
=
y
(
x
)
{\displaystyle f(x)=y(x)}
Dạng hàm số Công thức Thí dụ
Hàm số tuần hoàn (Periodic function)
f
(
x
)
=
f
(
x
+
T
)
{\displaystyle f(x)=f(x+T)}
s
i
n
x
=
s
i
n
(
x
+
k
2
π
)
{\displaystyle sinx=sin(x+k2\pi )}
Hàm số chẳn (Even function)
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
Hàm số lẽ (Odd function)
f
(
x
)
=
−
f
(
x
)
{\displaystyle f(x)=-f(x)}
y
(
x
)
=
−
y
(
x
)
{\displaystyle y(x)=-y(x)}
Hàm số nghịch đảo (Inverse function)
f
−
1
(
x
)
=
1
f
(
x
)
{\displaystyle f^{-1}(x)={\frac {1}{f(x)}}}
s
i
n
−
1
x
=
1
s
i
n
x
{\displaystyle sin^{-1}{x}={\frac {1}{sinx}}}
Hàm số trong hàm số (Composite function)
f
(
x
)
=
f
(
g
(
x
)
)
{\displaystyle f(x)=f(g(x))}
Hàm số nhiều biến số (Parametric function)
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Hàm số tương quan/]] (Recursive function)
Hàm số chia/]] (Rational function)
Q
(
x
)
=
N
(
x
)
M
(
x
)
−
R
(
x
)
{\displaystyle Q(x)={\frac {N(x)}{M(x)}}-R(x)}
[ sửa ]
Dạng hàm số Công thức Thí dụ
y
=
y
o
+
Z
(
x
−
x
o
)
{\displaystyle y=y_{o}+Z(x-x_{o})}
y
=
a
x
+
b
{\displaystyle y=ax+b}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
(
Z
Z
)
2
=
(
X
Z
)
2
+
(
Y
Z
)
2
{\displaystyle ({\frac {Z}{Z}})^{2}=({\frac {X}{Z}})^{2}+({\frac {Y}{Z}})^{2}}
1
=
c
o
s
2
+
s
i
n
2
{\displaystyle 1=cos^{2}+sin^{2}}
1
=
s
e
c
2
+
t
a
n
2
{\displaystyle 1=sec^{2}+tan^{2}}
1
=
c
s
c
2
+
c
o
t
2
{\displaystyle 1=csc^{2}+cot^{2}}
y
=
a
x
n
{\displaystyle y=ax^{n}}
y
(
x
)
=
L
o
g
x
{\displaystyle y(x)=Logx}
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
s
e
c
θ
=
1
X
{\displaystyle sec\theta ={\frac {1}{X}}}
c
s
c
θ
=
1
Y
{\displaystyle csc\theta ={\frac {1}{Y}}}
t
a
n
θ
=
Y
X
{\displaystyle tan\theta ={\frac {Y}{X}}}
c
o
t
θ
=
X
Y
{\displaystyle cot\theta ={\frac {X}{Y}}}
[ sửa ] Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
+
.
.
.
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
+
.
.
.
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}+...=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}+...}
Chứng minh Khi x=0
f
(
0
)
=
a
0
{\displaystyle f(0)=a_{0}}
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
f
′
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
4
a
4
x
3
{\displaystyle f^{'}(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+4a_{4}x^{3}}
f
′
(
0
)
=
a
1
{\displaystyle f^{'}(0)=a_{1}}
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
f
″
(
x
)
=
2
a
2
+
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
a
4
x
2
+
(
5
)
(
4
)
a
5
x
3
{\displaystyle f^{''}(x)=2a_{2}+(3)(2)a_{3}x+(4)(3)a_{4}x^{2}+(5)(4)a_{5}x^{3}}
f
″
(
0
)
=
2
a
2
{\displaystyle f^{''}(0)=2a_{2}}
a
2
=
f
″
(
0
)
2
{\displaystyle a_{2}={\frac {f^{''}(0)}{2}}}
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
f
‴
(
x
)
=
(
3
)
(
2
)
a
3
x
+
(
4
)
(
3
)
(
2
)
a
4
x
+
(
5
)
(
4
)
(
3
)
a
5
x
2
{\displaystyle f^{'''}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_{5}x^{2}}
f
‴
(
0
)
=
(
3
)
(
2
)
a
3
{\displaystyle f^{'''}(0)=(3)(2)a_{3}}
a
3
=
f
‴
(
0
)
3
!
{\displaystyle a_{3}={\frac {f^{'''}(0)}{3!}}}
Thế
a
0
,
a
−
1
,
a
−
2
{\displaystyle a_{0},a-1,a-2}
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
3
+
a
4
x
4
{\displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{3}+a_{4}x^{4}}
f
(
x
)
=
f
(
0
)
+
f
′
x
(
0
)
+
f
″
(
0
)
2
!
+
f
‴
(
0
)
3
!
{\displaystyle f(x)=f(0)+f^{'}x(0)+{\frac {f^{''}(0)}{2!}}+{\frac {f^{'''}(0)}{3!}}}
Thí dụ
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f(0)=\sin(0)=0}
f
″
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{''}(x)=-\sin(x)}
f
″
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{''}(0)=-\sin(0)=0}
f
‴
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{'''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
sin
(
x
)
=
0
+
x
(
1
)
+
x
2
2
!
(
0
)
+
x
3
3
!
(
−
1
)
+
x
5
5
!
(
1
)
=
x
−
x
3
3
!
+
x
5
5
!
{\displaystyle \sin(x)=0+x(1)+{\frac {x^{2}}{2!}}(0)+{\frac {x^{3}}{3!}}(-1)+{\frac {x^{5}}{5!}}(1)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
x
)
=
cos
(
x
)
{\displaystyle f(x)=\cos(x)}
f
(
0
)
=
cos
(
0
)
=
1
{\displaystyle f(0)=\cos(0)=1}
f
′
(
x
)
=
−
sin
(
x
)
{\displaystyle f^{'}(x)=-\sin(x)}
f
′
(
0
)
=
−
sin
(
0
)
=
0
{\displaystyle f^{'}(0)=-\sin(0)=0}
f
″
(
x
)
=
−
cos
(
x
)
{\displaystyle f^{''}(x)=-\cos(x)}
f
‴
(
0
)
=
−
cos
(
0
)
=
−
1
{\displaystyle f^{'''}(0)=-\cos(0)=-1}
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f^{''''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
f
‴
(
x
)
=
sin
(
x
)
{\displaystyle f^{'''}(x)=\sin(x)}
f
‴
(
0
)
=
sin
(
0
)
=
0
{\displaystyle f^{'''}(0)=\sin(0)=0}
cos
(
x
)
=
1
+
x
(
0
)
+
x
2
2
!
(
−
1
)
+
x
3
3
!
(
0
)
+
x
4
4
!
(
1
)
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
{\displaystyle \cos(x)=1+x(0)+{\frac {x^{2}}{2!}}(-1)+{\frac {x^{3}}{3!}}(0)+{\frac {x^{4}}{4!}}(1)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}}
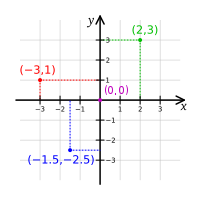
Đồ Thị là một cách hiển thị Tọa độ của một điểm trên một mặt phẳng . Có hai loại đồ thị Đồ Thị điểm XY và Đồ Thị điểm Rθ
Tương quan giửa 2 đại lượng x, y biểu thị bằng hàm sô
y
=
x
{\displaystyle y=x}
Lập bảng tương quan giửa hai giá trị x và y
x -2
-1
0
1
2
y = x -2
-1
0
1
2
Đặt điểm (x,y) trên đồ thi x-y ta có Đồ thị hàm số đường thẳng đi qua điểm gốc (0,0) có độ nghiêng bằng 1
Đồ thị của các hàm số cơ bản
Dạng hàm số Công thức Đồ thị
Hàm số đường thẳng
Hàm số đường thẳng qua 2 điểm bất kỳ
y
=
y
o
+
a
(
x
−
x
o
)
{\displaystyle y=y_{o}+a(x-x_{o})}
y
=
a
x
+
b
{\displaystyle y=ax+b}
x
o
=
0
,
y
o
=
b
{\displaystyle x_{o}=0,y_{o}=b}
Z
2
=
X
2
+
Y
2
{\displaystyle Z^{2}=X^{2}+Y^{2}}
Z
Z
2
=
X
Z
2
+
Y
Z
2
{\displaystyle {\frac {Z}{Z}}^{2}={\frac {X}{Z}}^{2}+{\frac {Y}{Z}}^{2}}
1
=
c
o
s
2
+
s
i
n
2
{\displaystyle 1=cos^{2}+sin^{2}}
1
=
s
e
c
2
+
t
a
n
2
{\displaystyle 1=sec^{2}+tan^{2}}
1
=
c
s
c
2
+
c
o
t
2
{\displaystyle 1=csc^{2}+cot^{2}}
y
=
a
x
n
{\displaystyle y=ax^{n}}
y
(
x
)
=
L
o
g
x
{\displaystyle y(x)=Logx}
c
o
s
θ
=
X
Z
{\displaystyle cos\theta ={\frac {X}{Z}}}
c
o
s
θ
=
Y
Z
{\displaystyle cos\theta ={\frac {Y}{Z}}}
c
o
s
θ
=
1
X
{\displaystyle cos\theta ={\frac {1}{X}}}
c
o
s
θ
=
1
Y
{\displaystyle cos\theta ={\frac {1}{Y}}}
c
o
s
θ
=
Y
X
{\displaystyle cos\theta ={\frac {Y}{X}}}
c
o
s
θ
=
X
Y
{\displaystyle cos\theta ={\frac {X}{Y}}}
Radial lines (those running through the pole) are represented by the equation
φ
=
γ
,
{\displaystyle \varphi =\gamma ,}
γ
{\displaystyle \gamma }
φ
=
arctan
m
{\displaystyle \varphi =\arctan m}
m
{\displaystyle m}
slope of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line
φ
=
γ
{\displaystyle \varphi =\gamma }
perpendicularly at the point
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
r
(
φ
)
=
r
0
sec
(
φ
−
γ
)
.
{\displaystyle r(\varphi )=r_{0}\sec(\varphi -\gamma ).}
Otherwise stated
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
r
0
{\displaystyle r_{0}}
A circle with equation r (φ ) = 1 The general equation for a circle with a center at
(
r
0
,
γ
)
{\displaystyle (r_{0},\gamma )}
a is
r
2
−
2
r
r
0
cos
(
φ
−
γ
)
+
r
0
2
=
a
2
.
{\displaystyle r^{2}-2rr_{0}\cos(\varphi -\gamma )+r_{0}^{2}=a^{2}.}
This can be simplified in various ways, to conform to more specific cases, such as the equation
r
(
φ
)
=
a
{\displaystyle r(\varphi )=a}
a .
When r 0 = a
r
=
2
a
cos
(
φ
−
γ
)
.
{\displaystyle r=2a\cos(\varphi -\gamma ).}
In the general case, the equation can be solved for r
r
=
r
0
cos
(
φ
−
γ
)
+
a
2
−
r
0
2
sin
2
(
φ
−
γ
)
{\displaystyle r=r_{0}\cos(\varphi -\gamma )+{\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\varphi -\gamma )}}}
A polar rose with equation r (φ ) = 2 sin 4φ A polar rose is a mathematical curve that looks like a petaled flower, and that can be expressed as a simple polar equation,
r
(
φ
)
=
a
cos
(
k
φ
+
γ
0
)
{\displaystyle r(\varphi )=a\cos \left(k\varphi +\gamma _{0}\right)}
for any constant γ0 (including 0). If k is an integer, these equations will produce a k -petaled rose if k is odd , or a 2k -petaled rose if k is even. If k is rational, but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable a directly represents the length or amplitude of the petals of the rose, while k relates to their spatial frequency. The constant γ0 can be regarded as a phase angle.
One arm of an Archimedean spiral with equation r (φ ) = φ / 2π 0 < φ < 6π pi The Archimedean spiral is a spiral discovered by Archimedes which can also be expressed as a simple polar equation. It is represented by the equation
r
(
φ
)
=
a
+
b
φ
.
{\displaystyle r(\varphi )=a+b\varphi .}
a will turn the spiral, while b controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for φ > 0φ < 0a = 0conic sections , to be described in a mathematical treatise, and as a prime example of a curve best defined by a polar equation.
Ellipse, showing semi-latus rectum A conic section with one focus on the pole and the other somewhere on the 0° ray (so that the conic's major axis lies along the polar axis) is given by:
r
=
ℓ
1
−
e
cos
φ
{\displaystyle r={\ell \over {1-e\cos \varphi }}}
e is the eccentricity and
ℓ
{\displaystyle \ell }
semi-latus rectum (the perpendicular distance at a focus from the major axis to the curve). If e > 1hyperbola ; if e = 1parabola ; and if e < 1ellipse . The special case e = 0
ℓ
{\displaystyle \ell }
Intersection of two polar curves [ sửa ] The graphs of two polar functions
r
=
f
(
θ
)
{\displaystyle r=f(\theta )}
r
=
g
(
θ
)
{\displaystyle r=g(\theta )}
In the origin, if the equations
f
(
θ
)
=
0
{\displaystyle f(\theta )=0}
g
(
θ
)
=
0
{\displaystyle g(\theta )=0}
All the points
[
g
(
θ
i
)
,
θ
i
]
{\displaystyle [g(\theta _{i}),\theta _{i}]}
θ
i
{\displaystyle \theta _{i}}
f
(
θ
+
2
k
π
)
=
g
(
θ
)
{\displaystyle f(\theta +2k\pi )=g(\theta )}
k
{\displaystyle k}
All the points
[
g
(
θ
i
)
,
θ
i
]
{\displaystyle [g(\theta _{i}),\theta _{i}]}
θ
i
{\displaystyle \theta _{i}}
f
(
θ
+
(
2
k
+
1
)
π
)
=
−
g
(
θ
)
{\displaystyle f(\theta +(2k+1)\pi )=-g(\theta )}
k
{\displaystyle k}
Thay đổi biến số x
Δ
x
=
(
x
+
Δ
x
)
−
x
{\displaystyle \Delta x=(x+\Delta x)-x}
Thay đổi biến số y
Δ
y
=
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=\Delta f(x)=f(x+\Delta x)-f(x)}
Biến đổi hàm số tính bằng tỉ lệ thay đổi biến số y trên thay đổi biến số x
Δ
y
Δ
x
=
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
(
x
+
Δ
x
)
−
x
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}}
d
d
x
f
(
x
)
=
f
′
(
x
)
=
lim
Δ
x
→
0
∑
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
∑
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=f^{'}(x)=\lim _{\Delta x\to 0}\sum {\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}\sum {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
Tích phân xác định
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)}
Tích phân bất định
∫
f
(
x
)
d
x
=
lim
Δ
x
→
0
∑
(
f
(
x
)
+
Δ
f
(
x
)
2
)
Δ
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)dx=\lim _{\Delta x\rightarrow 0}\sum (f(x)+{\frac {\Delta f(x)}{2}})\Delta x=F(x)+C}
Phương trình là một đẳng thức của một hàm số toán của 1 hay nhiều hơn một biến số có giá trị bằng không
f
(
x
)
=
0
{\displaystyle f(x)=0}
Với
x - Nghiệm số , mọi giá trị của x thỏa mản phương trình
f
(
x
)
=
0
{\displaystyle f(x)=0}
2
x
+
5
=
0
{\displaystyle 2x+5=0}
2
x
y
+
5
=
z
{\displaystyle 2xy+5=z}
x
2
+
4
x
−
12
=
0
{\displaystyle x^{2}+4x-12=0}
Giải phương trình là cách thức tìm giá trị của biến số sao cho hàm số của biến số có giá trị bằng không . Giá trị của biến số thỏa mản điều kiện f(x)=0 được gọi là nghiệm số của phương trình
2
x
+
4
=
6
{\displaystyle 2x+4=6}
2
x
=
6
−
4
=
2
{\displaystyle 2x=6-4=2}
x
=
2
/
2
=
1
{\displaystyle x=2/2=1}
[ sửa ] Dạng tổng quát
a
x
+
b
=
0
{\displaystyle ax+b=0}
Giải phương trình
a
x
+
b
=
0
{\displaystyle ax+b=0}
x
+
b
a
=
0
{\displaystyle x+{\frac {b}{a}}=0}
Nghiệm số phương trình
x
=
−
b
a
{\displaystyle x=-{\frac {b}{a}}}
[ sửa ] [ sửa ] Dạng tổng quát
X
2
+
Y
2
=
0
{\displaystyle X^{2}+Y^{2}=0}
Giải phương trình
X
=
−
Y
2
=
±
j
Y
{\displaystyle X={\sqrt {-Y^{2}}}=\pm jY}
Y
=
−
X
2
=
±
j
X
{\displaystyle Y={\sqrt {-X^{2}}}=\pm jX}
[ sửa ] Dạng tổng quát
X
+
j
Y
=
0
{\displaystyle X+jY=0}
Giải phương trình
X
=
−
j
Y
{\displaystyle X=-jY}
j
Y
=
−
X
{\displaystyle jY=-X}
Y
=
j
X
{\displaystyle Y=jX}
[ sửa ] [ sửa ] 





































































































![{\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83064172516d2185efbd65172ed7cc9d3e701284)
![{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ddb7d13541806e35a6053ba614df98a87b655)
![{\displaystyle {\sqrt[{n}]{ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbdd8f05f4d794abf4cccf685bf65c5f5776b98b)
![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)
![{\displaystyle {\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a67075d2bf5949cd4927199b5ad24ee5d609b0)






















































![{\displaystyle [e^{j\theta }]^{n}=e^{jn\theta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e251745b13431190d80c666a245aacb8cb406db7)




























![{\displaystyle a+(a+d)+(a+2d)+...+[a+(n-1)d]=\sum _{k=0}^{\infty }[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c5b6f1d86ff3f156fd65ff5857f5e95f89c10e)
![{\displaystyle \sum _{k=0}^{\infty }[a+(n-1)d]=a+(a+d)+(a+2d)+...+[a+(n-1)d]={\frac {n}{2}}(2a+(n-1)d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2a5db1feeaf9814ba2e7c2618c255f45f299a8)
![{\displaystyle S=a+(a+d)+(a+2d)+...+[a+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63777c0be192f9fe36871fbf7d21970aaed89899)
![{\displaystyle S=[a+(n-1)d]+...+(n-1)d]+a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c376b47de6ed1cfc662cad50bbc979688886f30)
![{\displaystyle 2S=[2a+(n-1)d]n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f47f5f57718103fa0610bc7149959105b3a09039)
![{\displaystyle S=[2a+(n-1)d]{\frac {n}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/220eac7734e9963f251e2cac7519edcaf6af5420)




















































![{\displaystyle A-B=(2x+5y-3)-(52y-5)=2x+(5y-52y)+[-3-(-5)]=2x-47y+2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b408c9cc2f522c6b7708d057b56b8972389ed9)















































































































![{\displaystyle [g(\theta _{i}),\theta _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3942e962cea54fd104a33ebac17dde8bffa819)

































































