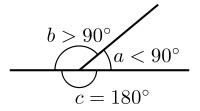Sách kỹ sư/Sách công thức toán
Công thức toán đại số
[sửa]Số đại số
[sửa]Loai số loại số Ký hiệu Thí dụ Số tự nhiên Số chẳn Số lẻ Số nguyên tố Số lũy thừa Số căn Số log Số nguyên Phân số Số thập phân Số hửu tỉ Số vô tỉ Số phức Số thực Số ảo Hằng số
Phép toán số đại số
[sửa]Toán Ký Hiệu Công Thức Định Nghỉa Toán cộng Toán Cộng hai số đại số Toán trừ Toán Trừ hai số đại số Toán nhân Toán Nhân hai số đại số Toán chia Toán Chia hai số đại số Toán lũy thừa Toán tìm tích n lần của chính số nhân Toán căn nếu có Toán lủy thừa nghịch Toán log Nếu có Toán Toán lủy thừa nghịch của một lủy thừa
Toán bội số
[sửa]Toán số nguyên
[sửa]Số 0
[sửa]Toán cộng Toán trừ Toán nhân toán chia
Số nguyên dương
[sửa]Toán cộng
Toán trừ
Toán nhân
Toán chia
Toán lũy thừa
Toán căn
=
Toán Log
for any
Số nguyên âm
[sửa]
Toán cộng
Toán cộng
Toán nhân
Toán chia
Toán lũy thừa
Vói
Với
Toán căn
Toán phân số
[sửa]
Phép toán chia hết
Khi chia a cho b cho thương số c và số dư r
a chia hết cho b khi . Vậy
a không chia hết cho b khi . Vậy
So sánh phân số
Với hai phân số và
Hai phân số bằng nhau khi
Hay
Hai phân số không bằng nhau khi
Toán cộng , trừ, nhân, chia
Toán lũy thừa
[sửa]Lủy thừa không Lủy thừa 1 Lủy thừa của số không Lủy thừa của số 1 Lủy thừa trừ Lủy thừa phân số Lủy thừa của số nguyên âm
Với .
. VớiLủy thừa của số nguyên dương Lủy thừa của lủy thừa Lủy thừa của tích hai số Lủy thừa của thương hai số Lủy thừa của căn Cộng trừ nhân chia 2 lủy thừa
Lủy thừa của tổng hai số
Lủy thừa của hiệu hai số
Hiệu 2 lũy thừa Tổng 2 lũy thừa
Toán căn
[sửa]Căn và lủy thừa Căn của số nguyên
Căn lủy thừa
Căn thương số
Căn tích số
=Vô căn
Ra căn
Toán log
[sửa]Toán Log khi có Viết tắc
Log 1
Log lũy thừa
Lũy thừa log
Log của tích số
Log của thương số
Log của lủy thừa
Đổi nền log
Toán số ảo
[sửa]Cộng trừ nhân chia 2 số ảo
Lủy thừa số ảo nguyên dương
Từ trên, ta có
với
vớiLủy thừa số ảo nguyên âm
Từ trên, ta có
với
với
Toán số phức
[sửa]Với 2 số phức thuận nghịch
Số phức thuận Số phức nghịch
+ - x / Định luật De Moive
Toán hàm số
[sửa]Đồ thị
[sửa]Hàm số đường thẳng

Hàm số đường tròn Hàm số đường cong lùy thừa 
Hàm số đường cong căn Hàm số đường cong log 
Hàm số lượng giác Cos 
Hàm số lượng giác Sin 
Hàm số lượng giác Tan 
Hàm số lượng giác Cotan 
Hàm số lượng giác Sec 
Hàm số lượng giác Cosec 
Giải tích
[sửa]Phép toán Công thức Thay đổi biến số
Biến đổi hàm số
Giới hạn
Tổng số
Đạo hàm
Tích phân
Tích phân xác định
Tích phân bất định
Biểu diển hàm số bằng tổng dải số
[sửa]Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
- Chứng minh
Khi x=0
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
Thế vào hàm số ở trên ta được
- Thí dụ
Phương trình
[sửa]Giải phương trình lũy thừa
[sửa]Phương trình lũy thừa Dạng tổng quát Giải phương trình Phương trình lũy thừa bậc 1

Giải phương trình lũy thừa bậc 2
:
.
.
.
v
Giải phương trình lũy thừa bậc n
Giải phương trình đạo hàm
[sửa]Phương trình đạo hàm Dạng tổng quát Giải phương trình Phương trình đạo hàm bậc n Phương trình đạo hàm bậc 2
. . =
. . <
. . >
. . .Phương trình đạo hàm bậc 1
Giải hệ phương trình tuyến tính
[sửa]Công thức toán hình học
[sửa]Hình Tam giác thường
[sửa]Định lý Sin
[sửa]Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng
- .
trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:
Định lý Cosin
[sửa]Hình Tam giác đều
[sửa]Hình Tam giác có 3 cạnh và 3 góc bằng nhau
- AB = BC = CA
Hình Tam giác cân
[sửa]Hình Tam giác vuông
[sửa]Định lý Pytago
[sửa]Định lý Pytago phát biểu rằng:
- Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này . Nó được thể hiện bằng phương trình
Trong đó, c là chiều dài của cạnh huyền và a và b là chiều dài của hai cạnh còn lại.
Hàm số góc lượng giác
[sửa]Tương quan các cạnh và góc
Tam giác vuông trên đồ thị XY
[sửa]Hàm số cạnh Độ dài cạnh ngang
Độ dài cạnh dọc Độ dóc Độ nghiêng
Vector đương thẳng ngang
Vector đương thẳng dọc Vector đương thẳng nghiêng
Hàm số Đường thẳng nghiêng ở độ dóc Z
Hàm số Đường thẳng nghiêng ở độ góc nghiêng θ
Diện tích dưới hình
Hình Tam giác vuông cân
[sửa]Hình vuông
[sửa]Hình chữ nhựt
[sửa]Hình bình hành
[sửa]Hình thoi
[sửa]Hình thang
[sửa]Hình tròn
[sửa]Hình nón
[sửa]Hình cong
[sửa]Công thức toán lượng giác
[sửa]Điểm
[sửa]Góc Định nghỉa Ký hiệu Đơn vị Thí dụ . Một chấm A __ B
Đường thẳng
[sửa]Góc
[sửa]Góc Định nghỉa Ký hiệu Đơn vị Thí dụ 
Khi hai đường thẳng cắt nhau tại một điểm
sẽ tạo ra một góc giữa hai đường thẳng
Hàm số lượng giác
[sửa]Phương trình lượng giác
[sửa]Công thức toán giải tích
[sửa]Phép toán Công thức Thay đổi biến số
Biến đổi hàm số
Giới hạn
Tổng số
Đạo hàm
Tích phân
Tích phân xác định
Tích phân bất định












































































![{\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}=a^{\frac {1}{mn}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83064172516d2185efbd65172ed7cc9d3e701284)
![{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ddb7d13541806e35a6053ba614df98a87b655)
![{\displaystyle {\sqrt[{n}]{ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbdd8f05f4d794abf4cccf685bf65c5f5776b98b)
![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)
![{\displaystyle {\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a67075d2bf5949cd4927199b5ad24ee5d609b0)
































































































































![{\displaystyle [e^{j\theta }]^{n}=e^{jn\theta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e251745b13431190d80c666a245aacb8cb406db7)