Có 2 loại điện thông dụng bao gồm Điện DC và Điện AC . Điện DC thông thường được tìm thấy ở Pin, Ắc quy, Pin mặt trời có Điện thế khoảng 1.5 V đến 12 V được tạo ra từ nhiều nguồn phát điện như Điện giải , Điện cực , Quang tuyến nhiệt điện và Biến điện AC ra điện DC . Điện AC được tạo ra từ máy phát điện AC có Điện thế 120V - 60 Hz
Được tìm thấy ở Pin , Ắc quy , Pin mặt trời có Điện thế khoảng 1.5 V đến 12 V được tạo ra từ nhiều nguồn phát điện như
.
Điện DC có điện thế không đổi theo thời gian
Ký hiệu
Công thức toán sau
v
(
t
)
=
V
{\displaystyle v(t)=V}
Dòng điện
I
=
Q
t
{\displaystyle I={\frac {Q}{t}}}
Điện lượng
Q
=
I
t
{\displaystyle Q=It}
Điện thế
V
=
W
Q
{\displaystyle V={\frac {W}{Q}}}
Năng lực
W
=
Q
V
{\displaystyle W=QV}
Năng lượng
P
=
W
t
=
Q
V
t
=
I
V
{\displaystyle P={\frac {W}{t}}={\frac {QV}{t}}=IV}
Điện AC được tạo ra từ máy phát điện AC có Điện thế 120V - 60 Hz
Điện AC hay Điện hai chiều có điện thế thay đổi theo thời gian của một sóng sin đều
Ký hiệu
Công thức toán
v
(
t
)
=
V
sin
ω
t
{\displaystyle v(t)=V\sin \omega t}
Dòng điện
i
(
t
)
=
d
d
t
Q
(
t
)
{\displaystyle i(t)={\frac {d}{dt}}Q(t)}
Điện lượng
Q
(
t
)
=
∫
i
(
t
)
d
t
{\displaystyle Q(t)=\int i(t)dt}
Điện thế
v
(
t
)
=
d
d
t
W
(
t
)
Q
(
t
)
{\displaystyle v(t)={\frac {d}{dt}}{\frac {W(t)}{Q(t)}}}
Năng lực
W
(
t
)
=
∫
v
(
t
)
[
Q
(
t
)
d
t
]
d
t
=
∫
v
(
t
)
i
(
t
)
d
t
{\displaystyle W(t)=\int v(t)[Q(t)dt]dt=\int v(t)i(t)dt}
Năng lượng
U
(
t
)
=
d
d
t
W
(
t
)
=
d
d
t
∫
v
(
t
)
i
(
t
)
d
t
{\displaystyle U(t)={\frac {d}{dt}}W(t)={\frac {d}{dt}}\int v(t)i(t)dt}
[ sửa ] Điện trở kháng
R
=
V
I
{\displaystyle R={\frac {V}{I}}}
Điện thế
V
=
I
R
{\displaystyle V=IR}
Dòng điện
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
Điện năng
P
=
I
V
=
I
2
R
=
V
2
R
{\displaystyle P=IV=I^{2}R={\frac {V^{2}}{R}}}
Điện ứng
X
=
v
(
t
)
i
(
t
{\displaystyle X={\frac {v(t)}{i(t}}}
Điện kháng
Z
=
R
+
X
{\displaystyle Z=R+X}
Điện trở kháng của điện trở được tính theo Định luật Ohm
R
=
V
I
{\displaystyle R={\frac {V}{I}}}
G
=
I
V
=
1
R
{\displaystyle G={\frac {I}{V}}={\frac {1}{R}}}
Điện thế của điện trở được tính theo Định luật Volt
V
=
I
R
{\displaystyle V=IR}
Dòng điện của điện trở được tính theo Định luật Ampere
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
i
(
t
)
=
v
(
t
)
X
{\displaystyle i(t)={\frac {v(t)}{X}}}
v
(
t
)
=
i
(
t
)
X
{\displaystyle v(t)=i(t)X}
p
(
t
)
=
v
(
t
)
i
(
t
)
{\displaystyle p(t)=v(t)i(t)}
X
R
=
v
(
t
)
i
(
t
)
=
0
{\displaystyle X_{R}={\frac {v(t)}{i(t)}}=0}
Z
R
=
R
+
X
R
=
R
∠
0
=
R
=
r
{\displaystyle Z_{R}=R+X_{R}=R\angle 0=R=r}
Từ cảm của cuộn từ
B
=
L
I
{\displaystyle B=LI}
Dòng điện trong cuộn từ
I
=
B
L
{\displaystyle I={\frac {B}{L}}}
Từ dung của cuộn từ
L
=
B
I
{\displaystyle L={\frac {B}{I}}}
v
(
t
)
=
L
d
d
t
i
(
t
)
{\displaystyle v(t)=L{\frac {d}{dt}}i(t)}
i
(
t
)
=
1
L
∫
i
(
v
)
d
t
{\displaystyle i(t)={\frac {1}{L}}\int i(v)dt}
p
(
t
)
=
∫
B
d
i
=
∫
L
i
d
i
=
1
2
L
i
2
{\displaystyle p(t)=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}}
X
L
=
v
(
t
)
i
(
t
)
=
ω
L
∠
90
=
j
ω
L
=
s
L
{\displaystyle X_{L}={\frac {v(t)}{i(t)}}=\omega L\angle 90=j\omega L=sL}
Z
L
=
R
+
X
L
=
R
∠
0
+
ω
L
∠
90
=
R
+
j
ω
L
=
R
+
s
L
{\displaystyle Z_{L}=R+X_{L}=R\angle 0+\omega L\angle 90=R+j\omega L=R+sL}
Điện lượng của Tụ điện
Q
=
C
V
{\displaystyle Q=CV}
Điện thế của Tụ điện
V
=
Q
C
{\displaystyle V={\frac {Q}{C}}}
Điện dung của Tụ điện
C
=
Q
V
{\displaystyle C={\frac {Q}{V}}}
i
(
t
)
=
C
d
d
t
v
(
t
)
{\displaystyle i(t)=C{\frac {d}{dt}}v(t)}
v
(
t
)
=
1
C
∫
i
(
t
)
d
t
{\displaystyle v(t)={\frac {1}{C}}\int i(t)dt}
p
(
t
)
=
∫
Q
d
v
=
∫
C
v
d
t
=
1
2
C
v
2
{\displaystyle p(t)=\int Qdv=\int Cvdt={\frac {1}{2}}Cv^{2}}
X
R
=
v
(
t
)
i
(
t
)
=
1
ω
C
∠
−
90
=
1
j
ω
C
=
1
s
C
{\displaystyle X_{R}={\frac {v(t)}{i(t)}}={\frac {1}{\omega C}}\angle -90={\frac {1}{j\omega C}}={\frac {1}{sC}}}
Z
R
=
R
+
X
C
=
R
∠
0
+
1
ω
C
∠
−
90
=
R
+
1
j
ω
C
=
R
+
1
s
C
{\displaystyle Z_{R}=R+X_{C}=R\angle 0+{\frac {1}{\omega C}}\angle -90=R+{\frac {1}{j\omega C}}=R+{\frac {1}{sC}}}
Mạch điện điện tử là một vòng khép kín của nhiều linh kiện điện tử mắc nối với nhau theo một lối mắc nhứt định để tạo thành các Bộ phận điện tử có khả năng thực thi một việc
Định luật Kirchhoff được dùng để mô tả mối quan hệ của cường độ dòng điện và điện áp trong mạch điện . Các định luật này được Gustav Kirchhoff xây dựng vào năm 1845 bao gồm 2 định luật sau
[ sửa ] Tổng giá trị đại số của dòng điện tại một nút trong một mạch điện là bằng không . Tại bất kỳ nút (ngã rẽ) nào trong một mạch điện, thì tổng cường độ dòng điện chạy đến nút phải bằng tổng cường độ dòng điện từ nút chạy đi
∑
k
=
1
n
I
k
=
0
{\displaystyle \sum _{k=1}^{n}{I}_{k}=0}
n là tổng số các nhánh với dòng điện chạy vào nút hay từ nút ra.
∑
k
=
1
n
I
~
k
=
0
{\displaystyle \sum _{k=1}^{n}{\tilde {I}}_{k}=0}
[ sửa ] Tổng giá trị điện áp dọc theo một vòng bằng không
∑
k
=
1
n
V
k
=
0
{\displaystyle \sum _{k=1}^{n}V_{k}=0}
n là tổng số các điện áp được đo.
∑
k
=
1
n
V
~
k
=
0
{\displaystyle \sum _{k=1}^{n}{\tilde {V}}_{k}=0}
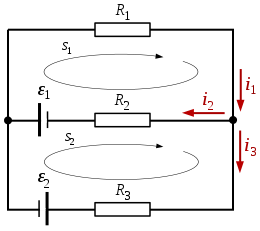
Thí dụ
Theo định luật 1, ta có:
i
1
−
i
2
−
i
3
=
0
{\displaystyle i_{1}-i_{2}-i_{3}=0\,}
Định luật 2 áp dụng cho vòng s 1 :
−
R
2
i
2
+
ϵ
1
−
R
1
i
1
=
0
{\displaystyle -R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}=0}
Định luật 2 áp dụng cho vòng s 2 :
−
R
3
i
3
−
ϵ
2
−
ϵ
1
+
R
2
i
2
=
0
{\displaystyle -R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}=0}
Đến đây ta có hệ phương trình tuyến tính cho 3 ẩn số
i
1
,
i
2
,
i
3
{\displaystyle i_{1},i_{2},i_{3}}
{
i
1
−
i
2
−
i
3
=
0
−
R
2
i
2
+
ϵ
1
−
R
1
i
1
=
0
−
R
3
i
3
−
ϵ
2
−
ϵ
1
+
R
2
i
2
=
0
{\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}&=0\\\end{cases}}}
Giả sử:
R
1
=
100
,
R
2
=
200
,
R
3
=
300
(ohm)
;
ϵ
1
=
3
,
ϵ
2
=
4
(volt)
{\displaystyle R_{1}=100,\ R_{2}=200,\ R_{3}=300{\text{ (ohm)}};\ \epsilon _{1}=3,\ \epsilon _{2}=4{\text{ (volt)}}}
kết quả:
{
i
1
=
1
1100
hay
0.
90
¯
mA
i
2
=
4
275
hay
14.
54
¯
mA
i
3
=
−
3
220
hay
−
13.
63
¯
mA
{\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{ hay }}0.{\bar {90}}{\text{ mA}}\\i_{2}={\frac {4}{275}}{\text{ hay }}14.{\bar {54}}{\text{ mA}}\\i_{3}=-{\frac {3}{220}}{\text{ hay }}-13.{\bar {63}}{\text{ mA}}\\\end{cases}}}
i
3
{\displaystyle i_{3}}
i
3
{\displaystyle i_{3}}
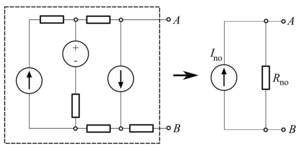
Mọi mạch điện đều có thể biểu diển bằng mạch điện tương đương của mạch điện song song của dòng điện nguồn và điên dần tổng sau
Mọi mạch điện đều có thể biểu diển bằng mạch điện nối tiếp của một điện thế và điện kháng như sau
Có 4 lối mắc mạch điện cơ bản sau nối tiếp, song song, 2 cổng và tích hợp
Có các linh kiện điện mắc nối kề nhau trong một vòng tròn khép kín
V
=
I
R
1
+
I
R
2
+
.
.
.
+
I
R
n
=
I
(
R
1
+
R
2
+
.
.
.
+
R
n
)
{\displaystyle V=IR_{1}+IR_{2}+...+IR_{n}=I(R_{1}+R_{2}+...+R_{n})}
R
t
=
V
I
=
(
R
1
+
R
2
+
.
.
.
+
R
n
)
{\displaystyle R_{t}={\frac {V}{I}}=(R_{1}+R_{2}+...+R_{n})}
I
=
V
R
t
=
V
R
1
+
R
2
+
.
.
.
+
R
n
{\displaystyle I={\frac {V}{R_{t}}}={\frac {V}{R_{1}+R_{2}+...+R_{n}}}}
Có các linh kiện điện mắc nối thẳng đứng đối diện nhau trong một vòng tròn khép kín
I
=
I
1
+
I
2
+
.
.
.
+
I
n
=
V
R
1
+
V
R
2
+
.
.
.
+
V
R
n
=
V
(
1
R
1
+
1
R
2
+
.
.
.
+
1
R
n
)
{\displaystyle I=I_{1}+I_{2}+...+I_{n}={\frac {V}{R_{1}}}+{\frac {V}{R_{2}}}+...+{\frac {V}{R_{n}}}=V({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+...+{\frac {1}{R_{n}}})}
I
V
=
1
R
1
+
1
R
2
+
.
.
.
+
1
R
n
=
1
R
t
=
G
t
{\displaystyle {\frac {I}{V}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+...+{\frac {1}{R_{n}}}={\frac {1}{R_{t}}}=G_{t}}
V
=
I
G
t
{\displaystyle V={\frac {I}{G_{t}}}}
Có các linh kiện điện tử mắc nối với nhau tạo ra 2 cổng nhập và xuất
V
o
=
I
R
2
=
V
i
R
1
+
R
2
R
2
{\displaystyle V_{o}=IR_{2}={\frac {V_{i}}{R_{1}+R_{2}}}R_{2}}
V
o
V
i
=
R
2
R
1
+
R
2
{\displaystyle {\frac {V_{o}}{V_{i}}}={\frac {R_{2}}{R_{1}+R_{2}}}}
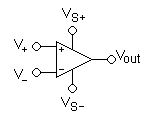
Chân của Op Amp
1 Chỉnh Không
Con chíp IC 741 có khả năng khuếch đại hiệu hai điện thế nhập
Khuếch đại hiệu hai điện thế
V
o
=
A
(
V
2
−
V
1
)
{\displaystyle V_{o}=A(V_{2}-V_{1})}
Khuếch đại điện âm
V
o
=
−
A
V
1
.
V
2
=
0
{\displaystyle V_{o}=-AV_{1}.V_{2}=0}
Khuếch đại điện dương
V
o
=
A
V
2
.
V
1
=
0
{\displaystyle V_{o}=AV_{2}.V_{1}=0}
So sánh điện thế
V
o
=
0.
V
2
=
V
1
{\displaystyle V_{o}=0.V_{2}=V_{1}}
V
o
=
V
+
.
V
2
>
V
1
{\displaystyle V_{o}=V_{+}.V_{2}>V_{1}}
V
o
=
V
−
.
V
2
<
V
1
{\displaystyle V_{o}=V_{-}.V_{2}<V_{1}}
[ sửa ] Mạch điện RLC nối tiếp . Mạch điện điện tử của 3 linh kiện điện tử R, L và C mắc nối tiếp với nhau
[ sửa ] Ỏ trạng thái cân bằng
V
L
+
V
C
+
V
R
=
0
{\displaystyle V_{L}+V_{C}+V_{R}=0}
L
d
2
i
d
t
2
+
1
C
∫
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {d^{2}i}{dt^{2}}}+{\frac {1}{C}}\int idt+iR=0}
d
2
i
d
t
2
+
R
L
d
i
d
t
+
1
L
C
i
=
0
{\displaystyle {\frac {d^{2}i}{dt^{2}}}+{\frac {R}{L}}{\frac {di}{dt}}+{\frac {1}{LC}}i=0}
s
2
i
+
R
L
s
i
+
1
L
C
i
=
0
{\displaystyle s^{2}i+{\frac {R}{L}}si+{\frac {1}{LC}}i=0}
s
2
+
2
α
s
+
β
=
0
{\displaystyle s^{2}+2\alpha s+\beta =0}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
λ
{\displaystyle \lambda }
ω
{\displaystyle \omega }
R
2
L
{\displaystyle {\frac {R}{2L}}}
1
L
C
{\displaystyle {\frac {1}{LC}}}
α
−
β
{\displaystyle {\sqrt {\alpha -\beta }}}
β
−
α
{\displaystyle {\sqrt {\beta -\alpha }}}
s
{\displaystyle s}
α
,
β
{\displaystyle \alpha ,\beta }
f
(
t
)
=
A
e
s
t
{\displaystyle f(t)=Ae^{st}}
α
{\displaystyle \alpha }
α
=
β
{\displaystyle \alpha =\beta }
i
=
A
e
−
α
t
=
A
(
α
)
{\displaystyle i=Ae^{-\alpha t}=A(\alpha )}
α
±
λ
{\displaystyle \alpha \pm \lambda }
α
>
β
{\displaystyle \alpha >\beta }
i
=
A
e
(
−
α
±
λ
)
t
=
A
(
α
)
e
λ
t
+
A
(
α
)
e
−
λ
t
{\displaystyle i=Ae^{(-\alpha \pm \lambda )t}=A(\alpha )e^{\lambda t}+A(\alpha )e^{-\lambda t}}
α
±
j
ω
{\displaystyle \alpha \pm j\omega }
α
>
β
{\displaystyle \alpha >\beta }
i
=
A
e
(
−
α
±
λ
)
t
=
A
(
α
)
s
i
n
ω
t
{\displaystyle i=Ae^{(-\alpha \pm \lambda )t}=A(\alpha )sin\omega t}
A
(
α
)
=
A
e
−
α
t
{\displaystyle A(\alpha )=Ae^{-\alpha t}}
Ở trạng thái đồng bộ
Z
t
=
Z
L
+
Z
C
+
Z
R
=
R
{\displaystyle Z_{t}=Z_{L}+Z_{C}+Z_{R}=R}
Z
C
+
Z
L
=
0
{\displaystyle Z_{C}+Z_{L}=0}
ω
L
=
−
1
ω
C
{\displaystyle \omega L=-{\frac {1}{\omega C}}}
ω
o
=
−
1
L
C
=
±
j
1
L
C
=
±
j
1
T
{\displaystyle \omega _{o}={\sqrt {-{\frac {1}{LC}}}}=\pm j{\sqrt {\frac {1}{LC}}}=\pm j{\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
i
(
ω
=
0
)
=
0
{\displaystyle i(\omega =0)=0}
i
(
ω
=
ω
o
)
=
v
R
{\displaystyle i(\omega =\omega _{o})={\frac {v}{R}}}
i
(
ω
=
00
)
=
0
{\displaystyle i(\omega =00)=0}
[ sửa ]
V
L
+
V
C
=
0
{\displaystyle V_{L}+V_{C}=0}
L
d
2
i
d
t
2
+
1
C
∫
i
d
t
=
0
{\displaystyle L{\frac {d^{2}i}{dt^{2}}}+{\frac {1}{C}}\int idt=0}
d
2
i
d
t
2
+
1
L
C
i
=
0
{\displaystyle {\frac {d^{2}i}{dt^{2}}}+{\frac {1}{LC}}i=0}
d
2
i
d
t
2
=
−
1
T
i
{\displaystyle {\frac {d^{2}i}{dt^{2}}}=-{\frac {1}{T}}i}
i
=
A
e
−
1
T
t
=
A
e
±
j
ω
t
=
A
sin
ω
t
{\displaystyle i=Ae^{{\sqrt {-{\frac {1}{T}}}}t}=Ae^{\pm j\omega t}=A\sin \omega t}
ω
=
1
T
{\displaystyle \omega ={\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
Z
C
=
−
Z
L
{\displaystyle Z_{C}=-Z_{L}}
V
C
=
−
V
L
{\displaystyle V_{C}=-V_{L}}
v
(
θ
)
=
A
sin
(
ω
o
t
+
2
π
)
−
A
sin
(
ω
o
t
−
2
π
)
{\displaystyle v(\theta )=A\sin(\omega _{o}t+2\pi )-A\sin(\omega _{o}t-2\pi )}
ω
o
=
±
j
1
T
{\displaystyle \omega _{o}=\pm j{\sqrt {\frac {1}{T}}}}
T
=
L
C
{\displaystyle T=LC}
[ sửa ] Ở trạng thái cân bằng
v
C
+
v
R
=
0
{\displaystyle v_{C}+v_{R}=0}
C
d
v
d
t
+
v
R
=
0
{\displaystyle C{\frac {dv}{dt}}+{\frac {v}{R}}=0}
d
v
d
t
=
−
1
T
{\displaystyle {\frac {dv}{dt}}=-{\frac {1}{T}}}
d
v
v
=
−
1
T
d
t
{\displaystyle {\frac {dv}{v}}=-{\frac {1}{T}}dt}
∫
d
v
v
=
−
1
T
∫
d
t
{\displaystyle \int {\frac {dv}{v}}=-{\frac {1}{T}}\int dt}
L
n
v
=
−
1
T
t
+
c
{\displaystyle Lnv=-{\frac {1}{T}}t+c}
v
=
e
−
1
T
t
+
c
=
A
e
−
1
T
t
{\displaystyle v=e^{-{\frac {1}{T}}t+c}=Ae^{-{\frac {1}{T}}t}}
T
=
R
C
{\displaystyle T=RC}
[ sửa ] Ở trạng thái cân bằng
v
L
+
v
R
=
0
{\displaystyle v_{L}+v_{R}=0}
L
d
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {di}{dt}}+iR=0}
d
i
d
t
=
−
1
T
{\displaystyle {\frac {di}{dt}}=-{\frac {1}{T}}}
d
i
i
=
−
1
T
d
t
{\displaystyle {\frac {di}{i}}=-{\frac {1}{T}}dt}
∫
d
i
v
=
−
1
T
∫
d
t
{\displaystyle \int {\frac {di}{v}}=-{\frac {1}{T}}\int dt}
L
n
i
=
−
1
T
t
+
c
{\displaystyle Lni=-{\frac {1}{T}}t+c}
i
=
e
−
1
T
t
+
c
=
A
e
−
1
T
t
{\displaystyle i=e^{-{\frac {1}{T}}t+c}=Ae^{-{\frac {1}{T}}t}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
[ sửa ]
∇
2
E
=
−
ω
E
{\displaystyle \nabla ^{2}E=-\omega E}
∇
2
B
=
−
ω
B
{\displaystyle \nabla ^{2}B=-\omega B}
E
=
A
sin
ω
t
{\displaystyle E=A\sin \omega t}
B
=
A
sin
ω
t
{\displaystyle B=A\sin \omega t}
ω
=
1
T
{\displaystyle \omega ={\sqrt {\frac {1}{T}}}}
T
=
μ
ϵ
{\displaystyle T=\mu \epsilon }
∇
2
E
=
−
ω
o
E
{\displaystyle \nabla ^{2}E=-\omega _{o}E}
∇
2
B
=
−
ω
o
B
{\displaystyle \nabla ^{2}B=-\omega _{o}B}
E
=
A
sin
ω
o
t
{\displaystyle E=A\sin \omega _{o}t}
B
=
A
sin
ω
o
t
{\displaystyle B=A\sin \omega _{o}t}
ω
o
=
1
T
o
{\displaystyle \omega _{o}={\sqrt {\frac {1}{T_{o}}}}}
T
o
=
μ
o
ϵ
o
{\displaystyle T_{o}=\mu _{o}\epsilon _{o}}
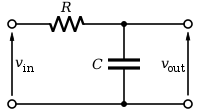
Mạch điện của các linh kiện điện tử mắc nối với nhau cho một điện ổn ở một dải tần số thời gian . Bộ lọc là một bộ phận điện tử tạo từ nhiều linh kiện điện tử mắc nối với nhau cho điện ổn ở một dải tần số
Bộ lọc điện tử Lối mắc Tính chất
Bộ lọc tần số thấp
v
o
v
2
=
1
j
ω
C
R
+
1
j
ω
C
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {\frac {1}{j\omega C}}{R+{\frac {1}{j\omega C}}}}={\frac {1}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
=
1
R
C
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {1}{RC}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
v
o
v
2
=
R
R
=
j
ω
L
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {R}{R=j\omega L}}={\frac {1}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
Bộ lọc điện tử Lối mắc Tính chất
Bộ lọc tần số cao
v
o
v
2
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {j\omega T}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
=
1
R
C
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {1}{RC}}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
v
o
v
2
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {j\omega T}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ lọc điện tử Lối mắc Tính chất
Bộ lọc băng tần
v
o
v
i
=
(
1
1
+
j
ω
T
L
)
(
j
ω
T
H
1
+
j
ω
H
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=({\frac {1}{1+j\omega T_{L}}})({\frac {j\omega T_{H}}{1+j\omega _{H}}})}
T
L
=
L
R
{\displaystyle T_{L}={\frac {L}{R}}}
T
H
=
R
C
{\displaystyle T_{H}=RC}
ω
L
−
ω
H
=
R
L
−
1
R
C
{\displaystyle \omega _{L}-\omega _{H}={\frac {R}{L}}-{\frac {1}{RC}}}
v
o
v
i
=
(
1
1
+
j
ω
T
L
)
(
j
ω
T
H
1
+
j
ω
H
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=({\frac {1}{1+j\omega T_{L}}})({\frac {j\omega T_{H}}{1+j\omega _{H}}})}
T
L
=
R
C
{\displaystyle T_{L}=RC}
T
H
=
L
R
{\displaystyle T_{H}={\frac {L}{R}}}
ω
L
−
ω
H
=
1
R
C
−
R
L
{\displaystyle \omega _{L}-\omega _{H}={\frac {1}{RC}}-{\frac {R}{L}}}
[ sửa ]
Bộ lọc điện tử Lối mắc Tính chất
Bộ lọc băng tần chọn lựa
v
o
v
i
=
R
R
+
j
ω
L
+
1
j
ω
C
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega L+{\frac {1}{j\omega C}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
{\displaystyle v_{o}(\omega =\omega _{o})=v_{i}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
v
o
v
i
=
j
ω
C
+
1
j
ω
L
R
+
j
ω
C
+
1
j
ω
L
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega C+{\frac {1}{j\omega L}}}{R+j\omega C+{\frac {1}{j\omega L}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
{\displaystyle v_{o}(\omega =\omega _{o})=v_{i}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
Mạch điện bộ lọc băng tần chọn lược
Bộ lọc điện tử Lối mắc Tính chất
Bộ lọc băng tần chọn lược
v
o
v
i
=
R
R
+
j
ω
L
+
1
j
ω
C
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega L+{\frac {1}{j\omega C}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
0
{\displaystyle v_{o}(\omega =\omega _{o})=0}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
v
o
v
i
=
j
ω
C
+
1
j
ω
L
R
+
j
ω
C
+
1
j
ω
L
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega C+{\frac {1}{j\omega L}}}{R+j\omega C+{\frac {1}{j\omega L}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
0
{\displaystyle v_{o}(\omega =\omega _{o})=0}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ ổn điện là một bộ phận điện tử cung cấp một điện thế ổn không đổi
Lối mắc mạch điện 2 cổng của một Điện trở và một Diot zener . Lối mắc này cho một điện thế ổn định ở cổng xuất bằng với điện thế
v
Z
{\displaystyle v_{Z}}
Bộ khuếch đại điện âm
v
o
=
−
A
v
i
{\displaystyle v_{o}=-Av_{i}}
Bộ khuếch đại điện dương
v
o
=
A
v
i
{\displaystyle v_{o}=Av_{i}}
Bộ khuếch đại điện âm
v
o
=
[
1
−
R
2
R
2
+
R
1
R
4
R
3
]
v
i
{\displaystyle v_{o}=[1-{\frac {R_{2}}{R_{2}+R_{1}}}{\frac {R_{4}}{R_{3}}}]v_{i}}
v
o
=
−
n
v
i
{\displaystyle v_{o}=-nv_{i}}
R
1
=
0
,
R
4
=
(
n
+
1
)
R
3
{\displaystyle R_{1}=0,R_{4}=(n+1)R_{3}}
Bộ khuếch đại điện dương
v
o
=
[
R
2
R
2
+
R
1
R
4
R
3
]
v
i
{\displaystyle v_{o}=[{\frac {R_{2}}{R_{2}+R_{1}}}{\frac {R_{4}}{R_{3}}}]v_{i}}
v
o
=
n
v
i
{\displaystyle v_{o}=nv_{i}}
R
1
=
0
,
R
4
=
n
R
3
{\displaystyle R_{1}=0,R_{4}=nR_{3}}
Bộ khuếch đại điện âm
v
o
=
−
R
2
R
1
v
i
{\displaystyle v_{o}=-{\frac {R_{2}}{R_{1}}}v_{i}}
v
o
=
−
n
v
i
{\displaystyle v_{o}=-nv_{i}}
R
2
=
n
R
1
{\displaystyle R_{2}=nR_{1}}
Bộ khuếch đại điện dương
v
o
=
[
1
+
R
2
R
1
]
v
i
{\displaystyle v_{o}=[1+{\frac {R_{2}}{R_{1}}}]v_{i}}
v
o
=
n
v
i
{\displaystyle v_{o}=nv_{i}}
R
2
=
n
R
1
{\displaystyle R_{2}=nR_{1}}
R
2
R
1
>>
1
{\displaystyle {\frac {R_{2}}{R_{1}}}>>1}
Lối mắc cơ bản
Micro ------ Loa Lối mắc khác
Micro ------ Khuếch đại ------ Loa 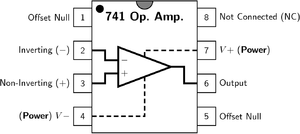



















![{\displaystyle W(t)=\int v(t)[Q(t)dt]dt=\int v(t)i(t)dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee6ba617fbc92542f6af349194b9acd77ea433a3)




































































































































































![{\displaystyle v_{o}=[1-{\frac {R_{2}}{R_{2}+R_{1}}}{\frac {R_{4}}{R_{3}}}]v_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f23c6cc1a1812b6b55ba04cd11d72a0ad4e925a)


![{\displaystyle v_{o}=[{\frac {R_{2}}{R_{2}+R_{1}}}{\frac {R_{4}}{R_{3}}}]v_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a333eef978b20078104b80c59789c7e16e7a3a77)




![{\displaystyle v_{o}=[1+{\frac {R_{2}}{R_{1}}}]v_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f93e6adc59d47eef36061c9d161756de3bee7588)
