Sách hình học/Hình tam giác/Tam giác đều

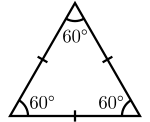
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau, và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.

Tam giác có 3 cạnh và 3 góc bằng nhau .

3 cạnh bằng nhau . $AB=BC=CA$
3 cạnh góc nhau . $\angle A=\angle B=\angle C={\frac {180^{o}}{3}}=60^{o}$

Tam giác có 3 cạnh bằng nhau là tam giác đều
Tam giác có 3 góc bằng nhau là tam giác đều
Tam giác cân có một góc bằng 60° là tam giác đều
Tam giác có 2 góc bằng 60 độ là tam giác đều

Chu vi Diện tích Thể tích

Chu vi	$AB+BC+CA=3C$
Diện tích	${\frac {C}{2}}\times h$
Thể tích	$AB\times BC\times CA=C^{3}$

Tính chất

Giả sử độ dài ba cạnh tam giác đều bằng $a\,\!$ , dùng định lý Pytago chứng minh được:

Diện tích: $A=a^{2}{\frac {\sqrt {3}}{4}}$
Chu vi: $p=3a\,\!$
Bán kính đường tròn ngoại tiếp $R=a{\frac {\sqrt {3}}{3}}$
Bán kính đường tròn nội tiếp $r=a{\frac {\sqrt {3}}{6}}$
Trọng tâm của tam giác cũng là tâm của đường tròn nội tiếp và ngoại tiếp
Chiều cao của tam giác đều $h=a{\frac {\sqrt {3}}{2}}$ .

Với một điểm P bất kỳ trong mặt phẳng tam giác, khoảng cách từ nó đến các đỉnh A, B, và C lần lượt là p, q, và t ta có:

3(p^{4}+q^{4}+t^{4}+a^{4})=(p^{2}+q^{2}+t^{2}+a^{2})^{2}

.

Với một điểm P bất kỳ nằm bên trong tam giác, khoảng cách từ nó đến các cạnh tam giác là d, e, và f, thì d+e+f = chiều cao của tam giác, không phụ thuộc vào vị trí P

Với điểm P nằm trên đường tròn ngoại tiếp, các khoảng cách từ nó đến các đỉnh của tam giác là p, q, và t, thì