Sách hình học/Hình/Hình tròn

	Với R - Bán kính vòng tròn D - Đường kính vòng tròn O - Tâm của đường tròn

Chu vi , Diện tích , Thể tích

Chu vi		$P=d\pi =2r\pi$
Diện tích		$S=r^{2}.\pi$ hay $A=(d^{2}.\pi )/4$
Thể tích

Hàm số hình tròn hệ số thực

Hình tròn bán kín Z đơn vị (R=Z)		$X^{2}+Y^{2}=Z^{2}$
Hình tròn bán kín 1 đơn vị (R=1)		$X^{2}+Y^{2}=Z^{2}$ $({\frac {X}{Z}})^{2}+({\frac {Y}{Z}})^{2}=({\frac {Z}{Z}})^{2}$ $\cos ^{2}\theta +\sin ^{2}\theta =1$ $\sec ^{2}\theta -\tan ^{2}\theta =1$ $\sec ^{2}\theta -\tan ^{2}\theta =1$

Hàm số hình tròn hệ số phức

Hình tròn hệ số phức	Hình	Hàm số toán
Hình tròn bán kín Z đơn vị (R=Z)		$Z=X+jY$ $Z=Z(\cos \theta +j\sin \theta )$ $Z=Ze^{j\theta }$
Hình tròn bán kín 1 đơn vị (R=1)		$1={\frac {X+jY}{Z}}$ $1=(\cos \theta +j\sin \theta )$ $1=e^{j\theta }$

Phương trình đường tròn

Phương trình hình tròn hệ số thực

Dạng tổng quát

$X^{2}+Y^{2}=0$

Giải phương trình

$X={\sqrt {-Y^{2}}}=\pm jY$

$Y={\sqrt {-X^{2}}}=\pm jX$

Phương trình hình tròn hệ số phức

Dạng tổng quát

$X+jY=0$

Giải phương trình

$X=-jY$

$jY=-X$

$Y=jX$

Vectơ đường tròn

Đường tròn hệ số thực

${\vec {Z}}={\vec {X}}+{\vec {Y}}=X{\vec {i}}+Y{\vec {j}}=\nabla \cdot {\vec {Z}}+\nabla \times {\vec {Z}}$

${\vec {X}}=X{\vec {i}}=\nabla \cdot {\vec {Z}}$

${\vec {Y}}=Y{\vec {j}}=\nabla \times {\vec {Z}}$

Với

$X=x-x_{o}=\Delta x=Z\cos \theta$

$Y=y-y_{o}=\Delta y=Z\sin \theta$

$Z={\frac {Y}{X}}={\frac {y-y_{o}}{x-x_{o}}}={\frac {\Delta y}{\Delta x}}=Tan\theta$

$\theta =Tan^{-1}{\frac {Y}{X}}$

Đường tròn hệ số thực

$Z=X+jY=z(\cos \theta +j\sin \theta )=ze^{j\theta }$

Cung tròn

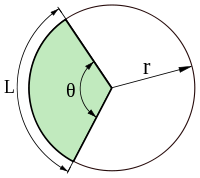
Cung trong hình học (ký hiệu: ⌒) là đoạn đóng của một đường cong khả vi trong một đa tạp. Cung tròn là một phần của đường tròn hay là một phần của chu vi (biên) của hình tròn.

Độ dài cung tròn

Độ dài cung tròn của đường tròn bán kính $r$, chắn góc ở tâm $\theta \,\!$ (đo bằng radian) được tính bằng công thức $\theta r\,\!$. Điều này là vì

${\frac {L}{\mathrm {chuvi} }}={\frac {\theta }{2\pi }}.\,\!$

tương đương

${\frac {L}{2\pi r}}={\frac {\theta }{2\pi }},\,\!$

tương đương

$L=\theta r.\,\!$

Nếu số đo góc ở tâm là $\alpha$ độ thì sẽ có số đo bằng radian là:

$\theta ={\frac {\alpha }{180}}\pi ,\,\!$

Thế vào phương trình trên, thu được công thức tương đương

$L={\frac {\alpha \pi r}{180}}.\,\!$

Một cách thực hành tính độ dài cung tròn là vẽ hai đoạn thẳng từ hai đầu mút giới hạn cung tròn đến tâm đường tròn, đo góc tạo bởi hai đoạn thẳng đó rồi từ đó nhân chéo để tính ra độ dài L:

số đo góc (tính bằng độ)/360 = L/Chuvi.

Ví dụ: cho số đo góc là 60 độ, chu vi là 24 cm

${\frac {60}{360}}={\frac {L}{24}}$

$360L=1440$

$L=4$ (cm).

Diện tích

Diện tích phần giới hạn bởi cung tròn và tâm đường tròn (tức hình quạt tròn) là:

$A={\frac {1}{2}}r^{2}\theta .$

Chia hai vế cho ${\pi r^{2}}$

Tỷ lệ giữa diện tích $A$ và diện tích phần giới hạn trong đường tròn bằng với tỷ lệ giữa số đo góc $\theta$ và số đo góc cả đường tròn

${\frac {A}{\pi r^{2}}}={\frac {\theta }{2\pi }}.$

Giản lược $\pi$ ở cả hai vế

${\frac {A}{r^{2}}}={\frac {\theta }{2}}.$

Nhân hai vế với $r^{2}$, thu được

$A={\frac {1}{2}}r^{2}\theta .$

Tương tự phần trên, công thức tương đương nếu số đo góc đo bằng độ:

$A={\frac {\alpha }{360}}\pi r^{2}.$

Bán kín

Có thể tính được bán kính $r$ của đường tròn nếu biết chiều cao $H$ và chiều rộng $W$ của cung tròn qua việc áp dụng định lý dây cung giao cắt (còn gọi là định lý cát tuyến tiếp tuyến):

Xét dây trương cung của một cung tròn, tạm gọi là dây cung số 1. Đường trung trực của nó là một dây cung khác và là đường kính hình tròn, tạm gọi là dây cung số 2. Dây cung số 1 có độ dài là $W$ và được dây cung số 2 chia làm hai nửa bằng nhau; mỗi phần có độ dài là ${\frac {W}{2}}$. Dây cung số 2 có độ dài $2r$ và được dây cung số 1 chia làm hai phần: một phần gọi là chiều cao cung tròn, ký hiệu là $H$; phần còn lại có độ dài là $(2r-H)$. Áp dụng định lý dây cung giao cắt:

$H(2r-H)=\left({\frac {W}{2}}\right)^{2}$

suy ra:

$2r-H={\frac {W^{2}}{4H}}$

do đó:

$r={\frac {W^{2}}{8H}}+{\frac {H}{2}}.$

Ứng dụng

• Đồ thị Rθ