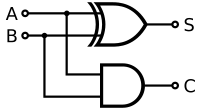Điện giải là phản ứng hóa học giửa hai kim loại và axit tạo ra Điện . Điện giải tạo ra điện không đổi theo thời gian được gọi là Điện DC . Điện giải được dùng tao ra Bình ắc ki cung cấp Điện DC
Phản ứng hóa học giửa kim loại và axit tạo ra Điện . Điện cực tạo ra điện không đổi theo thời gian được gọi là Điện DC
Ứng dụng Điện cực được dùng tao ra Điện DC có điện 1.5 - 3.0 V
[ sửa ]
I
=
Q
t
{\displaystyle I={\frac {Q}{t}}}
Q
=
I
t
{\displaystyle Q=It}
V
=
W
Q
{\displaystyle V={\frac {W}{Q}}}
W
=
Q
V
{\displaystyle W=QV}
E
=
W
t
=
Q
V
t
=
I
V
{\displaystyle E={\frac {W}{t}}={\frac {QV}{t}}=IV}
i
(
t
)
=
d
d
t
Q
(
t
)
{\displaystyle i(t)={\frac {d}{dt}}Q(t)}
Q
(
t
)
=
∫
i
(
t
)
d
t
{\displaystyle Q(t)=\int i(t)dt}
v
(
t
)
=
d
d
t
W
(
t
)
Q
(
t
)
{\displaystyle v(t)={\frac {d}{dt}}{\frac {W(t)}{Q(t)}}}
W
(
t
)
=
∫
v
(
t
)
d
Q
(
t
)
=
∫
v
(
t
)
i
(
t
)
d
t
=
∫
p
(
t
)
d
t
{\displaystyle W(t)=\int v(t)dQ(t)=\int v(t)i(t)dt=\int p(t)dt}
E
=
d
d
t
W
(
t
)
=
d
d
t
∫
p
(
t
)
d
t
{\displaystyle E={\frac {d}{dt}}W(t)={\frac {d}{dt}}\int p(t)dt}
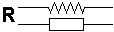
Linh Kiện Điện Tử Điện Trở
Cấu Tạo
Tạo từ một cộng dây dẩn điện thẳng có kích thước
Biểu Tượng
Điện Trở Kháng
R
=
V
I
=
ρ
l
A
{\displaystyle R={\frac {V}{I}}=\rho {\frac {l}{A}}}
Điện Thế
V
=
I
R
{\displaystyle V=IR}
Dòng Điện
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
Điện Trở Kháng và Nhiệt Độ
R
=
R
0
+
n
T
{\displaystyle R=R_{0}+nT}
Dẩn điện
R
=
R
0
e
n
T
{\displaystyle R=R_{0}e^{nT}}
Bán dẩn điện
Điện Trở Kháng và Năng Lượng Điện
P
R
=
i
2
R
(
T
)
{\displaystyle P_{R}=i^{2}R(T)}
Năng Lượng Điện Phát
P
V
=
i
v
{\displaystyle P_{V}=iv}
Năng Lượng Điện Truyền
P
=
P
V
−
P
R
=
i
v
−
i
2
R
(
T
)
=
i
[
v
−
i
R
(
T
)
]
{\displaystyle P=P_{V}-P_{R}=iv-i^{2}R(T)=i[v-iR(T)]}
Hiệu Thế Điện Truyền
n
=
P
P
V
=
v
−
i
R
(
T
)
v
=
1
−
i
R
(
T
)
v
{\displaystyle n={\frac {P}{P_{V}}}={\frac {v-iR(T)}{v}}=1-{\frac {iR(T)}{v}}}
Điện Kháng
Z
R
=
R
+
X
R
{\displaystyle Z_{R}=R+X_{R}}
Z
R
=
R
∠
0
o
=
R
{\displaystyle Z_{R}=R\angle 0^{o}=R}
Điện Ứng
X
R
=
0
{\displaystyle X_{R}=0}
Góc độ khác biệt
θ
=
0
{\displaystyle \theta =0}
Phản ứng tần số
Không phụ thuộc vào tần số
Linh Kiện Điện Tử Điện Trở
Cấu Tạo
Tạo từ một cộng dây dẩn điện có kích thước
Biểu Tượng
Từ Dung
L
=
B
I
=
μ
N
2
l
{\displaystyle L={\frac {B}{I}}=\mu {\frac {N^{2}}{l}}}
Dòng Điện
I
=
B
L
{\displaystyle I={\frac {B}{L}}}
Cảm từ
B
=
L
I
=
μ
N
2
I
l
{\displaystyle B=LI=\mu {\frac {N^{2}I}{l}}}
Điện Thế
v
(
t
)
=
L
d
i
(
t
)
d
t
{\displaystyle v(t)=L{\frac {di(t)}{dt}}}
Dòng Điện
i
(
t
)
=
1
L
∫
v
(
t
)
d
t
{\displaystyle i(t)={\frac {1}{L}}\int v(t)dt}
Năng Lượng Điện thất thoát dưới dạng nhiệt
P
(
t
)
=
∫
B
d
i
=
∫
L
i
d
i
=
1
2
L
i
2
{\displaystyle P(t)=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}}
Điện Kháng
Z
L
=
v
L
i
L
=
R
L
+
X
L
{\displaystyle Z_{L}={\frac {v_{L}}{i_{L}}}=R_{L}+X_{L}}
Z
L
=
R
∠
0
+
ω
L
∠
90
{\displaystyle Z_{L}=R\angle 0+\omega L\angle 90}
Z
L
=
R
+
j
ω
L
{\displaystyle Z_{L}=R+j\omega L}
Z
L
=
R
+
s
L
{\displaystyle Z_{L}=R+sL}
Điện Ứng
X
L
=
ω
L
∠
90
{\displaystyle X_{L}=\omega L\angle 90}
X
L
=
j
ω
L
{\displaystyle X_{L}=j\omega L}
X
L
=
s
L
{\displaystyle X_{L}=sL}
Góc độ khác biệt
T
a
n
θ
=
ω
T
{\displaystyle Tan\theta =\omega T}
Hằng số thời gian
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
Phản Ứng Tần Số
Đóng mạch ở tần số thấp . Hở mạch ở tần số cao cuộn từ không có thất thóat
Linh Kiện Điện Tử Tụ điện
Cấu Tạo
Tạo từ 2 bề mặt dẩn điện có kích thước
Biểu Tượng
Điện dung
C
=
Q
V
=
ϵ
A
l
{\displaystyle C={\frac {Q}{V}}=\epsilon {\frac {A}{l}}}
Điện thế
V
=
Q
C
=
W
Q
=
E
d
{\displaystyle V={\frac {Q}{C}}={\frac {W}{Q}}=Ed}
Điện tích
Q
=
C
V
{\displaystyle Q=CV}
Dòng điện
I
=
Q
t
{\displaystyle I={\frac {Q}{t}}}
Năng lượng
P
=
W
t
=
W
Q
Q
t
=
i
v
{\displaystyle P={\frac {W}{t}}={\frac {W}{Q}}{\frac {Q}{t}}=iv}
Điện Thế
v
(
t
)
=
1
C
∫
i
(
t
)
d
t
{\displaystyle v(t)={\frac {1}{C}}\int i(t)dt}
Dòng Điện
i
(
t
)
=
C
d
v
(
t
)
d
t
{\displaystyle i(t)=C{\frac {dv(t)}{dt}}}
Năng Lượng Điện thất thoát dưới dạng nhiệt
P
(
t
)
=
∫
Q
(
t
)
d
t
=
∫
L
i
d
i
=
1
2
L
i
2
{\displaystyle P(t)=\int Q(t)dt=\int Lidi={\frac {1}{2}}Li^{2}}
Điện Kháng
Z
C
=
R
C
+
X
C
{\displaystyle Z_{C}=R_{C}+X_{C}}
Z
C
=
R
∠
0
+
1
ω
C
∠
−
90
{\displaystyle Z_{C}=R\angle 0+{\frac {1}{\omega C}}\angle -90}
Z
C
=
R
+
1
j
ω
C
{\displaystyle Z_{C}=R+{\frac {1}{j\omega C}}}
Z
C
=
R
+
1
s
C
{\displaystyle Z_{C}=R+{\frac {1}{sC}}}
Điện Ứng
X
C
=
1
ω
C
∠
−
90
=
1
j
ω
C
=
1
s
C
{\displaystyle X_{C}={\frac {1}{\omega C}}\angle -90={\frac {1}{j\omega C}}={\frac {1}{sC}}}
Góc độ khác biệt
T
a
n
θ
=
1
ω
T
{\displaystyle Tan\theta ={\frac {1}{\omega T}}}
Hằng số thời gian
T
=
R
C
{\displaystyle T=RC}
Phản Ứng Tần Số
Đóng mạch ở tần số cao . Hở mạch ở tần số thấp tụ điện không có thất thóat
Mạch điện điện tử là một vòng khép kín của nhiều linh kiện điện tử mắc nối với nhau
Hoán chuyển mạch điện Thevenin
Hoán chuyển mạch điện Norton
Định luật Kirchhoff về cường độ dòng điện
∑
k
=
1
n
I
k
=
0
{\displaystyle \sum _{k=1}^{n}{I}_{k}=0}
Định luật Kirchhoff về điện thế
∑
k
=
1
n
V
k
=
0
{\displaystyle \sum _{k=1}^{n}V_{k}=0}
I
t
=
I
1
=
I
2
=
.
.
.
=
I
n
{\displaystyle I_{t}=I_{1}=I_{2}=...=I_{n}}
R
t
=
V
I
t
=
V
1
I
1
+
V
2
I
2
+
.
.
.
+
V
n
I
n
{\displaystyle R_{t}={\frac {V}{I_{t}}}={\frac {V_{1}}{I_{1}}}+{\frac {V_{2}}{I_{2}}}+...+{\frac {V_{n}}{I_{n}}}}
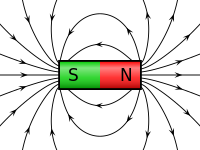
Nam châm là một vật liệu hoặc vật thể tạo ra từ trường. Từ trường này vô hình và có khả năng tạo ra lực từ hút các vật liệu kim loại như sắt nằm kề bên nam châm . Có 2 loại Nam châm là Nam châm thường và Nam châm điện
Loại nam châm Cấu tạo
Nam châm thừong
Nam châm điện
Mọi Nam châm đều có 2 cực , Cực bác[N] và Cực nam[S] . Từ trường tạo ra từ các đường sức lực (Lực từ) đi từ cực bắc đến cực nam có khả năng hút vật liệu từ như Sắt, Nam châm khác về hướng mình
Điện tích đại diện cho các phần tử mang điện tồn tại trong tự nhiên thí dụ như điện tử âm, điện tử dương, điện tử trng hòa trong nguyên tử điện . Điện tích còn được hiểu là "vật tích điện". Mọi vật trung hòa về điện khi cho hay nhận điện tử âm sẽ trở thành điện tích. Khi vật nhận electron vật sẻ trở thành điện tích âm . Khi vật cho electron vật sẻ trở thành điện tích dương
Loại điện tích 'Ký hiệu
Tích điện của vật Điện trường Từ trường
Điện tích âm
(-)
Vật + e
Điện tích dương
(+)
Vật − e
Điện trường của điện tích điểm dương và âm. Lực điện tích âm hút điện tích dương về hướng mình được tính bằng định luật Coulomb như sau
F
Q
=
K
Q
+
Q
−
r
2
{\displaystyle F_{Q}=K{\frac {Q_{+}Q_{-}}{r^{2}}}}
Với 2 điện lượng cùng cường độ
Q
+
=
Q
−
=
Q
{\displaystyle Q_{+}=Q_{-}=Q}
Lự Coulomb
F
Q
=
K
Q
2
r
2
{\displaystyle F_{Q}=K{\frac {Q^{2}}{r^{2}}}}
Khoảng cách giửa 2 điện tích
r
=
K
Q
2
F
Q
{\displaystyle r={\sqrt {K{\frac {Q^{2}}{F_{Q}}}}}}
Điện trường
E
=
F
Q
Q
=
K
Q
r
2
{\displaystyle E={\frac {F_{Q}}{Q}}=K{\frac {Q}{r^{2}}}}
Năng lực Điện trường
W
E
=
∫
E
d
r
=
∫
K
Q
r
2
d
r
=
K
Q
r
{\displaystyle W_{E}=\int Edr=\int K{\frac {Q}{r^{2}}}dr=K{\frac {Q}{r}}}
Năng lươ.ng Điện trường
U
E
=
W
E
t
=
K
Q
r
t
{\displaystyle U_{E}={\frac {W_{E}}{t}}=K{\frac {Q}{rt}}}
Thí nghiệm cho thây, lực điện tương tác với điện tích làm cho điện tích di chuyển thẳng hàng theo hướng ngang sẻ tạo ra một điện trường . Lực điện tạo ra điện trường được tính theo định luật Ampere như sau
F
E
=
Q
E
{\displaystyle F_{E}=QE}
Từ trên,
F
E
=
Q
E
=
Q
V
l
=
W
l
{\displaystyle F_{E}=QE=Q{\frac {V}{l}}={\frac {W}{l}}}
Đường dài di chuyển
l
=
W
F
E
{\displaystyle l={\frac {W}{F_{E}}}}
Vận tốc di chuyển
v
=
l
t
=
W
t
F
E
=
U
F
E
{\displaystyle v={\frac {l}{t}}={\frac {W}{tF_{E}}}={\frac {U}{F_{E}}}}
Thời gian di chuyển
t
=
l
v
=
W
F
E
/
U
F
E
=
W
U
{\displaystyle t={\frac {l}{v}}={\frac {W}{F_{E}}}/{\frac {U}{F_{E}}}={\frac {W}{U}}}
Thí nghiệm cho thấy, khi điện tích di chuyển qua nam châm, lực từ của nam châm làm cho điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống hoặc theo vòng tròn quỹ đạo đi thuận hay nghịch chiều kim đồng hồ
Điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống Trong trường hợp lực từ của nam châm làm cho điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống . Lực từ được tính theo định luật Lorentz như sau
F
B
=
±
Q
v
B
{\displaystyle F_{B}=\pm QvB}
Với
F
B
{\displaystyle F_{B}}
Q
{\displaystyle Q}
v
{\displaystyle v}
B
{\displaystyle B}
Từ trên,
F
B
=
Q
v
B
=
I
t
v
B
=
I
l
B
{\displaystyle F_{B}=QvB=ItvB=IlB}
Vận tốc di chuyển
v
=
F
B
Q
B
{\displaystyle v={\frac {F_{B}}{QB}}}
Đường dài di chuyển
l
=
F
B
I
B
{\displaystyle l={\frac {F_{B}}{IB}}}
Thời gian di chuyển
t
=
F
B
I
B
/
F
B
Q
B
=
Q
I
{\displaystyle t={\frac {F_{B}}{IB}}/{\frac {F_{B}}{QB}}={\frac {Q}{I}}}
Điện tích di chuyển theo vòng tròn quỹ đạo đi thuận hay nghịch chiều kim đồng hồ Chuyểng động cân bằng của 2 lực lực vô vòng tròn và lực từ động
F
R
=
F
B
{\displaystyle F_{R}=F_{B}}
m
v
2
R
=
Q
v
B
{\displaystyle {\frac {mv^{2}}{R}}=QvB}
Vận tốc di chuyển
v
=
Q
m
B
R
{\displaystyle v={\frac {Q}{m}}BR}
Bán kín vòng tròn
R
=
m
v
Q
B
{\displaystyle R={\frac {mv}{QB}}}
Lực Điện từ Lực điện từ có ký hiệu
F
E
B
{\displaystyle F_{EB}}
N . Lực điện từ tạo ra từ tổng của 2 lực , Lực động điện và Lực động từ được tính bằng công thức sau
F
E
B
=
F
E
+
F
B
=
Q
E
±
Q
v
B
=
Q
(
E
±
v
B
)
{\displaystyle F_{EB}=F_{E}+F_{B}=QE\pm QvB=Q(E\pm vB)}
Với
F
E
B
{\displaystyle F_{EB}}
F
E
{\displaystyle F_{E}}
F
B
{\displaystyle F_{B}}
Q
{\displaystyle Q}
E
{\displaystyle E}
E
{\displaystyle E}
v
{\displaystyle v}
Từ trên,
v
=
0
{\displaystyle v=0}
F
E
B
=
Q
E
{\displaystyle F_{EB}=QE}
Q
,
E
=
0
{\displaystyle Q,E=0}
F
E
B
=
±
Q
v
B
{\displaystyle F_{EB}=\pm QvB}
E
±
Q
v
B
=
0
{\displaystyle E\pm QvB=0}
F
E
B
=
Q
(
E
±
v
B
)
=
0
{\displaystyle F_{EB}=Q(E\pm vB)=0}
E
±
Q
v
B
=
0
{\displaystyle E\pm QvB=0}
|
E
|
=
v
|
B
|
{\displaystyle |E|=v|B|}
|
B
|
=
1
v
|
E
|
{\displaystyle |B|={\frac {1}{v}}|E|}
v
=
|
E
|
|
B
|
{\displaystyle v={\frac {|E|}{|B|}}}
Đường dài điện trường
l
E
=
Q
V
F
E
{\displaystyle l_{E}={\frac {QV}{F_{E}}}}
Đường dài từ trường
l
B
=
F
B
I
B
{\displaystyle l_{B}={\frac {F_{B}}{IB}}}
Đường dài điện từ trường
l
E
B
=
l
E
2
+
l
B
2
=
(
Q
V
F
E
)
2
+
(
F
B
I
B
)
2
{\displaystyle l_{EB}={\sqrt {l_{E}^{2}+l_{B}^{2}}}={\sqrt {({\frac {QV}{F_{E}}})^{2}+({\frac {F_{B}}{IB}})^{2}}}}
Cho biết cách tính mật độ trường điện từ
ΨE = EA =
∮
S
E
⋅
d
A
=
1
ϵ
o
∫
V
ρ
d
V
=
Q
A
ϵ
o
{\displaystyle \oint _{S}\mathbf {E} \cdot d\mathbf {A} ={1 \over \epsilon _{o}}\int _{V}\rho \ dV={\frac {Q_{A}}{\epsilon _{o}}}}
ΨE = BA =
∮
S
B
⋅
d
s
=
μ
0
I
e
n
c
{\displaystyle \oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }}
Φ
{\displaystyle \Phi }
thông lượng điện ,
E
{\displaystyle \mathbf {E} }
điện trường ,
d
A
{\displaystyle d\mathbf {A} }
S ,
Q
A
{\displaystyle Q_{\mathrm {A} }}
ρ
{\displaystyle \rho }
V
{\displaystyle V}
ϵ
o
{\displaystyle \epsilon _{o}}
hằng số điện của không gian tự do và
∮
S
{\displaystyle \oint _{S}}
S bao phủ thể tích V .Cho biết cách tính cường độ từ cảm của dẩn điện
B
=
μ
A
i
=
L
i
{\displaystyle B={\frac {\mu }{A}}i=Li}
Cho biết cách tính cường độ từ nhiểm của từ vật
H
=
B
μ
{\displaystyle H={\frac {B}{\mu }}}
Cho biết cách tính cường độ từ cảm ứng của dẩn điện
−
ϕ
B
=
−
N
B
=
−
N
L
i
{\displaystyle -\phi _{B}=-NB=-NLi}
Cho biết cách tính cường độ điện từ cảm ứng của dẩn điện
−
ϵ
=
−
∫
E
d
l
=
−
d
ϕ
B
d
t
{\displaystyle -\epsilon =-\int Edl=-{\frac {d\phi _{B}}{dt}}}
[ sửa ]
∮
C
H
⋅
d
l
=
∬
S
J
⋅
d
A
+
d
d
t
∬
S
D
⋅
d
A
{\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} \mathbf {l} =\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {A} +{\mathrm {d} \over \mathrm {d} t}\iint _{S}\mathbf {D} \cdot \mathrm {d} \mathbf {A} }
∮
S
B
⋅
d
s
=
μ
0
I
e
n
c
+
d
Φ
E
d
t
{\displaystyle \oint _{S}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I_{\mathrm {enc} }+{\frac {d\mathbf {\Phi _{E}} }{dt}}}
Từ trên
Q
=
ϵ
E
A
=
D
A
{\displaystyle Q=\epsilon EA=DA}
D
=
ϵ
E
=
Q
A
{\displaystyle D=\epsilon E={\frac {Q}{A}}}
E
=
D
ϵ
=
Q
ϵ
A
{\displaystyle E={\frac {D}{\epsilon }}={\frac {Q}{\epsilon A}}}
ϵ
=
D
E
=
Q
E
{\displaystyle \epsilon ={\frac {D}{E}}={\frac {Q}{E}}}
I
=
B
A
μ
=
H
A
{\displaystyle I={\frac {BA}{\mu }}=HA}
B
=
μ
I
A
=
L
I
{\displaystyle B={\frac {\mu I}{A}}=LI}
H
=
B
μ
=
I
A
{\displaystyle H={\frac {B}{\mu }}={\frac {I}{A}}}
μ
=
B
A
I
=
B
H
{\displaystyle \mu ={\frac {BA}{I}}={\frac {B}{H}}}
D
=
H
{\displaystyle D=H}
ϵ
E
=
B
μ
{\displaystyle \epsilon E={\frac {B}{\mu }}}
1
μ
ϵ
=
E
B
{\displaystyle {\sqrt {\frac {1}{\mu \epsilon }}}={\sqrt {\frac {E}{B}}}}
C
2
=
E
B
{\displaystyle C^{2}={\frac {E}{B}}}
E
=
C
2
B
{\displaystyle E=C^{2}B}
B
=
1
C
2
E
{\displaystyle B={\frac {1}{C^{2}}}E}
[ sửa ] [ sửa ]
Cộng dây thẳng dẩn điện
B
=
L
i
=
μ
A
i
=
2
π
r
l
i
{\displaystyle B=Li={\frac {\mu }{A}}i={\frac {2\pi r}{l}}i}
H
=
B
μ
=
2
π
r
μ
l
i
{\displaystyle H={\frac {B}{\mu }}={\frac {2\pi r}{\mu l}}i}
B
=
L
i
=
μ
A
i
=
2
π
l
i
{\displaystyle B=Li={\frac {\mu }{A}}i={\frac {2\pi }{l}}i}
H
=
B
μ
=
2
π
μ
l
i
{\displaystyle H={\frac {B}{\mu }}={\frac {2\pi }{\mu l}}i}
B
=
L
i
=
N
μ
A
i
{\displaystyle B=Li={\frac {N\mu }{A}}i}
H
=
B
μ
=
N
i
A
{\displaystyle H={\frac {B}{\mu }}={\frac {Ni}{A}}}
[ sửa ]
Dẩn điện Từ trường - B Từ dung - L
Cộng dây thẳng dẩn điện
B
=
L
I
=
μ
A
I
=
2
π
r
l
I
{\displaystyle B=LI={\frac {\mu }{A}}I={\frac {2\pi r}{l}}I}
L
=
B
I
=
2
π
r
l
{\displaystyle L={\frac {B}{I}}={\frac {2\pi r}{l}}}
B
=
L
I
=
μ
A
I
=
2
π
l
I
{\displaystyle B=LI={\frac {\mu }{A}}I={\frac {2\pi }{l}}I}
L
=
B
I
=
2
π
l
{\displaystyle L={\frac {B}{I}}={\frac {2\pi }{l}}}
B
=
L
I
=
μ
A
I
=
N
μ
l
I
{\displaystyle B=LI={\frac {\mu }{A}}I={\frac {N\mu }{l}}I}
L
=
B
I
=
N
μ
l
{\displaystyle L={\frac {B}{I}}={\frac {N\mu }{l}}}
Với cuộn từ có N vòng tròn từ
−
ϕ
B
=
−
N
B
=
−
N
L
i
{\displaystyle -\phi _{B}=-NB=-NLi}
Với cuộn từ có 1 vòng tròn từ
−
ϕ
B
=
−
N
B
=
−
L
i
{\displaystyle -\phi _{B}=-NB=-Li}
Với cuộn từ có N vòng tròn từ
−
ϵ
=
−
d
ϕ
B
d
t
=
−
N
L
d
i
d
t
{\displaystyle -\epsilon =-{\frac {d\phi _{B}}{dt}}=-NL{\frac {di}{dt}}}
Với cuộn từ có 1 vòng tròn từ
−
ϵ
=
−
d
ϕ
B
d
t
=
−
L
d
i
d
t
{\displaystyle -\epsilon =-{\frac {d\phi _{B}}{dt}}=-L{\frac {di}{dt}}}
[ sửa ] [ sửa ] Các phương trình Maxwell bao gồm bốn phương trình , đề ra bởi James Clerk Maxwell , dùng để mô tả trường điện từ cũng như những tương tác của chúng đối với vật chất.
Bốn phương trình Maxwell mô tả lần lượt:
Tên
Dạng phương trình vi phân
Dạng tích phân
Định luật Gauss :
∇
⋅
D
=
ρ
{\displaystyle \nabla \cdot \mathbf {D} =\rho }
∮
S
D
⋅
d
A
=
∫
V
ρ
d
V
{\displaystyle \oint _{S}\mathbf {D} \cdot d\mathbf {A} =\int _{V}\rho dV}
Đinh luật Gauss cho từ trường từ tích ):
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0}
∮
S
B
⋅
d
A
=
0
{\displaystyle \oint _{S}\mathbf {B} \cdot d\mathbf {A} =0}
Định luật Faraday cho từ trường :
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
∮
C
E
⋅
d
l
=
−
d
d
t
∫
S
B
⋅
d
A
{\displaystyle \oint _{C}\mathbf {E} \cdot d\mathbf {l} =-\ {d \over dt}\int _{S}\mathbf {B} \cdot d\mathbf {A} }
Định luật Ampere Maxwell ):
∇
×
H
=
J
+
∂
D
∂
t
{\displaystyle \nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}}
∮
C
H
⋅
d
l
=
∫
S
J
⋅
d
A
+
d
d
t
∫
S
D
⋅
d
A
{\displaystyle \oint _{C}\mathbf {H} \cdot d\mathbf {l} =\int _{S}\mathbf {J} \cdot d\mathbf {A} +{d \over dt}\int _{S}\mathbf {D} \cdot d\mathbf {A} }
[ sửa ] Được biểu diển bởi Laplace
Vector trường điện từ trong chân không
H
=
0
{\displaystyle H=0}
∇
⋅
E
=
0
{\displaystyle \nabla \cdot \mathbf {E} =0}
∇
×
E
=
−
1
T
o
E
{\displaystyle \nabla \times \mathbf {E} =-{\frac {1}{T_{o}}}\mathbf {E} }
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0}
∇
×
B
=
−
1
T
o
E
{\displaystyle \nabla \times \mathbf {B} =-{\frac {1}{T_{o}}}\mathbf {E} }
T
o
=
μ
ϵ
{\displaystyle T_{o}=\mu \epsilon }
Phương trình hàm số Sóng Điện từ
∇
2
E
=
−
β
o
E
{\displaystyle \nabla ^{2}E=-\beta _{o}\mathbf {E} }
∇
2
B
=
−
β
o
E
{\displaystyle \nabla ^{2}B=-\beta _{o}\mathbf {E} }
Hàm số Sóng Điện từ
E
=
A
s
i
n
ω
o
t
{\displaystyle E=Asin\omega _{o}t}
B
=
A
s
i
n
ω
o
t
{\displaystyle B=Asin\omega _{o}t}
ω
o
=
β
o
{\displaystyle \omega _{o}={\sqrt {\beta _{o}}}}
Vector trường điện từ trong môi trường vật chất
H ≠ 0
∇
⋅
E
=
0
{\displaystyle \nabla \cdot \mathbf {E} =0}
∇
×
E
=
−
1
T
E
{\displaystyle \nabla \times \mathbf {E} =-{\frac {1}{T}}\mathbf {E} }
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0}
∇
×
B
=
−
1
T
E
{\displaystyle \nabla \times \mathbf {B} =-{\frac {1}{T}}\mathbf {E} }
T
=
μ
ϵ
{\displaystyle T=\mu \epsilon }
Phương trình hàm số Sóng Điện từ
∇
2
E
=
−
β
E
{\displaystyle \nabla ^{2}E=-\beta \mathbf {E} }
∇
2
B
=
−
β
E
{\displaystyle \nabla ^{2}B=-\beta \mathbf {E} }
Hàm số Sóng Điện từ
E
=
A
s
i
n
ω
t
{\displaystyle E=Asin\omega t}
B
=
A
s
i
n
ω
t
{\displaystyle B=Asin\omega t}
ω
=
β
{\displaystyle \omega ={\sqrt {\beta }}}
[ sửa ] Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường , E và Từ trường , B
∇
⋅
E
=
0
{\displaystyle \nabla \cdot E=0}
∇
×
E
=
−
1
T
E
{\displaystyle \nabla \times E=-{\frac {1}{T}}E}
∇
⋅
B
=
0
{\displaystyle \nabla \cdot B=0}
∇
×
B
=
−
1
T
B
{\displaystyle \nabla \times B=-{\frac {1}{T}}B}
T
=
μ
ϵ
{\displaystyle T=\mu \epsilon }
Dao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường , E và Từ trường , B
∇
⋅
E
=
0
{\displaystyle \nabla \cdot E=0}
∇
×
E
=
−
1
T
E
{\displaystyle \nabla \times E=-{\frac {1}{T}}E}
∇
⋅
B
=
0
{\displaystyle \nabla \cdot B=0}
∇
×
B
=
−
1
T
B
{\displaystyle \nabla \times B=-{\frac {1}{T}}B}
T
=
μ
ϵ
{\displaystyle T=\mu \epsilon }
Dùng phép toán
∇
(
∇
×
E
)
=
∇
(
−
1
T
E
)
=
∇
2
E
{\displaystyle \nabla (\nabla \times E)=\nabla (-{\frac {1}{T}}E)=\nabla ^{2}E}
∇
(
∇
×
B
)
=
∇
(
−
1
T
B
)
=
∇
2
B
{\displaystyle \nabla (\nabla \times B)=\nabla (-{\frac {1}{T}}B)=\nabla ^{2}B}
[ sửa ] Cho một Phương trình sóng điện từ
∇
2
E
=
−
β
E
{\displaystyle \nabla ^{2}E=-\beta E}
∇
2
B
=
−
β
B
{\displaystyle \nabla ^{2}B=-\beta B}
β
=
1
T
{\displaystyle \beta ={\frac {1}{T}}}
Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ
E
=
A
s
i
n
ω
t
{\displaystyle E=Asin\omega t}
B
=
A
s
i
n
ω
t
{\displaystyle B=Asin\omega t}
ω
=
λ
f
=
β
=
C
=
3
×
10
8
{\displaystyle \omega =\lambda f={\sqrt {\beta }}=C=3\times 10^{8}}
[ sửa ] [ sửa ]
v
=
ω
=
λ
f
=
1
μ
ϵ
=
C
{\displaystyle v=\omega =\lambda f={\sqrt {\frac {1}{\mu \epsilon }}}=C}
W
=
p
v
=
p
C
=
p
λ
f
=
h
f
{\displaystyle W=pv=pC=p\lambda f=hf}
Với
h
=
p
λ
{\displaystyle h=p\lambda }
Một đại lượng không có khối lượng và có giá trị là một hằng số không đổi
h
=
p
λ
{\displaystyle h=p\lambda }
Lượng tử có lưởng tính Sóng Hạt . Lưởng tính Sóng - Hạt cho phép lượng tử di chuyển dưới dạng Sóng điện từ và truyền năng lượng dưới dạng Hạt
λ
=
h
p
{\displaystyle \lambda ={\frac {h}{p}}}
p
=
h
λ
{\displaystyle p={\frac {h}{\lambda }}}
Có 2 loại lượng được tìm thấy là Lượng tử quang ở
f
=
f
o
{\displaystyle f=f_{o}}
f
>
f
o
{\displaystyle f>f_{o}}
h
=
p
λ
o
=
p
C
f
o
{\displaystyle h=p\lambda _{o}=p{\frac {C}{f_{o}}}}
h
=
p
λ
=
p
C
f
{\displaystyle h=p\lambda =p{\frac {C}{f}}}
[ sửa ] Mọi lượng tử đều có một năng lực lượng tử tính bằng
W
=
h
f
=
h
C
λ
{\displaystyle W=hf=h{\frac {C}{\lambda }}}
Năng lực lượng tử được tìm thấy ở 2 trạng thái Năng lực lượng tử quang ở
f
=
f
o
{\displaystyle f=f_{o}}
f
>
f
o
{\displaystyle f>f_{o}}
Năng lực lượng tử quang
W
o
=
h
f
o
=
h
C
λ
o
{\displaystyle W_{o}=hf_{o}=h{\frac {C}{\lambda _{o}}}}
Năng lực lượng tử điện
W
=
h
f
=
h
C
λ
{\displaystyle W=hf=h{\frac {C}{\lambda }}}
Xác xuất tìm thấy Năng lực lượng tử của lượng tử được phát biểu trong Định luật Heinseinberg
Năng lực lượng tử chỉ có thể tìm thấy ở 1 trong 2 trạng thái Năng lực lượng tử quang hay Năng lực lượng tử điện Có thể biểu diển bằng công thức toán
1
2
h
{\displaystyle {\frac {1}{2}}h}
[ sửa ] Phóng xạ sóng điện từ có phổ tần phóng xạ sau
RF , Sóng tần số radioVF , Ánh sáng thấy đượcUVF , Ánh sáng tímX , Tia Xγ , Tia gamma
V
=
I
R
{\displaystyle V=IR}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
R
=
V
I
=
ρ
l
A
{\displaystyle R={\frac {V}{I}}=\rho {\frac {l}{A}}}
G
=
I
V
=
1
R
=
σ
A
l
{\displaystyle G={\frac {I}{V}}={\frac {1}{R}}=\sigma {\frac {A}{l}}}
ρ
=
V
I
A
l
=
R
A
l
{\displaystyle \rho ={\frac {V}{I}}{\frac {A}{l}}=R{\frac {A}{l}}}
σ
=
I
V
l
A
=
G
l
A
{\displaystyle \sigma ={\frac {I}{V}}{\frac {l}{A}}=G{\frac {l}{A}}}
Điện ứng, Điện kháng
v
(
t
)
=
i
(
t
)
X
(
t
)
{\displaystyle v(t)=i(t)X(t)}
i
(
t
)
=
v
(
t
)
X
(
t
)
=
0
{\displaystyle i(t)={\frac {v(t)}{X(t)}}=0}
X
(
t
)
=
v
(
t
)
i
(
t
)
=
0
{\displaystyle X(t)={\frac {v(t)}{i(t)}}=0}
Z
(
t
)
=
R
+
X
(
t
)
=
R
∠
0
,
R
,
R
{\displaystyle Z(t)=R+X(t)=R\angle 0,R,R}
Điện từ
B
=
L
i
=
μ
2
π
r
i
{\displaystyle B=Li={\frac {\mu }{2\pi r}}i}
L
=
B
i
=
μ
2
π
r
{\displaystyle L={\frac {B}{i}}={\frac {\mu }{2\pi r}}}
Điện nhiệt từ
W
i
=
i
2
R
(
T
)
{\displaystyle W_{i}=i^{2}R(T)}
R
(
T
)
=
R
o
+
n
T
{\displaystyle R(T)=R_{o}+nT}
R
(
T
)
=
R
o
e
n
T
{\displaystyle R(T)=R_{o}e^{nT}}
W
e
=
p
v
=
m
C
Δ
T
{\displaystyle W_{e}=pv=mC\Delta T}
B
=
L
I
{\displaystyle B=LI}
I
=
B
L
{\displaystyle I={\frac {B}{L}}}
L
=
B
I
=
N
μ
o
l
{\displaystyle L={\frac {B}{I}}={\frac {N\mu _{o}}{l}}}
v
(
t
)
=
L
d
i
(
t
)
d
t
{\displaystyle v(t)=L{\frac {di(t)}{dt}}}
i
(
t
)
=
1
L
∫
v
(
t
)
d
t
{\displaystyle i(t)={\frac {1}{L}}\int v(t)dt}
X
(
t
)
=
v
(
t
)
i
(
t
)
=
ω
L
∠
90
=
j
ω
L
=
s
L
{\displaystyle X(t)={\frac {v(t)}{i(t)}}=\omega L\angle 90=j\omega L=sL}
Z
(
t
)
=
R
+
X
(
t
)
=
R
∠
0
+
ω
L
∠
90
=
R
+
j
ω
L
=
R
+
s
L
{\displaystyle Z(t)=R+X(t)=R\angle 0+\omega L\angle 90=R+j\omega L=R+sL}
B
=
L
i
=
N
μ
o
l
i
{\displaystyle B=Li={\frac {N\mu _{o}}{l}}i}
L
=
B
L
=
i
=
N
μ
o
l
{\displaystyle L={\frac {B}{L}}=i={\frac {N\mu _{o}}{l}}}
W
i
=
∫
B
d
i
=
∫
L
i
d
i
=
1
2
L
i
2
{\displaystyle W_{i}=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}}
W
e
=
p
v
=
p
ω
o
=
p
λ
o
f
o
=
h
f
o
{\displaystyle W_{e}=pv=p\omega _{o}=p\lambda _{o}f_{o}=hf_{o}}
W
e
=
p
v
=
p
ω
o
=
p
1
μ
o
ϵ
o
=
p
C
{\displaystyle W_{e}=pv=p\omega _{o}=p{\sqrt {\frac {1}{\mu _{o}\epsilon _{o}}}}=pC}
W
e
=
p
C
=
h
f
o
{\displaystyle W_{e}=pC=hf_{o}}
Q
=
C
V
{\displaystyle Q=CV}
V
=
Q
C
{\displaystyle V={\frac {Q}{C}}}
C
=
Q
V
=
ϵ
A
l
{\displaystyle C={\frac {Q}{V}}=\epsilon {\frac {A}{l}}}
v
(
t
)
=
1
C
∫
i
(
t
)
d
t
{\displaystyle v(t)={\frac {1}{C}}\int i(t)dt}
i
(
t
)
=
C
d
v
(
t
)
d
t
{\displaystyle i(t)=C{\frac {dv(t)}{dt}}}
X
(
t
)
=
v
(
t
)
i
(
t
)
=
1
ω
C
∠
−
90
=
1
j
ω
C
=
1
s
C
{\displaystyle X(t)={\frac {v(t)}{i(t)}}={\frac {1}{\omega C}}\angle -90={\frac {1}{j\omega C}}={\frac {1}{sC}}}
Z
(
t
)
=
R
+
X
(
t
)
=
R
∠
0
+
1
ω
C
∠
−
90
=
R
+
1
j
ω
C
=
R
+
1
s
C
{\displaystyle Z(t)=R+X(t)=R\angle 0+{\frac {1}{\omega C}}\angle -90=R+{\frac {1}{j\omega C}}=R+{\frac {1}{sC}}}
B
=
L
i
=
N
μ
l
i
{\displaystyle B=Li={\frac {N\mu }{l}}i}
L
=
B
L
=
i
=
N
μ
l
{\displaystyle L={\frac {B}{L}}=i={\frac {N\mu }{l}}}
W
i
=
∫
B
d
i
=
∫
L
i
d
i
=
1
2
L
i
2
{\displaystyle W_{i}=\int Bdi=\int Lidi={\frac {1}{2}}Li^{2}}
W
e
=
p
v
=
p
ω
=
p
λ
f
=
h
f
{\displaystyle W_{e}=pv=p\omega =p\lambda f=hf}
W
e
=
p
v
=
p
ω
=
p
1
μ
ϵ
=
p
C
{\displaystyle W_{e}=pv=p\omega =p{\sqrt {\frac {1}{\mu \epsilon }}}=pC}
W
e
=
p
C
=
h
f
{\displaystyle W_{e}=pC=hf}
Mạch điện điện tử là một vòng khép kín của nhiều linh kiện điện tử mắc nối với nhau theo một định hình liệt kê dưới đây
[ sửa ]
Mạch Điện
RLC Nối Tiếp
Lối Mắc
Phương Trình Đạo Hàm
L
d
i
d
t
+
1
C
∫
i
d
t
+
i
R
=
0
{\displaystyle L{\frac {di}{dt}}+{\frac {1}{C}}\int idt+iR=0}
d
2
i
d
t
+
R
L
d
i
d
t
+
1
L
C
i
=
0
{\displaystyle {\frac {d^{2}i}{dt}}+{\frac {R}{L}}{\frac {di}{dt}}+{\frac {1}{LC}}i=0}
s
2
i
+
2
α
s
i
+
β
i
=
0
{\displaystyle s^{2}i+2\alpha si+\beta i=0}
Giá trị s
s
=
−
α
{\displaystyle s=-\alpha }
α
=
β
{\displaystyle \alpha =\beta }
s
=
−
α
±
λ
{\displaystyle s=-\alpha \pm \lambda }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
s
=
−
α
±
j
ω
{\displaystyle s=-\alpha \pm j\omega }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
Nghiệm Phương Trình
i
(
t
)
=
A
e
s
t
{\displaystyle i(t)=Ae^{st}}
i
(
t
)
=
A
e
−
α
=
A
(
α
)
{\displaystyle i(t)=Ae^{-\alpha }=A(\alpha )}
i
(
t
)
=
A
e
(
−
α
±
λ
)
t
=
A
(
α
)
e
λ
t
+
A
(
α
)
e
−
λ
t
{\displaystyle i(t)=Ae^{(-\alpha \pm \lambda )t}=A(\alpha )e^{\lambda t}+A(\alpha )e^{-\lambda t}}
i
(
t
)
=
A
e
(
−
α
±
j
ω
)
t
=
A
(
α
)
s
i
n
ω
t
{\displaystyle i(t)=Ae^{(-\alpha \pm j\omega )t}=A(\alpha )sin\omega t}
α
=
R
2
L
{\displaystyle \alpha ={\frac {R}{2L}}}
β
=
1
L
C
{\displaystyle \beta ={\frac {1}{LC}}}
λ
=
α
−
β
{\displaystyle \lambda =\alpha -\beta }
ω
=
β
−
α
{\displaystyle \omega =\beta -\alpha }
Bộ phận điện tử cho điện ổn ở tần số thời gian
Bộ phận điện tử Lối mắc Tính chất
Bộ lọc tần số thấp
v
o
v
2
=
1
j
ω
C
R
+
1
j
ω
C
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {\frac {1}{j\omega C}}{R+{\frac {1}{j\omega C}}}}={\frac {1}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
=
1
R
C
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {1}{RC}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
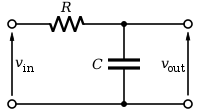
Bộ lọc tần số thấp
v
o
v
2
=
R
R
=
j
ω
L
=
1
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {R}{R=j\omega L}}={\frac {1}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
Bộ lọc tần số cao
v
o
v
2
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {j\omega T}{1+j\omega T}}}
T
=
R
C
{\displaystyle T=RC}
ω
o
=
1
T
=
1
R
C
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {1}{RC}}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ lọc tần số cao
v
o
v
2
=
j
ω
T
1
+
j
ω
T
{\displaystyle {\frac {v_{o}}{v_{2}}}={\frac {j\omega T}{1+j\omega T}}}
T
=
L
R
{\displaystyle T={\frac {L}{R}}}
ω
o
=
1
T
=
R
L
{\displaystyle \omega _{o}={\frac {1}{T}}={\frac {R}{L}}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
2
{\displaystyle v_{o}(\omega =\omega _{o})={\frac {v_{i}}{2}}}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ lọc băng tần
v
o
v
i
=
(
1
1
+
j
ω
T
L
)
(
j
ω
T
H
1
+
j
ω
H
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=({\frac {1}{1+j\omega T_{L}}})({\frac {j\omega T_{H}}{1+j\omega _{H}}})}
T
L
=
L
R
{\displaystyle T_{L}={\frac {L}{R}}}
T
H
=
R
C
{\displaystyle T_{H}=RC}
ω
L
−
ω
H
=
R
L
−
1
R
C
{\displaystyle \omega _{L}-\omega _{H}={\frac {R}{L}}-{\frac {1}{RC}}}
Bộ lọc băng tần
v
o
v
i
=
(
1
1
+
j
ω
T
L
)
(
j
ω
T
H
1
+
j
ω
H
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=({\frac {1}{1+j\omega T_{L}}})({\frac {j\omega T_{H}}{1+j\omega _{H}}})}
T
L
=
R
C
{\displaystyle T_{L}=RC}
T
H
=
L
R
{\displaystyle T_{H}={\frac {L}{R}}}
ω
L
−
ω
H
=
1
R
C
−
R
L
{\displaystyle \omega _{L}-\omega _{H}={\frac {1}{RC}}-{\frac {R}{L}}}
Bộ lọc băng tần chọn lựa
v
o
v
i
=
R
R
+
j
ω
L
+
1
j
ω
C
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega L+{\frac {1}{j\omega C}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
{\displaystyle v_{o}(\omega =\omega _{o})=v_{i}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
Bộ lọc băng tần chọn lựa
v
o
v
i
=
j
ω
C
+
1
j
ω
L
R
+
j
ω
C
+
1
j
ω
L
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega C+{\frac {1}{j\omega L}}}{R+j\omega C+{\frac {1}{j\omega L}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
0
{\displaystyle v_{o}(\omega =0)=0}
v
o
(
ω
=
ω
o
)
=
v
i
{\displaystyle v_{o}(\omega =\omega _{o})=v_{i}}
v
o
(
ω
=
00
)
=
0
{\displaystyle v_{o}(\omega =00)=0}
Bộ lọc băng tần chọn lược
v
o
v
i
=
R
R
+
j
ω
L
+
1
j
ω
C
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {R}{R+j\omega L+{\frac {1}{j\omega C}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
0
{\displaystyle v_{o}(\omega =\omega _{o})=0}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ lọc băng tần chọn lược
v
o
v
i
=
j
ω
C
+
1
j
ω
L
R
+
j
ω
C
+
1
j
ω
L
{\displaystyle {\frac {v_{o}}{v_{i}}}={\frac {j\omega C+{\frac {1}{j\omega L}}}{R+j\omega C+{\frac {1}{j\omega L}}}}}
ω
=
ω
1
−
ω
2
{\displaystyle \omega =\omega _{1}-\omega _{2}}
v
o
(
ω
=
0
)
=
v
i
{\displaystyle v_{o}(\omega =0)=v_{i}}
v
o
(
ω
=
ω
o
)
=
0
{\displaystyle v_{o}(\omega =\omega _{o})=0}
v
o
(
ω
=
00
)
=
v
i
{\displaystyle v_{o}(\omega =00)=v_{i}}
Bộ phận điện tử Khuếch đại điện âm Khuếch đại điện dương
Trăng si tơ
v
o
v
i
=
1
−
(
R
2
R
2
+
R
1
)
(
R
3
R
4
)
{\displaystyle {\frac {v_{o}}{v_{i}}}=1-({\frac {R_{2}}{R_{2}+R_{1}}})({\frac {R_{3}}{R_{4}}})}
R
1
=
0
{\displaystyle R_{1}=0}
R
4
=
(
n
+
1
)
R
3
{\displaystyle R_{4}=(n+1)R_{3}}
V
o
u
t
=
−
n
V
i
n
{\displaystyle V_{\mathrm {out} }=-nV_{\mathrm {in} }}
{\displaystyle }
Op amp 741
V
o
u
t
=
−
V
i
n
(
R
f
R
1
)
{\displaystyle V_{\mathrm {out} }=-V_{\mathrm {in} }\left({R_{f} \over R_{1}}\right)}
−
n
V
i
n
{\displaystyle -nV_{\mathrm {in} }}
R
f
=
n
R
1
{\displaystyle R_{f}=nR_{1}}
V
o
=
V
i
(
1
+
R
2
R
1
)
{\displaystyle V_{o}=V_{i}(1+{\frac {R_{2}}{R_{1}}})}
V
o
u
t
=
n
V
i
n
{\displaystyle V_{\mathrm {out} }=nV_{\mathrm {in} }}
R
2
=
n
R
1
{\displaystyle R_{2}=nR_{1}}
R
2
R
1
>>
1
{\displaystyle {\frac {R_{2}}{R_{1}}}>>1}
Biến điện
V
o
u
t
=
−
V
i
n
N
2
N
1
{\displaystyle V_{\mathrm {out} }=-V_{\mathrm {in} }{\frac {N_{2}}{N_{1}}}}
V
o
=
−
n
V
i
{\displaystyle V_{o}=-nV_{i}}
N
2
=
n
N
1
{\displaystyle N_{2}=nN_{1}}
V
o
u
t
=
V
i
n
N
2
N
1
{\displaystyle V_{\mathrm {out} }=V_{\mathrm {in} }{\frac {N_{2}}{N_{1}}}}
V
o
=
n
V
i
{\displaystyle V_{o}=nV_{i}}
N
2
=
n
N
1
{\displaystyle N_{2}=nN_{1}}
[ sửa ] Dao động điện được tìm thấy từ các mạch điện LC và RLC mắc nối tiếp
[ sửa ] Bộ phận điện tử biến đổi điện AC hai chiều thành điện AC một chiều
Bộ phận điện tử Tính chất
Với Biến điện chia ở trung tâm
Với Biến điện không có chia ở trung tâm
[ sửa ] Micro + Loa
Micro + Khuếch đại sóng âm + Loa Micro1 + Loa1
Micro2 + Loa2
De Morgan
P
⋅
Q
¯
=
P
¯
+
Q
¯
{\displaystyle {\overline {P\cdot Q}}={\overline {P}}+{\overline {Q}}}
P
+
Q
¯
=
P
¯
⋅
Q
¯
{\displaystyle {\overline {P+Q}}={\overline {P}}\cdot {\overline {Q}}}
Trao Đổi
A
+
(
B
+
C
)
=
(
A
+
B
)
+
C
{\displaystyle A+(B+C)=(A+B)+C}
A
⋅
(
B
+
C
)
=
(
A
+
B
)
⋅
C
{\displaystyle A\cdot (B+C)=(A+B)\cdot C}
Phân Phối
A
+
(
B
⋅
C
)
=
(
A
+
B
)
⋅
(
A
+
C
)
{\displaystyle A+(B\cdot C)=(A+B)\cdot (A+C)}
A
⋅
(
B
+
C
)
=
(
A
⋅
B
)
+
(
A
⋅
C
)
{\displaystyle A\cdot (B+C)=(A\cdot B)+(A\cdot C)}
Hoán Chuyển
A
⋅
B
{\displaystyle A\cdot B}
B
⋅
A
{\displaystyle B\cdot A}
A
+
B
{\displaystyle A+B}
B
+
A
{\displaystyle B+A}
Bao gồm các loại toán được thực hiện trên các Cổng số , Bộ phận điện số
Cổng Dẩn
Y
=
A
{\displaystyle Y=A}
Cổng NOT
Y
=
A
¯
{\displaystyle Y={\overline {A}}}
Cổng AND
Y
=
A
.
B
{\displaystyle Y=A.B}
Cổng OR
Y
=
A
+
B
{\displaystyle Y=A+B}
Cổng XOR
Y
=
A
+
B
{\displaystyle Y=A+B}
Cổng NAND
Y
=
A
.
B
¯
{\displaystyle Y={\overline {A.B}}}
Cổng NOR
Y
=
A
+
B
¯
=
A
¯
⋅
B
+
A
⋅
B
¯
¯
{\displaystyle Y={\overline {A+B}}={\overline {{{\overline {A}}\cdot B}+A\cdot {\overline {B}}}}}
Cổng XNOR
Y
=
A
+
B
¯
=
A
¯
⋅
B
+
A
⋅
B
¯
¯
{\displaystyle Y={\overline {A+B}}={\overline {{{\overline {A}}\cdot B}+A\cdot {\overline {B}}}}}
Cổng Dẩn
Y
=
A
¯
¯
=
A
{\displaystyle Y={\overline {\overline {A}}}=A}
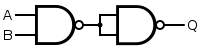
Cổng NAND
Y
=
A
.
A
¯
=
A
¯
{\displaystyle Y={\overline {A.A}}={\overline {A}}}
Y
1
=
A
.
A
¯
=
A
¯
{\displaystyle Y_{1}={\overline {A.A}}={\overline {A}}}
Y
2
=
B
.
B
¯
=
B
¯
{\displaystyle Y_{2}={\overline {B.B}}={\overline {B}}}
Y
=
Y
1
⋅
Y
2
¯
=
Y
1
+
Y
2
{\displaystyle Y={\overline {Y_{1}\cdot Y_{2}}}=Y_{1}+Y_{2}}
Ghép cổng chỉ dùng cổng NAND
Desired Gate
NAND Construction
Truth Table
Input A
Output Q
0
1
1
0
Desired Gate
NAND Construction
Truth Table
Input A
Input B
Output Q
0
0
0
0
1
0
1
0
0
1
1
1
Desired Gate
NAND Construction
Truth Table
Input A
Input B
Output Q
0
0
0
0
1
1
1
0
1
1
1
1
Desired Gate
NAND Construction
Truth Table
Input A
Input B
Output Q
0
0
1
0
1
0
1
0
0
1
1
0
Desired Gate
NAND Construction
Truth Table
Input A
Input B
Output Q
0
0
0
0
1
1
1
0
1
1
1
0
Desired Gate
NAND Construction
Truth Table
Input A
Input B
Output Q
0
0
1
0
1
0
1
0
0
1
1
1
[ sửa ] Số tử nhị phân bao gồm 2 con số 0 và 1
S
=
A
⊕
B
{\displaystyle {\mbox{S}}=A\oplus B}
C
=
A
B
{\displaystyle {\mbox{C}}=AB\,}
Bảng vận hành
A B S C
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
[ sửa ] Ký hiệu
Cấu tạo và lối hoạt động
S
=
(
A
⊕
B
)
⊕
C
i
n
{\displaystyle S=(A\oplus B)\oplus C_{in}}
C
o
u
t
=
(
A
⋅
B
)
+
(
C
i
n
⋅
(
A
⊕
B
)
)
{\displaystyle C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))}
Bảng vận hành
Input
Output
A
{\displaystyle A}
B
{\displaystyle B}
C
i
{\displaystyle C_{i}}
C
o
{\displaystyle C_{o}}
S
{\displaystyle S}
0
0
0
0
0
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
0
1
1
1
1
1
Dùng trong việc hiển thị số thập phân từ 0-9
a
b
c
d
e
f
g
Số thập phân
1
1
1
1
1
1
0
Số 0
a
b
c
d
e
f
g
Số 1
a
b
c
d
e
f
g
Số 2
a
b
c
d
e
f
g
Số 3
a
b
c
d
e
f
g
Số 4
a
b
c
d
e
f
g
Số 5
a
b
c
d
e
f
g
Số 6
a
b
c
d
e
f
g
Số 7
a
b
c
d
e
f
g
Số 8
a
b
c
d
e
f
g
Số 9
[ sửa ] Mả số nhị phân của số thập phân
A
B
a3
a2
a1
a0
Decimal Number
0
0
0
0
0
0
0
0
1
0
0
0
1
1
1
0
0
0
1
0
2
1
1
0
0
1
1
3
1
1
0
1
0
0
4
1
1
0
1
0
1
5
1
1
0
1
1
0
6
1
1
0
1
1
1
7
1
1
1
0
0
0
8
1
1
1
0
0
1
9
[ sửa ] Mả số tiêu chuẩn bắc mỹ dùng trong việc trao đổi thông tin
Number from 0 to 9
Capital A to Z
Common a to z
Binary
Oct Dec Hex Glyph
010 0000
040
32
20
space
010 0001
041
33
21
!
010 0010
042
34
22
"
010 0011
043
35
23
#
010 0100
044
36
24
$
010 0101
045
37
25
%
010 0110
046
38
26
&
010 0111
047
39
27
'
010 1000
050
40
28
(
010 1001
051
41
29
)
010 1010
052
42
2A
*
010 1011
053
43
2B
+
010 1100
054
44
2C
,
010 1101
055
45
2D
-
010 1110
056
46
2E
.
010 1111
057
47
2F
/
011 0000
060
48
30
0
011 0001
061
49
31
1
011 0010
062
50
32
2
011 0011
063
51
33
3
011 0100
064
52
34
4
011 0101
065
53
35
5
011 0110
066
54
36
6
011 0111
067
55
37
7
011 1000
070
56
38
8
011 1001
071
57
39
9
011 1010
072
58
3A
:
011 1011
073
59
3B
;
011 1100
074
60
3C
<
011 1101
075
61
3D
=
011 1110
076
62
3E
>
011 1111
077
63
3F
?
100 0000
100
64
40
@
100 0001
101
65
41
A
100 0010
102
66
42
B
100 0011
103
67
43
C
100 0100
104
68
44
D
100 0101
105
69
45
E
100 0110
106
70
46
F
100 0111
107
71
47
G
100 1000
110
72
48
H
100 1001
111
73
49
I
100 1010
112
74
4A
J
100 1011
113
75
4B
K
100 1100
114
76
4C
L
100 1101
115
77
4D
M
100 1110
116
78
4E
N
100 1111
117
79
4F
O
101 0000
120
80
50
P
101 0001
121
81
51
Q
101 0010
122
82
52
R
101 0011
123
83
53
S
101 0100
124
84
54
T
101 0101
125
85
55
U
101 0110
126
86
56
V
101 0111
127
87
57
W
101 1000
130
88
58
X
101 1001
131
89
59
Y
101 1010
132
90
5A
Z
101 1011
133
91
5B
[
101 1100
134
92
5C
\
101 1101
135
93
5D
]
101 1110
136
94
5E
^
101 1111
137
95
5F
_
110 0000
140
96
60
`
110 0001
141
97
61
a
110 0010
142
98
62
b
110 0011
143
99
63
c
110 0100
144
100
64
d
110 0101
145
101
65
e
110 0110
146
102
66
f
110 0111
147
103
67
g
110 1000
150
104
68
h
110 1001
151
105
69
i
110 1010
152
106
6A
j
110 1011
153
107
6B
k
110 1100
154
108
6C
l
110 1101
155
109
6D
m
110 1110
156
110
6E
n
110 1111
157
111
6F
o
111 0000
160
112
70
p
111 0001
161
113
71
q
111 0010
162
114
72
r
111 0011
163
115
73
s
111 0100
164
116
74
t
111 0101
165
117
75
u
111 0110
166
118
76
v
111 0111
167
119
77
w
111 1000
170
120
78
x
111 1001
171
121
79
y
111 1010
172
122
7A
z
111 1011
173
123
7B
{
111 1100
174
124
7C
|
111 1101
175
125
7D
}
111 1110
176
126
7E
~
[ sửa ] Bộ phận điện số dùng điều khiển để chọn lựa đường xuất
a
,
b
{\displaystyle a,b}
L
3
,
L
2
,
L
1
,
L
0
{\displaystyle L_{3},L_{2},L_{1},L_{0}}
Từ trên,
Với 2 điều khiển ở cổng nhập, ta có thể chọn lựa
2
2
=
4
{\displaystyle 2^{2}=4}
Với 3 điều khiển ở cổng nhập, ta có thể chọn lựa
2
3
=
8
{\displaystyle 2^{3}=8}
Với n điều khiển ở cổng nhập, ta có thể chọn lựa
2
n
{\displaystyle 2^{n}}
Bảng vận hành
a
b
L3
L2
L1
L0
Đường xuất được chọn
0
0
0
0
0
1
L0
0
1
0
0
1
0
L1
1
0
0
1
0
0
L2
1
1
1
0
0
0
L3
 --
--





 .
.
 .
.






































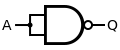



































![{\displaystyle P=P_{V}-P_{R}=iv-i^{2}R(T)=i[v-iR(T)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1de80c7acd662347367cbed760a299caa8e5091)