Định luật mạch điện

Định luật Kirchhoff

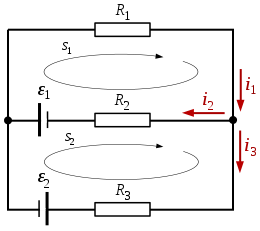
Định luật Kirchhoff được dùng để mô tả mối quan hệ của cường độ dòng điện và điện áp trong mạch điện. Các định luật này được Gustav Kirchhoff xây dựng vào năm 1845 bao gồm 2 định luật sau

Định luật Kirchhoff về cường độ dòng điện

Tổng giá trị đại số của dòng điện tại một nút trong một mạch điện là bằng không . Tại bất kỳ nút (ngã rẽ) nào trong một mạch điện, thì tổng cường độ dòng điện chạy đến nút phải bằng tổng cường độ dòng điện từ nút chạy đi
$\sum _{k=1}^{n}{I}_{k}=0$ . Với n là tổng số các nhánh với dòng điện chạy vào nút hay từ nút ra.
$\sum _{k=1}^{n}{\tilde {I}}_{k}=0$

Định luật Kirchhoff về điện thế

Tổng giá trị điện áp dọc theo một vòng bằng không
$\sum _{k=1}^{n}V_{k}=0$. Với n là tổng số các điện áp được đo.
$\sum _{k=1}^{n}{\tilde {V}}_{k}=0$

Thí dụ

Theo định luật 1, ta có:

$i_{1}-i_{2}-i_{3}=0\,$

Định luật 2 áp dụng cho vòng s₁:

$-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}=0$

Định luật 2 áp dụng cho vòng s₂:

$-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}=0$

Đến đây ta có hệ phương trình tuyến tính cho 3 ẩn số $i_{1},i_{2},i_{3}$:

${\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}&=0\\\end{cases}}$

Giả sử:

$R_{1}=100,\ R_{2}=200,\ R_{3}=300{\text{ (ohm)}};\ \epsilon _{1}=3,\ \epsilon _{2}=4{\text{ (volt)}}$

kết quả:

${\begin{cases}i_{1}={\frac {1}{1100}}{\text{ hay }}0.{\bar {90}}{\text{ mA}}\\i_{2}={\frac {4}{275}}{\text{ hay }}14.{\bar {54}}{\text{ mA}}\\i_{3}=-{\frac {3}{220}}{\text{ hay }}-13.{\bar {63}}{\text{ mA}}\\\end{cases}}$

$i_{3}$ mang dấu âm vì hướng của $i_{3}$ ngược với hướng giả định trong hình.

Định luật Norton

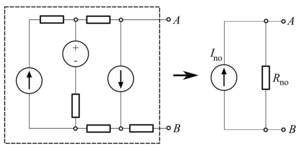
Mọi mạch điện đều có thể biểu diển bằng mạch điện tương đương của mạch điện song song của dòng điện nguồn và điên dần tổng sau

Định luật Thevenin

Mọi mạch điện đều có thể biểu diển bằng mạch điện nối tiếp của một điện thế và điện kháng như sau